Question
Consider the function \(f(x) = \frac{{\ln x}}{x}\) , \(0 < x < {{\text{e}}^2}\) .
(i) Solve the equation \(f'(x) = 0\) .
(ii) Hence show the graph of \(f\) has a local maximum.
(iii) Write down the range of the function \(f\) .
Show that there is a point of inflexion on the graph and determine its coordinates.
Sketch the graph of \(y = f(x)\) , indicating clearly the asymptote, x-intercept and the local maximum.
Now consider the functions \(g(x) = \frac{{\ln \left| x \right|}}{x}\) and \(h(x) = \frac{{\ln \left| x \right|}}{{\left| x \right|}}\) , where \(0 < x < {{\text{e}}^2}\) .
(i) Sketch the graph of \(y = g(x)\) .
(ii) Write down the range of \(g\) .
(iii) Find the values of \(x\) such that \(h(x) > g(x)\) .
Answer/Explanation
Markscheme
(i) \(f'(x) = \frac{{x\frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\)
so \(f'(x) = 0\) when \(\ln x = 1\), i.e. \(x = {\text{e}}\) A1
(ii) \(f'(x) > 0\) when \(x < {\text{e}}\) and \(f'(x) < 0\) when \(x > {\text{e}}\) R1
hence local maximum AG
Note: Accept argument using correct second derivative.
(iii) \(y \leqslant \frac{1}{{\text{e}}}\) A1
[5 marks]
\(f”(x) = \frac{{{x^2}\frac{{ – 1}}{x} – \left( {1 – \ln x} \right)2x}}{{{x^4}}}\) M1
\( = \frac{{ – x – 2x + 2x\ln x}}{{{x^4}}}\)
\( = \frac{{ – 3 + 2\ln x}}{{{x^3}}}\) A1
Note: May be seen in part (a).
\(f”(x) = 0\) (M1)
\({ – 3 + 2\ln x = 0}\)
\(x = {{\text{e}}^{\frac{3}{2}}}\)
since \(f”(x) < 0\) when \(x < {{\text{e}}^{\frac{3}{2}}}\) and \(f”(x) > 0\) when \(x > {{\text{e}}^{\frac{3}{2}}}\) R1
then point of inflexion \(\left( {{{\text{e}}^{\frac{3}{2}}},\frac{3}{{2{{\text{e}}^{\frac{3}{2}}}}}} \right)\) A1
[5 marks]
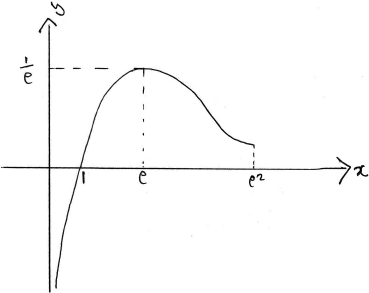A1A1A1
Note: Award A1 for the maximum and intercept, A1 for a vertical asymptote and A1 for shape (including turning concave up).
[3 marks]
(i)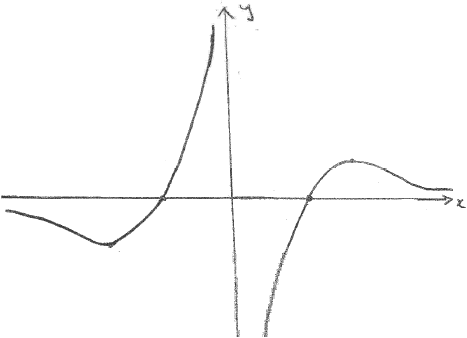
A1A1
Note: Award A1 for each correct branch.
(ii) all real values A1
(iii)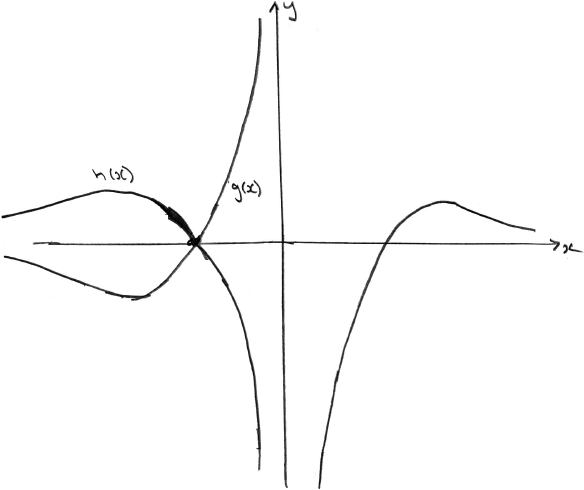
(M1)(A1)
Note: Award (M1)(A1) for sketching the graph of h, ignoring any graph of g.
\( – {{\text{e}}^2} < x < – 1\) (accept \(x < – 1\) ) A1
[6 marks]
Examiners report
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Question
Let \(f(x) = \sqrt {\frac{x}{{1 – x}}} ,{\text{ }}0 < x < 1\).
Show that \(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) and deduce that f is an increasing function.
Show that the curve \(y = f(x)\) has one point of inflexion, and find its coordinates.
Use the substitution \(x = {\sin ^2}\theta \) to show that \(\int {f(x){\text{d}}x} = \arcsin \sqrt x – \sqrt {x – {x^2}} + c\) .
Answer/Explanation
Markscheme
EITHER
derivative of \(\frac{x}{{1 – x}}\) is \(\frac{{(1 – x) – x( – 1)}}{{{{(1 – x)}^2}}}\) M1A1
\(f'(x) = \frac{1}{2}{\left( {\frac{x}{{1 – x}}} \right)^{ – \frac{1}{2}}}\frac{1}{{{{(1 – x)}^2}}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
OR
\(f(x) = \frac{{{x^{\frac{1}{2}}}}}{{{{(1 – x)}^{\frac{1}{2}}}}}\)
\(f'(x) = \frac{{{{(1 – x)}^{\frac{1}{2}}}\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \frac{1}{2}{x^{\frac{1}{2}}}{{(1 – x)}^{ – \frac{1}{2}}}( – 1)}}{{1 – x}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{1}{2}}} + \frac{1}{2}{x^{\frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}[1 – x + x]\) M1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
[5 marks]
\(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\)
\( \Rightarrow f”(x) = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{3}{2}}} + \frac{3}{4}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{5}{2}}}\) M1A1
\( = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{5}{2}}}[1 – 4x]\)
\(f”(x) = 0 \Rightarrow x = \frac{1}{4}\) M1A1
\(f”(x)\) changes sign at \(x = \frac{1}{4}\) hence there is a point of inflexion R1
\(x = \frac{1}{4} \Rightarrow y = \frac{1}{{\sqrt 3 }}\) A1
the coordinates are \(\left( {\frac{1}{4},\frac{1}{{\sqrt 3 }}} \right)\)
[6 marks]
\(x = {\sin ^2}\theta \Rightarrow \frac{{{\text{d}}x}}{{{\text{d}}\theta }} = 2\sin \theta \cos \theta \) M1A1
\(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \int {\sqrt {\frac{{{{\sin }^2}\theta }}{{1 – {{\sin }^2}\theta }}} 2\sin \theta \cos \theta {\text{d}}\theta } } \) M1A1
\( = \int {2{{\sin }^2}\theta {\text{d}}\theta } \) A1
\( = \int {1 – \cos 2\theta } {\text{d}}\theta \) M1A1
\( = \theta – \frac{1}{2}\sin 2\theta + c\) A1
\(\theta = \arcsin \sqrt x \) A1
\(\frac{1}{2}\sin 2\theta = \sin \theta \cos \theta = \sqrt x \sqrt {1 – x} = \sqrt {x – {x^2}} \) M1A1
hence \(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \arcsin \sqrt x } – \sqrt {x – {x^2}} + c\) AG
[11 marks]
Examiners report
Part (a) was generally well done, although few candidates made the final deduction asked for. Those that lost other marks in this part were generally due to mistakes in algebraic manipulation. In part (b) whilst many students found the second derivative and set it equal to zero, few then confirmed that it was a point of inflexion. There were several good attempts for part (c), even though there were various points throughout the question that provided stopping points for other candidates.
Part (a) was generally well done, although few candidates made the final deduction asked for. Those that lost other marks in this part were generally due to mistakes in algebraic manipulation. In part (b) whilst many students found the second derivative and set it equal to zero, few then confirmed that it was a point of inflexion. There were several good attempts for part (c), even though there were various points throughout the question that provided stopping points for other candidates.
Part (a) was generally well done, although few candidates made the final deduction asked for. Those that lost other marks in this part were generally due to mistakes in algebraic manipulation. In part (b) whilst many students found the second derivative and set it equal to zero, few then confirmed that it was a point of inflexion. There were several good attempts for part (c), even though there were various points throughout the question that provided stopping points for other candidates.