Question
A student investigating the relationship between chemical reactions and temperature finds
the Arrhenius equation on the internet.
\(k=Ae^{-\frac{c}{T}}\)
This equation links a variable k with the temperature T, where A and c are positive
constants and T > 0.
(a) Show that \(\frac{dk}{dT}\) is always positive. [3]
(b) Given that \(\lim_{T\rightarrow \infty }k=A \ and \ \lim_{T\rightarrow 0}k=0\), sketch the graph of k against T. [3]
The Arrhenius equation predicts that the graph of ln k against \(\frac{1}{T}\) is a straight line.
(c) Write down
(i) the gradient of this line in terms of c ;
(ii) the y-intercept of this line in terms of A. [4]
The following data are found for a particular reaction, where T is measured in Kelvin
and k is measured in cm3 mol−1 s−1:
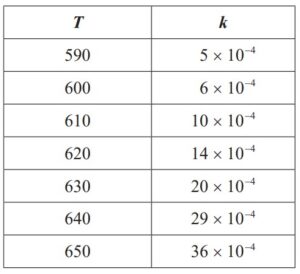
(d) Find the equation of the regression line for ln k on \(\frac{1}{T}\) [2]
(e) Find an estimate of
(i) c ;
(ii) A.
It is not required to state units for these values. [3]
▶️Answer/Explanation
Ans
4. (a) attempt to use chain rule, including the differentiation of \(\frac{1}{T}\) (M1)
\(\frac{dk}{dT}=A\times \frac{c}{T^{2}}\times e^{-\frac{c}{T}}\)
this is the product of positive quantities so must be positive R1
Note: The R1 may be awarded for correct argument from their derivative.
R1 is not possible if their derivative is not always positive.
[3 marks]
(b)
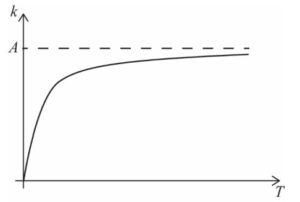
A1A1A1
Note: Award A1 for an increasing graph, entirely in first quadrant, becoming
concave down for larger values of T, A1 for tending towards the origin
and A1 for asymptote labelled at k = A .
[3 marks]
(c) taking ln of both sides OR substituting y = ln x and \(x=\frac{1}{T}\) (M1)
\(ln k=ln A=-\frac{c}{T}\ OR \ y=-cx+ln A\) (A1)
(i) so gradient is −c A1
(ii) y-intercept is ln A A1
Note: The implied (M1) and (A1) can only be awarded if both correct answers are
seen. Award zero if only one value is correct and no working is seen.
[4 marks]
continued…
(d) an attempt to convert data to \(\frac{1}{T}\) ln k (M1)
e.g. at least one correct row in the following table
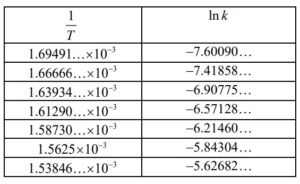
line is \(ln k=-13400\times \frac{1}{T}+15.0 \left ( =-13383.1…\times \frac{1}{T}+15.0107 \right )\) A1
[2 marks]
(e) (i) c =13400 (13383.1 ) … A1
(ii) attempt to rearrange or solve graphically ln 15.0107 A = … (M1)
A = (3300000 3304 258…) A1
Note: Accept an A value of 3269017… from use of 3sf value.
[3 marks]
Total [15 marks]
Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
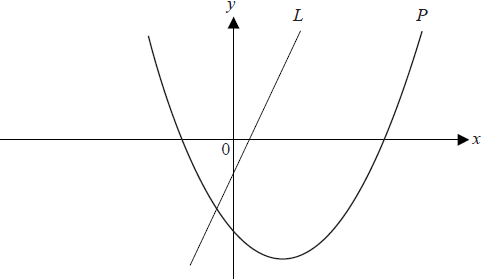
a.Find the gradient of the line L.[2]
b.Differentiate \(f (x)\) .[2]
c.Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
d.Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
e.Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
f.State the equation of the axis of symmetry of P.[1]
g.Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
▶️Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
a.Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
b.Write down the equation of the vertical asymptote.[2]
c.On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
d.Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
e.Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
f.The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
▶️Answer/Explanation
Markscheme
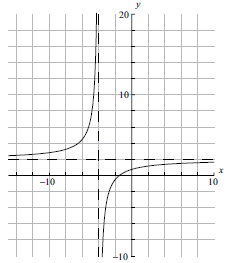(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
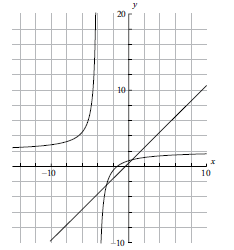(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
On the coordinate axes below, \({\text{D}}\) is a point on the \(y\)-axis and \({\text{E}}\) is a point on the \(x\)-axis. \({\text{O}}\) is the origin. The equation of the line \({\text{DE}}\) is \(y + \frac{1}{2}x = 4\).
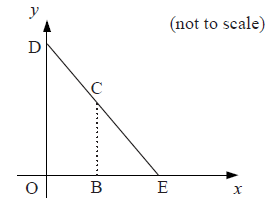
Write down the coordinates of point \({\text{E}}\).[2]
\({\text{C}}\) is a point on the line \({\text{DE}}\). \({\text{B}}\) is a point on the \(x\)-axis such that \({\text{BC}}\) is parallel to the \(y\)-axis. The \(x\)-coordinate of \({\text{C}}\) is \(t\).
Show that the \(y\)-coordinate of \({\text{C}}\) is \(4 – \frac{1}{2}t\).[2]
c.\({\text{OBCD}}\) is a trapezium. The \(y\)-coordinate of point \({\text{D}}\) is \(4\).
Show that the area of \({\text{OBCD}}\) is \(4t – \frac{1}{4}{t^2}\).[3]
d.The area of \({\text{OBCD}}\) is \(9.75\) square units. Write down a quadratic equation that expresses this information.[1]
e.(i) Using your graphic display calculator, or otherwise, find the two solutions to the quadratic equation written in part (d).
(ii) Hence find the correct value for \(t\). Give a reason for your answer.[4]
▶️Answer/Explanation
Markscheme
\({\text{E}}(8{\text{, }}0)\) (A1)(A1)
Notes: Brackets required but do not penalize again if mark lost in Q4 (i)(d). If missing award (A1)(A0).
Accept \(x = 8\), \(y = 0\)
Award (A1) for \(x = 8\)
\(y + \frac{1}{2}t = 4\) (M1)(M1)
Note: (M1) for the equation of the line seen. (M1) for substituting \(t\).
\(y = 4 – \frac{1}{2}t\) (AG)
Note: Final line must be seen or previous (M1) mark is lost.[2 marks]
\({\text{Area}} = \frac{1}{2} \times (4 + 4 – \frac{1}{2}t) \times t\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct substitution.
\( = \frac{1}{2} \times (8 – \frac{1}{2}t) \times t = \frac{1}{2}(8t – \frac{1}{2}{t^2})\) (A1)
\( = 4t – \frac{1}{4}{t^2}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[3 marks]
\(4t – \frac{1}{4}{t^2} = 9.75\) or any equivalent form. (A1)[1 mark]
(i) \(t = 3\) or \(t =13\) (A1)(ft)(A1)(ft)(G2)
Note: Follow through from candidate’s equation to part (d). Award (A0)(A1)(ft) for \((3{\text{, }}0)\) and \((13{\text{, }}0)\).
(ii) \(t\) must be a value between \(0\) and \(8\) then \(t = 3\)
Note: Accept \({\text{B}}\) is between \({\text{O}}\) and \({\text{E}}\). Do not award (R0)(A1).
Question
a.Consider the curve \(y = {x^3} + \frac{3}{2}{x^2} – 6x – 2\) .
(i) Write down the value of \(y\) when \(x\) is \(2\).
(ii) Write down the coordinates of the point where the curve intercepts the \(y\)-axis.[3]
b.Sketch the curve for \( – 4 \leqslant x \leqslant 3\) and \( – 10 \leqslant y \leqslant 10\). Indicate clearly the information found in (a).[4]
c.Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) .[3]
d.Let \({L_1}\) be the tangent to the curve at \(x = 2\).
Let \({L_2}\) be a tangent to the curve, parallel to \({L_1}\).
(i) Show that the gradient of \({L_1}\) is \(12\).
(ii) Find the \(x\)-coordinate of the point at which \({L_2}\) and the curve meet.
(iii) Sketch and label \({L_1}\) and \({L_2}\) on the diagram drawn in (b).[8]
e.It is known that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} > 0\) for \(x < – 2\) and \(x > b\) where \(b\) is positive.
(i) Using your graphic display calculator, or otherwise, find the value of \(b\).
(ii) Describe the behaviour of the curve in the interval \( – 2 < x < b\) .
(iii) Write down the equation of the tangent to the curve at \(x = – 2\).[5]
▶️Answer/Explanation
Markscheme
(i) \(y = 0\) (A1)
(ii) \((0{\text{, }}{- 2})\) (A1)(A1)
Note: Award (A1)(A0) if brackets missing.
OR
\(x = 0{\text{, }}y = – 2\) (A1)(A1)
Note: If coordinates reversed award (A0)(A1)(ft). Two coordinates must be given.[3 marks]
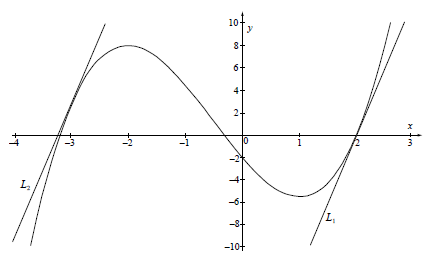(A4)
Notes: (A1) for appropriate window. Some indication of scale on the \(x\)-axis must be present (for example ticks). Labels not required. (A1) for smooth curve and shape, (A1) for maximum and minimum in approximately correct position, (A1) for \(x\) and \(y\) intercepts found in (a) in approximately correct position.[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 3{x^2} + 3x – 6\) (A1)(A1)(A1)
Note: (A1) for each correct term. Award (A1)(A1)(A0) at most if any other term is present.[3 marks]
(i) \(3 \times 4 + 3 \times 2 – 6 = 12\) (M1)(A1)(AG)
Note: (M1) for using the derivative and substituting \(x = 2\) . (A1) for correct (and clear) substitution. The \(12\) must be seen.
(ii) Gradient of \({L_2}\) is \(12\) (can be implied) (A1)
\(3{x^2} + 3x – 6 = 12\) (M1)
\(x = – 3\) (A1)(G2)
Note: (M1) for equating the derivative to \(12\) or showing a sketch of the derivative together with a line at \(y = 12\) or a table of values showing the \(12\) in the derivative column.
(iii) (A1) for \({L_1}\) correctly drawn at approx the correct point (A1)
(A1) for \({L_2}\) correctly drawn at approx the correct point (A1)
(A1) for 2 parallel lines (A1)
Note: If lines are not labelled award at most (A1)(A1)(A0). Do not accept 2 horizontal or 2 vertical parallel lines.[8 marks]
(i) \(b = 1\) (G2)
(ii) The curve is decreasing. (A1)
Note: Accept any valid description.
(iii) \(y = 8\) (A1)(A1)(G2)
Note: (A1) for “\(y =\) a constant”, (A1) for \(8\).[5 marks]