Question 3. [Maximum mark: 15]
A hollow chocolate box is manufactured in the form of a right prism with a regular hexagonal base. The height of the prism is h cm, and the top and base of the prism have sides of length x cm.
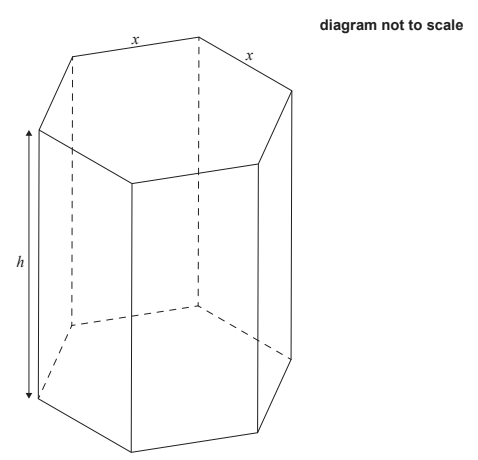
a. Given that \(sin 60\frac{\sqrt{3}}{2}\) show that the area of the base of the box is equal to \(\frac{3\sqrt{3x^{2}}}{2}\) [2]
b. Given that the total external surface area of the box is 1200 cm2, show that the volume of the box may be expressed as V = 300 \(\sqrt{3x}-\frac{9}{4}x^{3}\) [5]
c. Sketch the graph of V = 300 \(\sqrt{3x}-\frac{9}{4}x^{3}\) for 0 ≤ x ≤ 16. [2]
d. Find an expression for \(\frac{dV}{dx}\) . [2]
e. Find the value of x which maximizes the volume of the box. [2]
f. Hence, or otherwise, find the maximum possible volume of the box. [2]
▶️Answer/Explanation
(a) splitting diagram into equilateral triangles area \(= 6(\frac{1}{2}x^{2}sin60)\)
\(=\frac{3\sqrt{3}x^{2}}{2}\)
(b) total surface area of prism
\(1200= 2 (3x^{2}\frac{\sqrt{3}}{2})+6xh\)
\(h= \frac{400-\sqrt{3x^{2}}}{2x}\)
\(volume of prism =\frac{3\sqrt{3}}{2}x^{2}h\)
\(= \frac{3\sqrt{3}}{2}x^{2}(\frac{400-\sqrt{3x^{2}}}{2x})
\(= 300\sqrt{3x}-\frac{9}{4}x^{3}\)
(c)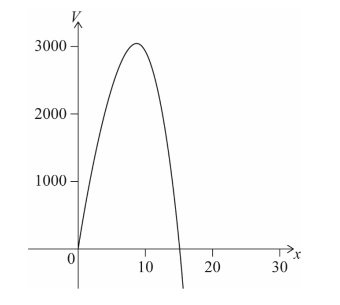 
(d)\(\frac{dV}{dx}= 300\sqrt{3}-\frac{27}{4}x^{2}\)
(e) from the graph of V or\(\frac{dV}{dx}OR solving \frac{dV}{dx}= 0\) \( x = 8.77 (8.77382…)\)
(f) from the graph of V OR substituting their value for x into V
\(V_{max}= 3040 cm^{2}\rightarrow (3039.34…)\)
Question 4. [Maximum mark: 14]
Charlotte decides to model the shape of a cupcake to calculate its volume.
From rotating a photograph of her cupcake she estimates that its cross-section passes through the points (0 , 3.5), (4 , 6), (6.5 , 4), (7 , 3) and (7.5 , 0), where all units are in centimetres. The cross-section is symmetrical in the x-axis, as shown below:
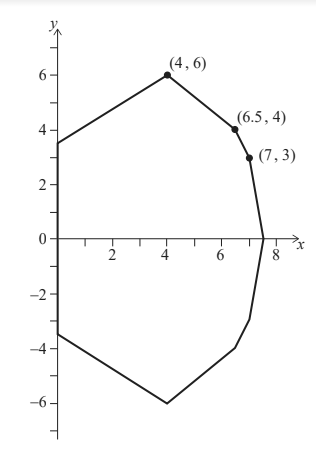
She models the section from (0 , 3.5) to (4 , 6) as a straight line.
a. Find the equation of the line passing through these two points. [2]
Charlotte models the section of the cupcake that passes through the points (4 , 6), (6.5 , 4), (7 , 3) and (7.5 , 0) with a quadratic curve.
b.(i) Find the equation of the least squares regression quadratic curve for these four points.
b. (ii) By considering the gradient of this curve when x = 4 , explain why it may not be a good model. [3]
Charlotte thinks that a quadratic with a maximum point at (4 , 6) and that passes through the point (7.5 , 0) would be a better fit.
c. Find the equation of the new model. [4]
Believing this to be a better model for her cupcake, Charlotte finds the volume of revolution about the x-axis to estimate the volume of the cupcake.
d. (i) Write down an expression for her estimate of the volume as a sum of two integrals.
d. (ii) Find the value of Charlotte’s estimate. [5]
▶️Answer/Explanation
(a) \(y = \frac{5}{8}x+ \frac{7}{2}(y = 0.625x+ 3.5)\)
(b)(i) \(y= -0.975x^{2}+9.5x-16.7\)
\(y= -0974630x^{2}+9.55919x- 16.6569..)\)
(ii) gradient of curve is positive at x = 4
(c) let \(y=ax^{2}+bx+c\) differentiating or using \(x=\frac{-b}{2a}8a+b=0\) substituting in the coordinates
\(7.5^{2}a+ 7.5b+c=0
\(4^{2}a+ 4b+ c=6\)
solve to get \( y =-\frac{24}{49}x^{2}+\frac{192}{49}x-\frac{90}{49}\) OR
\(y = -0.490x^{2}+3.92x-1.84\)
(d)(i) \(\pi \int ^{4}_{0}(\frac{5}{8}x+3.5)^{2}dx+\pi \int ^{7.5}_{4}(-\frac{24}{49}(x-4^{2})+6)^{2}dx\)
(ii) 501cm3(501.189…)
Question
Given \(f (x) = x^2 − 3x^{−1}, x \in {\mathbb{R}}, – 5 \leqslant x \leqslant 5, x \ne 0\),
A football is kicked from a point A (a, 0), 0 < a < 10 on the ground towards a goal to the right of A.
The ball follows a path that can be modelled by part of the graph
\(y = − 0.021x^2 + 1.245x − 6.01, x \in {\mathbb{R}}, y \geqslant 0\).
x is the horizontal distance of the ball from the origin
y is the height above the ground
Both x and y are measured in metres.
i.a.Write down the equation of the vertical asymptote.[1]
i.b.Find \(f ′(x)\).[2]
i.c.Using your graphic display calculator or otherwise, write down the coordinates of any point where the graph of \(y = f (x)\) has zero gradient.[2]
i.d.Write down all intervals in the given domain for which \(f (x)\) is increasing.[3]
ii.a.Using your graphic display calculator or otherwise, find the value of a.[1]
ii.b.Find \(\frac{{dy}}{{dx}}\).[2]
ii.c.(i) Use your answer to part (b) to calculate the horizontal distance the ball has travelled from A when its height is a maximum.
(ii) Find the maximum vertical height reached by the football.[4]
ii.d.Draw a graph showing the path of the football from the point where it is kicked to the point where it hits the ground again. Use 1 cm to represent 5 m on the horizontal axis and 1 cm to represent 2 m on the vertical scale.[4]
ii.e.The goal posts are 35 m from the point where the ball is kicked.
At what height does the ball pass over the goal posts?[2]
▶️Answer/Explanation
Markscheme
equation of asymptote is x = 0 (A1)
(Must be an equation.)[1 mark]
\(f ‘(x) = 2x + 3x^{-2}\) (or equivalent) (A1) for each term (A1)(A1)[2 marks]
stationary point (–1.14, 3.93) (G1)(G1)(ft)
(-1,4) or similar error is awarded (G0)(G1)(ft). Here and also as follow through in part (d) accept exact values \( – {\left( {\frac{3}{2}} \right)^{\frac{1}{3}}}\)for the x coordinate and \(3{\left( {\frac{3}{2}} \right)^{\frac{2}{3}}}\) for the y coordinate.
OR \(2x + \frac{3}{{{x^2}}} = 0\) or equivalent
Correct coordinates as above (M1)
Follow through from candidate’s \(f ′(x)\). (A1)(ft)[2 marks]
In all alternative answers for (d), follow through from candidate’s x coordinate in part (c).
Alternative answers include:
–1.14 ≤ x < 0, 0 < x < 5 (A1)(A1)(ft)(A1)
OR [–1.14,0), (0,5)
Accept alternative bracket notation for open interval ] [. (Union of these sets is not correct, award (A2) if all else is right in this case.)
OR \( – 1.14 \leqslant x < 5,x \ne 0\)
In all versions 0 must be excluded (A1). -1.14 must be the left bound . 5 must be the right bound (A1). For \(x \geqslant – 1.14\) or \(x > – 1.14\) alone, award (A1). For \( – 1.4 \leqslant x < 0\) together with \(x > 0\) award (A2).[3 marks]
a = 5.30 (3sf) (Allow (5.30, 0) but 5.3 receives an (AP).) (A1)[1 mark]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.042x + 1.245\) (A1) for each term. (A1)(A1)[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) Maximum value when \(f ‘ (x) = 0\), \( – 0.042x + 1.245 = 0\), (M1)
(M1) is for either of the above but at least one must be seen.
(x = 29.6.)
Football has travelled 29.6 – 5.30 = 24.3 m (3sf) horizontally. (A1)(ft)
For answer of 24.3 m with no working or for correct subtraction of 5.3 from candidate’s x-coordinate at the maximum (if not 29.6), award (A1)(d).(UP) (ii) Maximum vertical height, f (29.6) = 12.4 m (M1)(A1)(ft)(G2)
(M1) is for substitution into f of a value seen in part (c)(i). f(24.3) with or without evaluation is awarded (M1)(A0). For any other value without working, award (G0). If lines are seen on the graph in part (d) award (M1) and then (A1) for candidate’s value \( \pm 0.5\) (3sf not required.)[4 marks]
(not to scale)
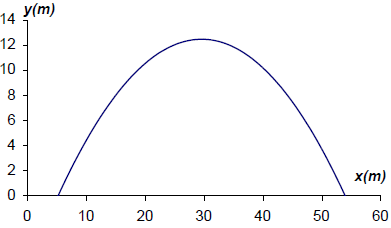(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for labels (units not required) and scale, (A1)(ft) for max(29.6,12.4), (A1)(ft) for x-intercepts at 5.30 and 53.9, (all coordinates can be within 0.5), (A1) for well-drawn parabola ending at the x-intercepts.[4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) f (40.3) = 10.1 m (3sf).
Follow through from (a). If graph used, award (M1) for lines drawn and (A1) for candidate’s value \( \pm 0.5\). (3sf not required). (M1)(A1)(ft)(G2)[2 marks]
Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
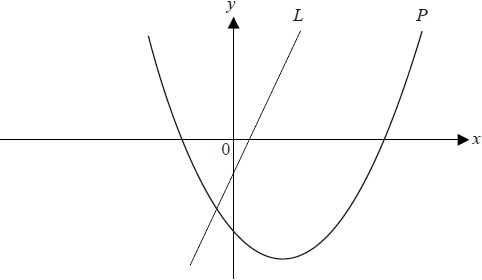
a.Find the gradient of the line L.[2]
b.Differentiate \(f (x)\) .[2]
c.Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
d.Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
e.Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
f.State the equation of the axis of symmetry of P.[1]
g.Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
▶️Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
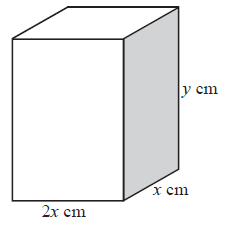
A closed rectangular box has a height \(y{\text{ cm}}\) and width \(x{\text{ cm}}\). Its length is twice its width. It has a fixed outer surface area of \(300{\text{ c}}{{\text{m}}^2}\) .
i.a.Factorise \(3{x^2} + 13x – 10\).[2]
i.b.Solve the equation \(3{x^2} + 13x – 10 = 0\).[2]
i.c.Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Find the equation of the axis of symmetry on the graph of this function.[2]
i.d.Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Calculate the minimum value of this function.[2]
ii.a.Show that \(4{x^2} + 6xy = 300\).[2]
ii.b.Find an expression for \(y\) in terms of \(x\).[2]
ii.c.Hence show that the volume \(V\) of the box is given by \(V = 100x – \frac{4}{3}{x^3}\).[2]
ii.d.Find \(\frac{{{\text{d}}V}}{{{\text{d}}x}}\).[2]
ii.e.(i) Hence find the value of \(x\) and of \(y\) required to make the volume of the box a maximum.
(ii) Calculate the maximum volume.[5]
▶️Answer/Explanation
Markscheme
\((3x – 2)(x + 5)\) (A1)(A1)[2 marks]
\((3x – 2)(x + 5) = 0\)
\(x = \frac{2}{3}\) or \(x = – 5\) (A1)(ft)(A1)(ft)(G2)[2 marks]
\(x = \frac{{ – 13}}{6}{\text{ }}( – 2.17)\) (A1)(A1)(ft)(G2)
Note: (A1) is for \(x = \), (A1) for value. (ft) if value is half way between roots in (b).[2 marks]
Minimum \(y = 3{\left( {\frac{{ – 13}}{6}} \right)^2} + 13\left( {\frac{{ – 13}}{6}} \right) – 10\) (M1)
Note: (M1) for substituting their value of \(x\) from (c) into \(f(x)\) .
\( = – 24.1\) (A1)(ft)(G2)[2 marks]
\({\text{Area}} = 2(2x)x + 2xy + 2(2x)y\) (M1)(A1)
Note: (M1) for using the correct surface area formula (which can be implied if numbers in the correct place). (A1) for using correct numbers.
\(300 = 4{x^2} + 6xy\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(6xy = 300 – 4{x^2}\) (M1)
\(y = \frac{{300 – 4{x^2}}}{{6x}}\) or \(\frac{{150 – 2{x^2}}}{{3x}}\) (A1)[2 marks]
\({\text{Volume}} = x(2x)y\) (M1)
\(V = 2{x^2}\left( {\frac{{300 – 4{x^2}}}{{6x}}} \right)\) (A1)(ft)
\( = 100x – \frac{4}{3}{x^3}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 100 – \frac{{12{x^2}}}{3}\) or \(100 – 4{x^2}\) (A1)(A1)
Note: (A1) for each term.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column
(i) For maximum \(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) or \(100 – 4{x^2} = 0\) (M1)
\(x = 5\) (A1)(ft)
\(y = \frac{{300 – 4{{(5)}^2}}}{{6(5)}}\) or \(\left( {\frac{{150 – 2{{(5)}^2}}}{{3(5)}}} \right)\) (M1)
\( = \frac{{20}}{3}\) (A1)(ft)
(UP) (ii) \(333\frac{1}{3}{\text{ c}}{{\text{m}}^3}{\text{ }}(333{\text{ c}}{{\text{m}}^3})\)
Note: (ft) from their (e)(i) if working for volume is seen.[5 marks]