Question
The diagram shows a pyramid \({\text{VABCD}}\) which has a square base of length \(10{\text{ cm}}\) and edges of length \(13{\text{ cm}}\). \({\text{M}}\) is the midpoint of the side \({\text{BC}}\).
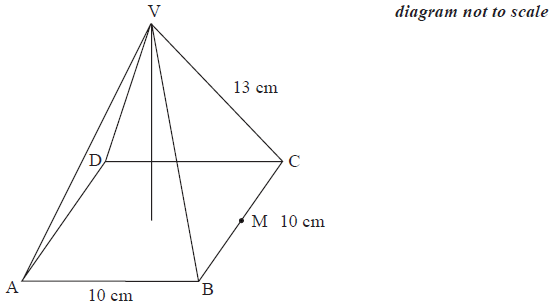
Calculate the length of \({\text{VM}}\).[2]
Calculate the vertical height of the pyramid.[2]
Answer/Explanation
Markscheme
Unit penalty (UP) applies in this question.
\({\text{VM}}^{2} = {13^2} – {5^2}\) (M1)
UP \( = 12{\text{ cm}}\) (A1) (C2)[2 marks]
Unit penalty (UP) applies in this question.
\({h^2} = {12^2} – {5^2}\) (or equivalent) (M1)
UP \( = 10.9{\text{ cm}}\) (A1)(ft) (C2)[2 marks]
Question
The right pyramid shown in the diagram has a square base with sides of length 40 cm. The height of the pyramid is also 40 cm.
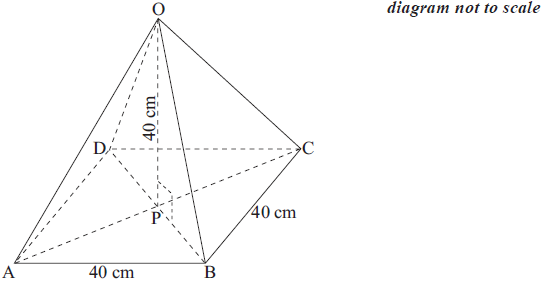
Find the length of OB.[4]
Find the size of angle OBP.[2]
Answer/Explanation
Markscheme
Note: Unit penalty (UP) applies in this part
\({\rm{PB}} = \frac{1}{2}\sqrt {{{40}^2} + {{40}^2}} = \sqrt {800} = 28.28(28.3)\) (M1)(A1)
Note: Award (M1) for correct substitutions, (A1) for correct answer.
(UP) \({\rm{OB}} = \sqrt {{{40}^2} + {{28.28}^2}} = 49.0{\text{ cm }}\left( {\sqrt {2400} {\text{ cm}}} \right)\) (M1)(A1)(ft) (C4)
Note: Award (M1) for correct substitution, can (ft) from any answer to PB.[4 marks]
\({\sin ^{ – 1}}\left( {\frac{{40}}{{49}}} \right)\)
OR
\({\cos ^{ – 1}}\left( {\frac{{28.28}}{{49}}} \right)\)
OR
\({\tan ^{ – 1}}\left( {\frac{{40}}{{28.28}}} \right)\) (M1)
= 54.7 (54.8) (A1)(ft) (C2)
Note: Award (M1) for any correct trig. ratio.
In radians = 0.616, award (M1)(A0).
Note: Common error: (a) \(OB = \sqrt {40^2 + 20^2} = 44.7 {\text{ cm}}\). Award (M0)(A0)(M1), (A1)(ft), and (b) angle OBP = 63.4° (63.5°) (M1)(A1)(ft).[2 marks]
Question
A shipping container is a cuboid with dimensions \({\text{16 m}}\), \({\text{1}}\frac{{\text{3}}}{{\text{4}}}{\text{ m}}\) and \({\text{2}}\frac{{\text{2}}}{{\text{3}}}{\text{ m}}\).
Calculate the exact volume of the container. Give your answer as a fraction.[3]
Jim estimates the dimensions of the container as 15 m, 2 m and 3 m and uses these to estimate the volume of the container.
Calculate the percentage error in Jim’s estimated volume of the container.[3]
Answer/Explanation
Markscheme
\(V = 16 \times 1\frac{3}{4} \times 2\frac{2}{3}\) (M1)
Note: Award (M1) for correct substitution in volume formula. Accept decimal substitution of \(2.66\) or better.
\( = 74.6666{\text{ }} \ldots \) (A1)
\( = {\text{74}}\frac{{\text{2}}}{{\text{3}}}{\text{ }}{{\text{m}}^{\text{3}}}{\text{ }}\left( {\frac{{{\text{224}}}}{{\text{3}}}{\text{ }}{{\text{m}}^{\text{3}}}} \right)\) (A1) (C3)
Note: Correct answer only.[3 marks]
\({\text{% error}} = \frac{{\left( {90 – 74\frac{2}{3}} \right) \times 100}}{{74\frac{2}{3}}}\) (A1)(M1)
Note: Award (A1) for \(90\) seen, or inferred in numerator, (M1) for correct substitution into percentage error formula.
\( = 20.5\) (A1)(ft) (C3)
Note: Accept \( – 20.5\).[3 marks]
Question
A rectangular cuboid has the following dimensions.
Length 0.80 metres (AD)
Width 0.50 metres (DG)
Height 1.80 metres (DC)
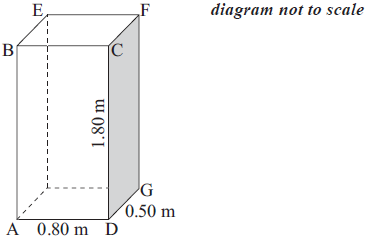
Calculate the length of AG.[2]
Calculate the length of AF.[2]
Find the size of the angle between AF and AG.[2]
Answer/Explanation
Markscheme
\({\text{AG}} = \sqrt {{{0.8}^2} + {{0.5}^2}} \) (M1)
AG = 0.943 m (A1) (C2)[2 marks]
\({\text{AF}} = \sqrt {{\text{A}}{{\text{G}}^2} + {{1.80}^2}} \) (M1)
= 2.03 m (A1)(ft) (C2)
Note: Follow through from their answer to part (a).[2 marks]
\(\cos {\rm{G\hat AF}} = \frac{{0.943(39 \ldots )}}{{2.03(22 \ldots )}}\) (M1)
\(\operatorname{G\hat AF} = 62.3^\circ \) (A1)(ft) (C2)
Notes: Award (M1) for substitution into correct trig ratio.
Accept alternative ratios which give 62.4° or 62.5°.
Follow through from their answers to parts (a) and (b).[2 marks]
Question
A room is in the shape of a cuboid. Its floor measures \(7.2\) m by \(9.6\) m and its height is \(3.5\) m.
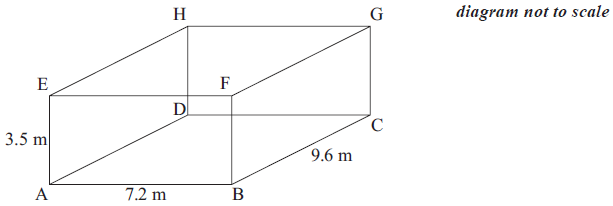
Calculate the length of AC.[2]
Calculate the length of AG.[2]
Calculate the angle that AG makes with the floor.[2]
Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {7.2^2} + {9.6^2}\) (M1)
Note: Award (M1) for correct substitution in Pythagoras Theorem.
\({\text{AC}} = 12{\text{ m}}\) (A1) (C2)[2 marks]
\({\text{A}}{{\text{G}}^2} = {12^2} + {3.5^2}\) (M1)
Note: Award (M1) for correct substitution in Pythagoras Theorem.
\({\text{AG}} = 12.5{\text{ m}}\) (A1)(ft) (C2)
Note: Follow through from their answer to part (a).[2 marks]
\(\tan \theta = \frac{{3.5}}{{12}}\) or \(\sin \theta = \frac{{3.5}}{{12.5}}\) or \(\cos \theta = \frac{{12}}{{12.5}}\) (M1)
Note: Award (M1) for correct substitutions in trig ratio.
\(\theta = {16.3^ \circ }\) (A1)(ft) (C2)
Notes: Follow through from parts (a) and/or part (b) where appropriate. Award (M1)(A0) for use of radians (0.284).[2 marks]
