Question
The scores of the eight highest scoring countries in the 2019 Eurovision song contest are
shown in the following table.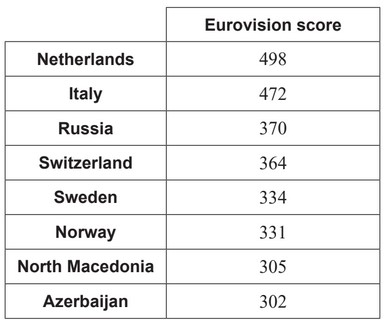
(a) For this data, find
(i) the upper quartile.
(ii) the interquartile range.
(b) Determine if the Netherlands’ score is an outlier for this data. Justify your answer.
Chester is investigating the relationship between the highest-scoring countries’ Eurovision
score and their population size to determine whether population size can reasonably be
used to predict a country’s score.
The populations of the countries, to the nearest million, are shown in the table.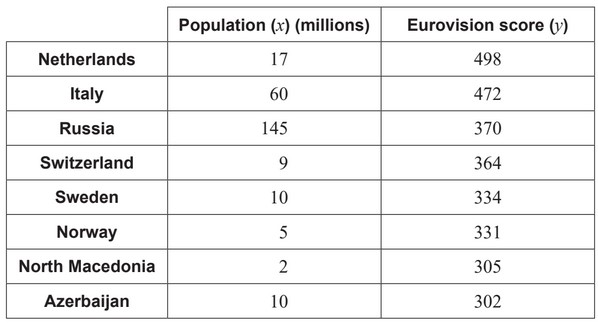
Chester finds that, for this data, the Pearson’s product moment correlation coefficient
is r = 0.249.
(c) State whether it would be appropriate for Chester to use the equation of a regression
line for y on x to predict a country’s Eurovision score. Justify your answer.
Chester then decides to find the Spearman’s rank correlation coefficient for this data,
and creates a table of ranks.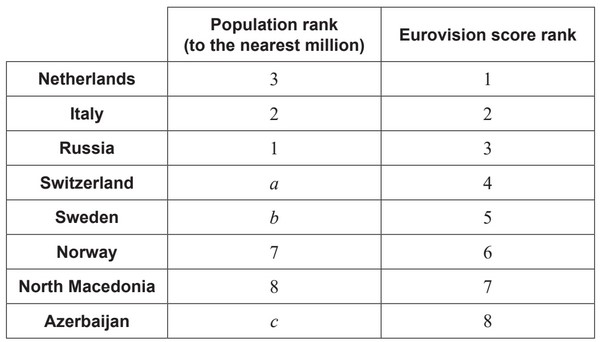
(d) Write down the value of:
(i) a ,
(ii) b ,
(iii) c .
(e) Find the value of the Spearman’s rank correlation coefficient \(r_s\).
(ii) Interpret the value obtained for \(r_S\).
(f) When calculating the ranks, Chester incorrectly read the Netherlands’ score as 478. Explain why the value of the Spearman’s rank correlation \(r_S\) does not change despite this error.
▶️Answer/Explanation
Ans:
(a) (i) \(\frac{370+472}{2}\)
\(Q_3 = 421\)
(ii) their part (a)(i) – their \(Q_1\) (clearly stated)
IQR = (421 – 318=) 103
(b) \((Q_3 + 1.5(IQR)=) 421 + (1.5 \(\times 103)\)
= 575.5
since 498 < 575.5
Netherlands is not an outlier
(c) not apptopriate (“no” no sufficient)
as r is too close to zero / too weak a correlation
(d) (i) 6
(ii) 4.5
(iii)4.5
(e) (i) \(r_s = 0.683 (0.682646…)\)
(ii) EITHER
there is a (positive) association between the population size and the score
OR
there is a (positive) linear correlation between the ranks of the population size
and the ranks of the scores (when compared with the PMCC of 0.249)
(f) lowering the top score by 20 does not change its rank so \(r_S\) is unchanged.
Question
Daniel grows apples and chooses at random a sample of 100 apples from his harvest.
a.He measures the diameters of the apples to the nearest cm. The following table shows the distribution of the diameters.

Using your graphic display calculator, write down the value of
(i) the mean of the diameters in this sample;
(ii) the standard deviation of the diameters in this sample.[3]
b.Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.
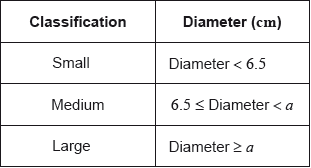
Calculate the percentage of small apples in Daniel’s harvest.[3]
c.Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.

Of the apples harvested, 5% are large apples.
Find the value of \(a\).[2]
d.Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.

Find the percentage of medium apples.[2]
e.Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.

This year, Daniel estimates that he will grow \({\text{100}}\,{\text{000}}\) apples.
Estimate the number of large apples that Daniel will grow this year.[2]
▶️Answer/Explanation
Markscheme
(i) \(6.76{\text{ (cm)}}\) (G2)
Notes: Award (M1) for an attempt to use the formula for the mean with a least two rows from the table.
(ii) \(1.14{\text{ (cm)}}\;\;\;\left( {1.14122 \ldots {\text{ (cm)}}} \right)\) (G1)
\({\text{P}}({\text{diameter}} < 6.5) = 0.338\;\;\;(0.338461)\) (M1)(A1)
Notes: Award (M1) for attempting to use the normal distribution to find the probability or for correct region indicated on labelled diagram. Award (A1) for correct probability.
\(33.8(\% )\) (A1)(ft)(G3)
Notes: Award (A1)(ft) for converting their probability into a percentage.
\({\text{P}}({\text{diameter}} \geqslant a) = 0.05\) (M1)
Note: Award (M1) for attempting to use the normal distribution to find the probability or for correct region indicated on labelled diagram.
\(a = 8.97{\text{ (cm)}}\;\;\;(8.97382 \ldots )\) (A1)(G2)
\(100 – (5 + 33.8461 \ldots )\) (M1)
Note: Award (M1) for subtracting “\(5+\) their part (b)” from 100 or (M1) for attempting to use the normal distribution to find the probability \({\text{P}}\left( {6.5 \leqslant {\text{diameter}} < {\text{their part (c)}}} \right)\) or for correct region indicated on labelled diagram.
\( = 61.2(\% )\;\;\;\left( {61.1538 \ldots (\% )} \right)\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b). Percentage symbol is not required. Accept \(61.1(\%)\) (\(61.1209\ldots(\%)\)) if \(8.97\) used.
\(100\,000 \times 0.05\) (M1)
Note: Award (M1) for multiplying by \(0.05\) (or \(5\%\)).
\( = 5000\) (A1)(G2)
Question
On one day 180 flights arrived at a particular airport. The distance travelled and the arrival status for each incoming flight was recorded. The flight was then classified as on time, slightly delayed, or heavily delayed.
The results are shown in the following table.
A χ2 test is carried out at the 10 % significance level to determine whether the arrival status of incoming flights is independent of the distance travelled.
The critical value for this test is 7.779.
A flight is chosen at random from the 180 recorded flights.
a.State the alternative hypothesis.[1]
b.Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.[2]
c.Write down the number of degrees of freedom.[1]
d.i.Write down the χ2 statistic.[2]
d.ii.Write down the associated p-value.[1]
e.State, with a reason, whether you would reject the null hypothesis.[2]
f.Write down the probability that this flight arrived on time.[2]
g.Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.[2]
h.Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.[3]
▶️Answer/Explanation
Markscheme
The arrival status is dependent on the distance travelled by the incoming flight (A1)
Note: Accept “associated” or “not independent”.[1 mark]
\(\frac{{60 \times 45}}{{180}}\) OR \(\frac{{60}}{{180}} \times \frac{{45}}{{180}} \times 180\) (M1)
Note: Award (M1) for correct substitution into expected value formula.
= 15 (A1) (G2)[2 marks]
4 (A1)
Note: Award (A0) if “2 + 2 = 4” is seen.[1 mark]
9.55 (9.54671…) (G2)
Note: Award (G1) for an answer of 9.54.[2 marks]
0.0488 (0.0487961…) (G1)[1 mark]
Reject the Null Hypothesis (A1)(ft)
Note: Follow through from their hypothesis in part (a).
9.55 (9.54671…) > 7.779 (R1)(ft)
OR
0.0488 (0.0487961…) < 0.1 (R1)(ft)
Note: Do not award (A1)(ft)(R0)(ft). Follow through from part (d). Award (R1)(ft) for a correct comparison, (A1)(ft) for a consistent conclusion with the answers to parts (a) and (d). Award (R1)(ft) for χ2calc > χ2crit , provided the calculated value is explicitly seen in part (d)(i).[2 marks]
\(\frac{{52}}{{180}}\,\,\left( {0.289,\,\,\frac{{13}}{{45}},\,\,28.9\,{\text{% }}} \right)\) (A1)(A1) (G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.[2 marks]
\(\frac{{35}}{{97}}\,\,\left( {0.361,\,\,36.1\,{\text{% }}} \right)\) (A1)(A1) (G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.[2 marks]
\(\frac{{14}}{{45}} \times \frac{{13}}{{44}}\) (A1)(M1)
Note: Award (A1) for two correct fractions and (M1) for multiplying their two fractions.
\( = \frac{{182}}{{1980}}\,\,\left( {0.0919,\,\,\frac{{91}}{{990}},\,0.091919 \ldots ,\,9.19\,{\text{% }}} \right)\) (A1) (G2)[3 marks]
Question
The lengths (\(l\)) in centimetres of \(100\) copper pipes at a local building supplier were measured. The results are listed in the table below.
a.Write down the mode.[1]
b.Using your graphic display calculator, write down the value of
(i) the mean;
(ii) the standard deviation;
(iii) the median.[4]
c.Find the interquartile range.[2]
d.Draw a box and whisker diagram for this data, on graph paper, using a scale of \(1{\text{ cm}}\) to represent \(5{\text{ cm}}\).[4]
e.Sam estimated the value of the mean of the measured lengths to be \(43{\text{ cm}}\).
Find the percentage error of Sam’s estimated mean.[2]
▶️Answer/Explanation
Markscheme
\(47.5{\text{ (cm)}}\) (A1)
(i) \(45.85{\text{ (cm)}}\) (G2)
Note: Accept \(45.9\) .
(ii) \(17.1{\text{ }}(17.0888 \ldots )\) (G1)
(iii) \(47.5{\text{ (cm)}}\) (G1)
\(62.5 – 32.5 = 30\) (M1)(A1)(G2)
Note: Award (M1) for correct quartiles seen.
(A1) for correct label and scale
(A1)(ft) for correct median
(A1)(ft) for correct quartiles and box
(A1) for endpoints at \(17.5\) and \(77.5\) joined to box by straight lines (A1)(A1)(ft)(A1)(ft)(A1)
Notes: The final (A1) is lost if the lines go through the box. Follow through from their parts (b) and (c).
\(\varepsilon = \left| {\frac{{43 – 45.85}}{{45.85}}} \right| \times 100\% \) (M1)
Note: Award (M1) for their correct substitution in \(\% \) error formula.
\( = 6.22\% \) (\(6.21592 \ldots \)) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b)(i). Accept \(6.32\% \) with use of \(45.9\) .
Question
The figure below shows the lengths in centimetres of fish found in the net of a small trawler.
a.Find the total number of fish in the net.[2]
b.Find (i) the modal length interval,
(ii) the interval containing the median length,
(iii) an estimate of the mean length.[5]
c.(i) Write down an estimate for the standard deviation of the lengths.
(ii) How many fish (if any) have length greater than three standard deviations above the mean?[3]
d.The fishing company must pay a fine if more than 10% of the catch have lengths less than 40cm.
Do a calculation to decide whether the company is fined.[2]
e.A sample of 15 of the fish was weighed. The weight, W was plotted against length, L as shown below.
Exactly two of the following statements about the plot could be correct. Identify the two correct statements.
Note: You do not need to enter data in a GDC or to calculate r exactly.
(i) The value of r, the correlation coefficient, is approximately 0.871.
(ii) There is an exact linear relation between W and L.
(iii) The line of regression of W on L has equation W = 0.012L + 0.008 .
(iv) There is negative correlation between the length and weight.
(v) The value of r, the correlation coefficient, is approximately 0.998.
(vi) The line of regression of W on L has equation W = 63.5L + 16.5.[2]
▶️Answer/Explanation
Markscheme
Total = 2 + 3 + 5 + 7 + 11 + 5 + 6 + 9 + 2 + 1 (M1)
(M1) is for a sum of frequencies.
= 51 (A1)(G2)[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) modal interval is 60 – 70
Award (A0) for 65 (A1)
(ii) median is length of fish no. 26, (M1)(A1)
also 60 – 70 (G2)
Can award (A1)(ft) or (G2)(ft) for 65 if (A0) was awarded for 65 in part (i).
(iii) mean is \(\frac{{2 \times 25 + 3 \times 35 + 5 \times 45 + 7 \times 55 + …}}{{51}}\) (M1)
(UP) = 69.5 cm (3sf) (A1)(ft)(G1)
Note: (M1) is for a sum of (frequencies multiplied by midpoint values) divided by candidate’s answer from part (a). Accept mid-points 25.5, 35.5 etc or 24.5, 34.5 etc, leading to answers 70.0 or 69.0 (3sf) respectively. Answers of 69.0, 69.5 or 70.0 (3sf) with no working can be awarded (G1).[5 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) (i) standard deviation is 21.8 cm (G1)
For any other answer without working, award (G0). If working is present then (G0)(AP) is possible.
(ii) \(69.5 + 3 \times 21.8 = 134.9 > 120\) (M1)
no fish (A1)(ft)(G1)
For ‘no fish’ without working, award (G1) regardless of answer to (c)(i). Follow through from (c)(i) only if method is shown.[3 marks]
5 fish are less than 40 cm in length, (M1)
Award (M1) for any of \(\frac{5}{51}\), \(\frac{46}{51}\), 0.098 or 9.8%, 0.902, 90.2% or 5.1 seen.
hence no fine. (A1)(ft)
Note: There is no G mark here and (M0)(A1) is never allowed. The follow-through is from answer in part (a).[2 marks]
(i) and (iii) are correct. (A1)(A1)[2 marks]
