Question
Consider the curve \(y = \sqrt{x}\).
(a) (i) Find \(\frac{dy}{dx}\).
(ii) Hence show that the equation of the tangent to the curve at the point (0.16, 0.4) is y = 1.25x + 0.2.
The shape of a piece of metal can be modelled by the region bounded by the functions f , g,
the x-axis and the line segment [AB], as shown in the following diagram. The units on the x
and y axes are measured in metres.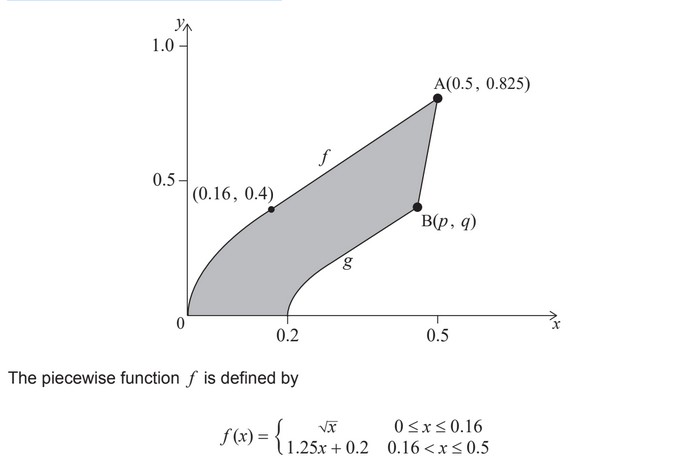
The graph of g is obtained from the graph of f by:
- a sketch scale factor of \(\frac{1}{2}\) in the x direction,
- followed by a stretch scale factor \(\frac{1}{2}\) in the y direction,
- followed by a translation of 0.2 units to the right.
Point A lies on the graph of f and has coordinates (0.5, 0.825). Point B is the image of A
under the given transformations and has coordinates (p , q).
(b) Find the value of p and the value of q.
The piecewise function g is given by
\(g(x)=\left\{\begin{matrix}
h(x) & 0.2 \leq x \leq a\\
1.25x + b & a<x \leq p
\end{matrix}\right.\)
(c) Find
(i) an expression for h(x).
(ii) the value of a.
(iii) the value of b.
(d) (i) Find the area enclosed by y = f (x), the x-axis and the line x = 0.5.
The area enclosed by y = g(x), the x-axis and the line x = p is 0.0627292 \(m^2\) correct to six significant figures.
(ii) Find the area of the shaded region on the diagram.
▶️Answer/Explanation
Ans:
(a) (i) \(y=x^{\frac{1}{2}}\)
\(\frac{dy}{dx}=\frac{1}{2} x^{-\frac{1}{2}}\)
(ii) gradient at x = 0.16 is \(\frac{1}{2} \times \frac{1}{\sqrt{0.16}}\)
= 1.25
EITHER
y – 0.4 = 1.25 (x – 0.16)
OR
0.4 = 1.25(0.16) + b
THEN
hence y = 1.25x + 0.2
(b) p q = = 0.45, 0.4125 ( 0.413) or (accept “(0.45, 0.4125)”)
(c) (i) \((h(x)=) \frac{1}{2} \sqrt{2(x-0.2)}\)
(ii) (a=) 0.28
(iii) EITHER
correct substitution of their part (b) (or (0.28, 0.2)) into the given expression
OR
\(\frac{1}{2}(1.25 \times 2 (x – 0.2)+0.2)\)
THEN
(b=) – 0.15
(d) (i) recognizing need to add two integrals
\(\int_{0}^{0.16} \sqrt{x}dx + \int_{0.16}^{0.5}(1.25x + 0.2)dx\)
0.251 \(m^2\) (0.250916…)
(ii) EITHER
area of trapezoid \(\frac{1}{2} \times 0.05(0.4125 + 0.825) = 0.0309375\)
OR
\(\int_{0.45}^{0.5}(8.25x – 3.3)dx = 0.0309375\)
THEN
shaded area = 0.250916… – 0.627292 – 0.0309375
= 0.157 \(m^2\) (0.15725)
Question
A particle moves in a straight line. The velocity, v ms–1 , of the particle at time t seconds is given by v (t) = t sint – 3 , for 0 ≤ t ≤ 10.
The following diagram shows the graph of v .
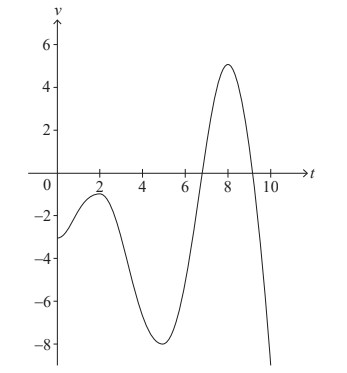
Find the smallest value of t for which the particle is at rest. [2]
Find the total distance travelled by the particle. [2]
Find the acceleration of the particle when t = 7 . [2]
▶️Answer/Explanation
Ans:
(a) recognising v=o t = 6.74416… = 6.74 (sec)
 = 37.0968… = 37.1 (m)
= 37.0968… = 37.1 (m)
(c) recognising acceleration at t = 7 is given by v’ (7) acceleration = 5.93430… = 5.93 (ms-2)
Question
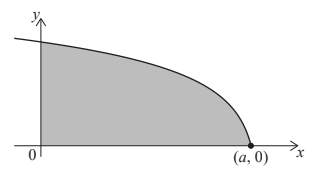
Let f (x) = \(\sqrt{12-2x}\) , x ≤ a . The following diagram shows part of the graph of f .
The shaded region is enclosed by the graph of f , the x-axis and the y-axis.
 x
x
The graph of f intersects the x-axis at the point (a , 0) .
Find the value of a . [2]
Find the volume of the solid formed when the shaded region is revolved 360° about the x-axis. [5]
▶️Answer/Explanation
Ans:
(a)
recognize f (x) = 0
eg \(\sqrt{12-2x}= 0, 2x=12\)
a= 6 (accept x= 6, (6,0))
(b)
attempt to substitute either their limits or the function into volume formula (must involve \(f^{2})\)
eg \(\int_{0}^{6}f^{2}dx , \pi \int (\sqrt{12-2x})^{2}, \pi \int_{0}^{6}\)(12-2x) dx
correct integaration of each term
eg \(12x-x^{2}, 12x-x^{2}\)+c, \(\left [ 12x-x^{2} \right ]_0^6\)
substituting limits into their integrated function and subtracting (in any order)
eg \(\pi (12(6)-(6)^{2})-\pi (0),72\pi -36\pi ,(12(6)-(6)^{2})-(0)\)
volume = \(36\pi \)
Question
a.Find \(\int {\frac{1}{{2x + 3}}} {\rm{d}}x\) .[2]
b.Given that \(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \ln \sqrt P \) , find the value of P.[4]
▶️Answer/Explanation
Markscheme
\(\int {\frac{1}{{2x + 3}}} {\rm{d}}x = \frac{1}{2}\ln (2x + 3) + C\) (accept \(\frac{1}{2}\ln |(2x + 3)| + C\) ) A1A1 N2
[2 marks]
\(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \left[ {\frac{1}{2}\ln (2x + 3)} \right]_0^3\)
evidence of substitution of limits (M1)
e.g.\(\frac{1}{2}\ln 9 – \frac{1}{2}\ln 3\)
evidence of correctly using \(\ln a – \ln b = \ln \frac{a}{b}\) (seen anywhere) (A1)
e.g. \(\frac{1}{2}\ln 3\)
evidence of correctly using \(a\ln b = \ln {b^a}\) (seen anywhere) (A1)
e.g. \(\ln \sqrt {\frac{9}{3}} \)
\(P = 3\) (accept \(\ln \sqrt 3 \) ) A1 N2
[4 marks]
Question
Let \(\int_1^5 {3f(x){\rm{d}}x = 12} \) .
a.Show that \(\int_5^1 {f(x){\rm{d}}x = – 4} \) .[2]
b.Find the value of \(\int_1^2 {(x + f(x)){\rm{d}}x + } \int_2^5 {(x + f(x)){\rm{d}}x} \) .[5]
▶️Answer/Explanation
Markscheme
evidence of factorising 3/division by 3 A1
e.g. \(\int_1^5 {3f(x){\rm{d}}x = 3\int_1^5 {f(x){\rm{d}}x} } \) , \(\frac{{12}}{3}\) , \(\int_1^5 {\frac{{3f(x){\rm{d}}x}}{3}} \) (do not accept 4 as this is show that)
evidence of stating that reversing the limits changes the sign A1
e.g. \(\int_5^1 {f(x){\rm{d}}x = } – \int_1^5 {f(x){\rm{d}}x} \)
\(\int_5^1 {f(x){\rm{d}}x = } – 4\) AG N0
[2 marks]
evidence of correctly combining the integrals (seen anywhere) (A1)
e.g. \(I = \int_1^2 {(x + f(x)){\rm{d}}x + } \int_2^5 {(x + f(x)){\rm{d}}x = } \int_1^5 {(x + f(x)){\rm{d}}x} \)
evidence of correctly splitting the integrals (seen anywhere) (A1)
e.g. \(I = \int_1^5 {x{\rm{d}}x + } \int_1^5 {f(x){\rm{d}}x} \)
\(\int {x{\rm{d}}x = } \frac{{{x^2}}}{2}\) (seen anywhere) A1
\(\int_1^5 {x{\rm{d}}x = } \left[ {\frac{{{x^2}}}{2}} \right]_1^5 = \frac{{25}}{2} – \frac{1}{2}\) \(\left( { = \frac{{24}}{2},12} \right)\) A1
\(I =16\) A1 N3
[5 marks]