Question
The nth term of an arithmetic sequence is given by un = 15 – 3n.
(a) State the value of the first term, u1 .
(b) Given that the nth term of this sequence is -33, find the value of n.
(c) Find the common difference, d.
Answer/Explanation
Ans:
(a) u1 =12
(b) 15 – 3n = -33
n = 16
(c) valid approach to find d
u2 – u1 = 9 – 12 OR recognize gradient is −3 OR attempts to solve
-33 = 12 + 15 d
d = -3
Question
The continuous random variable X has probability density function
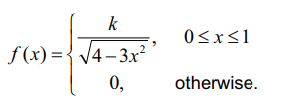
(a) Find the value of k .
(b) Find E(X) .
Answer/Explanation
Ans:
(a) attempt to integrate \(\frac{k}{\sqrt{4-3x^{2}}}\)
\(= k \left \lfloor \frac{1}{\sqrt{3}}arcsin\left ( \frac{\sqrt{3}}{2}x \right ) \right \rfloor\)
Note: Award (M1)A0 for arcsin \(\left ( \frac{\sqrt{3}}{2}x \right )\)
Condone absence of k up to this stage.
equating their integrand to 1
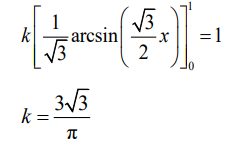
(b) \(E(X) = \frac{3\sqrt{3}}{\pi }\int_{0}^{1}\frac{x}{\sqrt{4-3x^{2}}}dx\)
Note: Condone absence of limits if seen at a later stage.
EITHER
attempt to integrate by inspection
\( = \frac{3\sqrt{3}}{\pi }\times -\frac{1}{6}\int -6x\left ( 4-3x^{2} \right )^{-\frac{1}{2}}dx\)
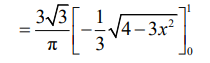
Note: Condone the use of k up to this stage.
OR
for example, \(u = 4-3c^{2} \Rightarrow \frac{du}{dx}= -6x\)
Note: Other substitutions may be used. For example, u = −3x2.
\(= – \frac{\sqrt{3}}{2\pi } \int_{4}^{1}u^{-\frac{1}{2}} du\)
Note: Condone absence of limits up to this stage.

