Question
[Maximum mark: 6]
Two events $A$ and $B$ are such that $\mathrm{P}(A \cup B)=0.78, \mathrm{P}(A \cap B)=0.27$ and $\mathrm{P}(A \mid B)=0.45$
(a) Find $\mathrm{P}(B)$ [2]
(b) Find $\mathrm{P}(A)$. [2]
(c) Hence show that events $A^{\prime}$ and $B$ are independent. [2]
Answer/Explanation
(a) Using the conditional probability formula, we get
$
\begin{aligned}
\mathrm{P}(A \mid B) & =\frac{\mathrm{P}(A \cap B)}{\mathrm{P}(B)} \\
0.45 & =\frac{0.27}{\mathrm{P}(B)} \\
\mathrm{P}(B) & =0.6\quad \text { [by using G.D.C.] }
\end{aligned}
$
(b) Using the combined events formula, we obtain
$
\begin{aligned}
\mathrm{P}(A \cup B) & =\mathrm{P}(A)+\mathrm{P}(B)-\mathrm{P}(A \cap B) \\
0.78 & =\mathrm{P}(A)+0.6-0.27 \\
\mathrm{P}(A) & =0.45 \quad \text { [by using G.D.C.] }
\end{aligned}
$
(c) Using the equality $A^{\prime} \cap B=B \backslash(A \cap B)$, we have
$
\begin{aligned}
\mathrm{P}\left(A^{\prime} \cap B\right) & =\mathrm{P}(B)-\mathrm{P}(A \cap B) \\
& =0.6-0.27 \\
& =0.33
\end{aligned}
$
Using the complementary events formula, we have
$
\begin{aligned}
\mathrm{P}\left(A^{\prime}\right) \mathrm{P}(B) & =[1-\mathrm{P}(A)] \mathrm{P}(B) \\
& =[1-0.45](0.6) \\
& =0.33
\end{aligned}
$
Since $\mathrm{P}\left(A^{\prime} \cap B\right)=0.33=\mathrm{P}\left(A^{\prime}\right) \mathrm{P}(B)$, events $A^{\prime}$ and $B$ are independent.
Question
[Maximum mark: 5]
Let $f(x)=9-2 \ln \left(x^2+4\right)$, for $x \in \mathbb{R}$. The graph of $f$ passes through the point $(p, 3)$, where $p>0$.
(a) Find the value of $p$.
The following diagram shows part of the graph of $f$. [2]
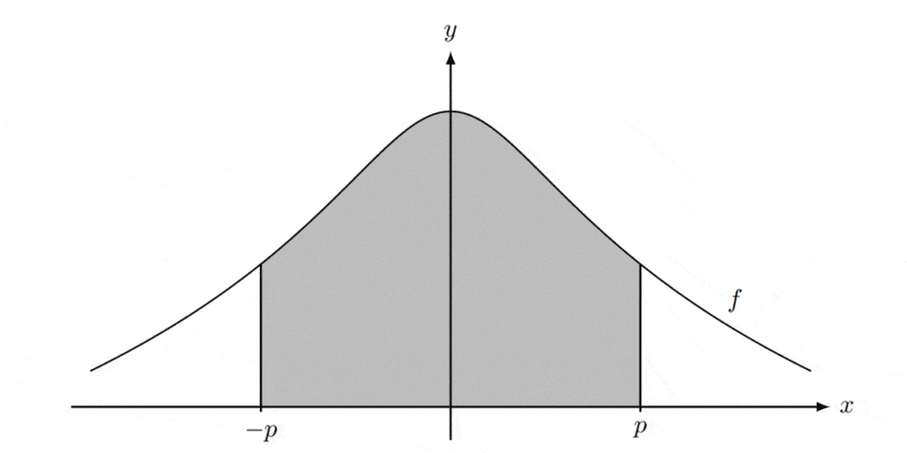
The region enclosed by the graph of $f$, the $x$-axis and the lines $x=-p$ and $x=p$ is rotated $360^{\circ}$ about the $x$-axis.
(b) Find the volume of the solid formed. [3]
Answer/Explanation
(a) We have
$
\begin{aligned}
f(p) & =3 \\
9-2 \ln \left(p^2+4\right) & =3 \\
p & =4.01\quad \text { [by using G.D.C.] }
\end{aligned}
$
(b) The volume of revolution is
$
\begin{gathered}
V=\pi \int_{-4.01}^{4.01}\left(9-2 \ln \left(x^2+4\right)\right)^2 \mathrm{~d} x \\
=605 \quad \text { [by using G.D.C.] }
\end{gathered}
$
