Question
Consider the curve with equation y = (2x – 1)ekx , where x ∈ R and k ∈ Q.
The tangent to the curve at the point where x = 1 is parallel to the line y = 5ekx .
Find the value of k .
Answer/Explanation
Ans: evidence of using product rule
\(\frac{dy}{dx}=(2x-1)\times (ke^{kx})+2\times e^{kx}(=e^{kx}(2kx-k+2))\)
correct working for one of (seen anywhere)
\(\frac{dy}{dx}at x = 1 \Rightarrow ke^{k}+2e^{k}\)
OR
slope of tangent is 5ek
their \(\frac{dy}{dx}\) at x =1 equals the slope of y = 5ekx (= 5ek) (seen anywhere)
kek + 2ek = 5ek
k = 3
Question
Let f(x) = 3x2 – 4x. The graph of f is shown in the following diagram.
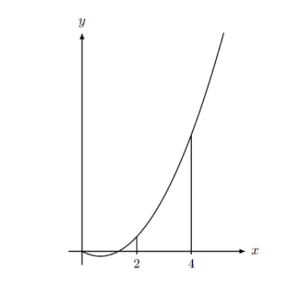
(a) Find ∫ (3x2 – 4x) dx.
(b) Find the area of the region enclosed by the graph of f, the x-axis and the lines x = 2 and x = 4.
Answer/Explanation
Ans:
(a) ∫ (3x2 – 4x) dx = ∫ 3x2 dx + ∫ ( – 4x) dx
\(=\frac{3x^{3}}{3}-\frac{4x^{2}}{2}+C\)
= x3 – 2x2 + C
(a) The area enclosed by the graph of f, the x-axis and the lines x = 2 and x = 4 is given by
\(A = \int_{2}^{4}(3x^{2}-4x)dx\)
\(= (x^{3}-2x^{2})|_{2}^{4}\)
= [43 – 2(42)] – [23 – 2(22)]
= [64 – 32 ] – [ 8 – 8]
= 32
