Question
The derivative of a function g is given by g ′(x) = 3x2 + 5ex, where x ∈ R. The graph of g passes through the point (0, 4). Find g(x).
Answer/Explanation
Ans:
METHOD 1
recognises that \(g(x)= \int \left ( 3x^{2} +5e^{x}\right )dx\)
\(g(x)= x^{3}+5e^{x}(+C)\)
Note: Award A1 for each integrated term.
substitutes x = 0 and y = 4 into their integrated function (must involve +C)
4 = 0 + 5 + C ⇒ C = -1
\(g(x)= x^{3}+5e^{x}-1\)
METHOD 2
attempts to write both sides in the form of a definite integral
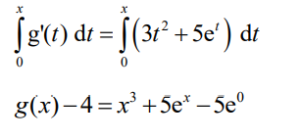
Note: Award A1 for g x( ) 4 − and A1 for \(x^{3}+5e^{x}-5e^{0}.
\(g(x)= x^{3}+5e^{x}-1\)
Question
In an arithmetic sequence, $\mathrm{u}_6=24, \mathrm{u}_{13}=80$.
(a) Find the common difference.
(b) Find the first term.
(c) Find the sum of the first 30 terms in the sequence.
Answer/Explanation
Ans:
(a) To find the common difference, we can use the formula for the $n$th term of an arithmetic sequence: $\mathrm{u}_n=\mathrm{u}_1+(n-1)d$, where $d$ is the common difference.
Using this formula, we can write:
\begin{align*}
\mathrm{u}_6 &= \mathrm{u}_1 + 5d = 24 \\
\mathrm{u}_{13} &= \mathrm{u}_1 + 12d = 80
\end{align*}
We can solve this system of equations for $d$ by subtracting the first equation from the second equation:
\begin{align*}
\mathrm{u}_{13} – \mathrm{u}_6 &= (\mathrm{u}_1 + 12d) – (\mathrm{u}_1 + 5d) \\
&= 7d \\
&= 80 – 24 \\
&= 56
\end{align*}
Therefore, the common difference is $d=56/7=8$.
(b) To find the first term, we can use the formula for the $n$th term of an arithmetic sequence again. Using the value of the common difference that we found in part (a), we have:
\begin{align*}
\mathrm{u}_6 &= \mathrm{u}_1 + 5d \\
24 &= \mathrm{u}_1 + 5(8) \\
24 &= \mathrm{u}_1 + 40 \\
\mathrm{u}_1 &= -16
\end{align*}
Therefore, the first term is $\mathrm{u}_1=-16$.
(c) To find the sum of the first 30 terms, we can use the formula for the sum of the first $n$ terms of an arithmetic sequence:
\begin{align*}
\mathrm{S}_n &= \frac{n}{2}(\mathrm{u}_1 + \mathrm{u}_n) \\
&= \frac{n}{2}(\mathrm{u}_1 + (\mathrm{u}_1 + (n-1)d)) \\
&= \frac{n}{2}(2\mathrm{u}_1 + (n-1)d)
\end{align*}
Using the values we found in parts (a) and (b), we have:
\begin{align*}
\mathrm{S}_{30} &= \frac{30}{2}(2(-16) + (30-1)(8)) \\
&= 15(-32 + 232) \\
&= 3000
\end{align*}
Therefore, the sum of the first 30 terms is $\mathrm{S}_{30}=3000$.
