Question
The following diagram shows a circle with centre O and radius 10 cm.
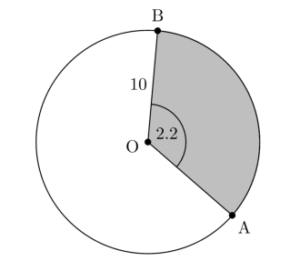
Points A, B lie on the circle and \(A\hat{O}B\) = 2.2 radians.
(a) Find:
(i) the length of the minor arc AB;
(ii) the perimeter of the shaded region.
(b) Find the area of the shaded region.
Answer/Explanation
Ans:
(a) (i) Using the length of an arc formula, we get
\(l_{arc}=(A\hat{O}B)(OA)\)
= (2.2)(10)
= 22 cm
(ii) Hence the perimeter of the shaded region is
\(P_{region}=2(OA)+l_{arc}\)
= 2(10) + 22
= 42 cm
(b) Using the area of a sector formula, we obtain
\(A_{region}=\frac{1}{2}[OA^{2}](A\hat{O}B)\)
\(=\frac{1}{2}[10^{2}](2.2)\)
=110 cm2
Question
Consider a function f(x) such that \(\int_{1}^{5}f(x)dx=6.\)
(a) Find \(\int_{1}^{5}2f(x)dx.\)
(b) Find \(\int_{1}^{5}(f(x)+3)dx.\)
Answer/Explanation
Ans:
(a) \(\int_{1}^{5}2f(x)dx=2\int_{1}^{5}f(x)dx\)
= 2(6)
= 12
(b) \(\int_{1}^{5}(f(x)+3)dx=\int_{1}^{5}f(x)dx+\int_{1}^{5}3dx\)
\(=6+[3x]|_{1}^{5}\)
= 6 + [15 – 3]
= 18
