Question
An arithmetic sequence is given by 3, 5, 7, …..
(a) Write down the value of the common difference, d.
(b) Find
(i) u10;
(ii) S10.
(c) Given that un = 253, find the value of n.
Answer/Explanation
Ans:
(a) We have u1 = 3 and u2 = 5.
Hence the value of d is
d = u2 – u1
= 5 – 3
= 2
(b) (i) Using the nth term formula un = u1 + (n – 1)d with n = 10, we get
u10 = u1 + (10 – 1)d
= 3 + (10 – 1) (2)
= 21
(ii) Using the sum of n terms formula \(S_{n}=\frac{n}{2}(u_{1}+u_{n})\) with n = 10, we find
\(S_{10}=\frac{10}{2}(u_{1}+u_{10})\)
\(=\frac{10}{2}(3+21)\)
= 120
(c) Substituting un = 253, u1 = 3 and d = 2 in un = u1 + (n – 1)d and solving the resulting equation for n, we obtain
253 = 3 + (n – 1) (2)
253 = 2n + 1
252 = 2n
n = 126
Question
The following Venn diagram shows two events A and B, where P(A) = 0.3, P(B) = 0.8 and P(A ∩ B) = 0.2. The values of p, q, r and s are probabilities.
(a) Find the value of r, p, q and s.
(b) Find P(A | B’).
Answer/Explanation
Ans:
(a) We have
r = 0.2
Using the Venn diagram, we get
P(A) = p + P(A ∩ B)
0.3 = p + 0.2
p = 0.1
Using the Venn diagram, we get
P(B) = P(A ∩ B) + q
0.8 = 0.2 + q
q = 0.6
P(U) = P(A ∪ B) + s
1 = (p + r + q) + s
1 = (0.1 + 0.2 + 0.6) + s
s = 0.1
(b) If we shade in the region that represents A ∩ B’ , we have
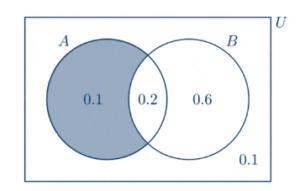
Hence, using the conditional probability formula, we find
\(P(A|B’)=\frac{P(A\cap B’)}{P(B’)}=\frac{01}{0.2}\)
\(=\frac{1}{2}\)
