Question
The cross-section of a beach is modelled by the equation \(y = 0.02x^2\) for \(0 \leq x \leq 10\) where y is the height of the beach (in metres) at a horizontal distance x metres form an origin.
t is the time in hours after low tide.
At t=0 the water is at point (0,0). The height of the water rises at a rate of 0.2 metres per hour. The point W(x(t), y(t)) indicates where the water level meets the beach at time t.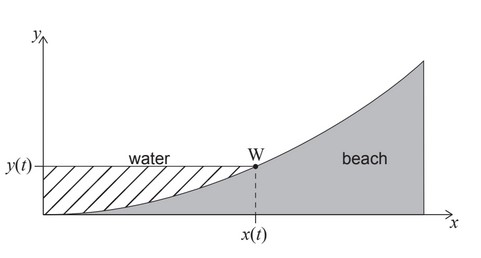
(a) When W has an x-coordinate equal to 1, find the horizontal component of the velocity
of W.
A snail is modelled as a single point. At t = 0 it is positioned at (1 , 0.02). The snail travels
away from the incoming water at a speed of 1 metre per hour in the direction along the curve
of the cross-section of the beach. The following diagram shows this for a value of t, such
that t > 0.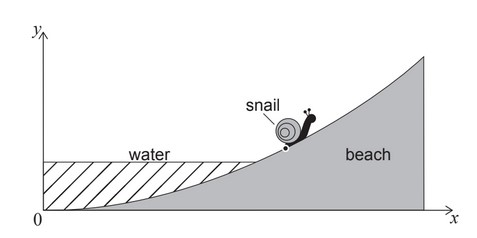
(b) (i) Find the time taken for the snail to reach the point (10 , 2).
(ii) Hence show that the snail reaches the point (10 , 2) before the water does.
Answer/Explanation
Ans:
(a) use of chain rule
\(\frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt}\)
attempt to find \(\frac{dy}{dx}\) at x = 1
\(0.2 = 0.04 \times \frac{dx}{dt}\)
\((\frac{dx}{dt}=)\) = 5 \(mh^{-1}\)
(b) (i) if the position of the snail is (X, Y)
from part (a) \(\frac{dX}{dt} = \frac{1}{0.04X}\frac{dY}{dt}\)
since speed is 1:
finding modulus of velocity vector and equating to 1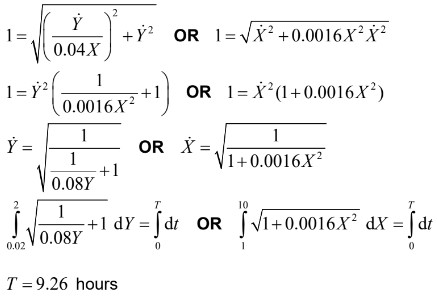
(ii) EITHER
time for water to reach top is \(\frac{0}{0.2}=10\) hours (seen anywhere)
OR
or at time t = 9.26, height of water is \(0.2 \times 9.26 = 1.852\)
THEN
so the water will not reach the snail
Question
Consider the following directed network.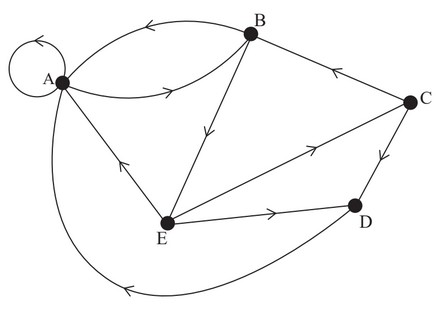
(a) Write down the adjacency matrix for this network.
(b) Determine the number of different walks of length 5 that start and end at the same vertex.
Answer/Explanation
Ans:
(a) 
(b) raising their matrix to a power of 5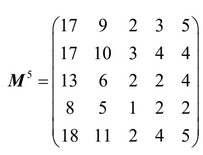
(the required number is 17 10 2 2 5 ) + +++= 36
