Question
The following Argand diagram shows a circle centre 0 with a radius of 4 units.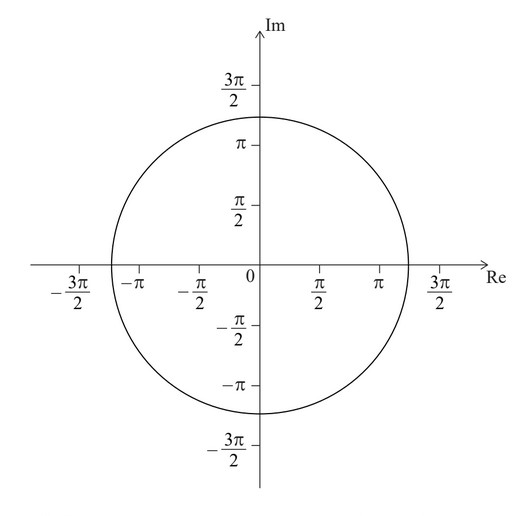
A set of points, \({z_{\theta}}\), on the Argand plane are defined by the equation
\(z_{\theta} =\frac{1}{2} \theta e^{\theta i}\), where \(\theta \geq 0\).
(a) Plot on the Argand diagram the points corresponding to
(i) \(\theta = \frac{\pi}{2}\).
(ii) \(\theta = \pi\)
(ii) \(\theta = \frac{3 \pi}{2}\)
Consider the case where \(|z_{\theta} |=4\).
(b) (i) Find the value of \(\theta\).
(ii) For this value of \(\theta\), plot the approximate position of \(z_{\theta}\) on the Argand diagram.
Answer/Explanation
Ans:
(a)
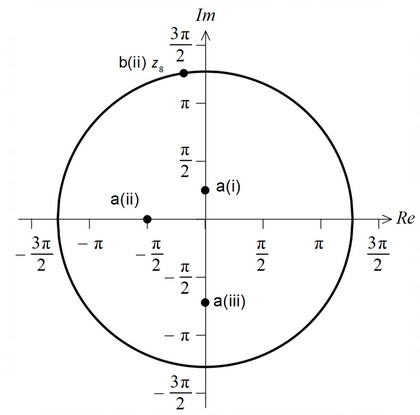
(b) (i) \(\frac{1}{2} \theta = 4\)
\(\Rightarrow \theta = 8\)
(ii) \(z_8\) is shown in the diagram above
Question
A solid right circular cone has a base radius of $18 \mathrm{~cm}$ and a slant height of $30 \mathrm{~cm}$. A smaller right circular cone, with a vertical height of $8 \mathrm{~cm}$ and a slant height of $10 \mathrm{~cm}$, is removed from the top of the larger cone, as shown in the diagram.
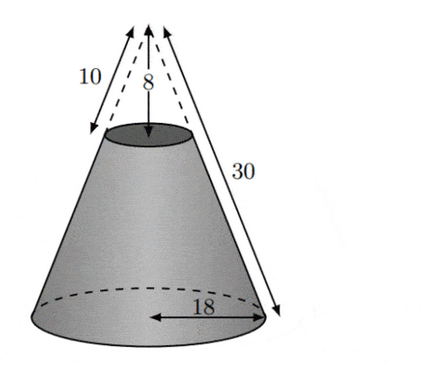
(a) Calculate the radius of the base of the cone which has been removed. [2]
(b) Calculate the curved surface area of the cone which has been removed. [2]
(c) Calculate the curved surface area of the remaining solid. [2]
Answer/Explanation
(a) Consider the following right-angled triangle:
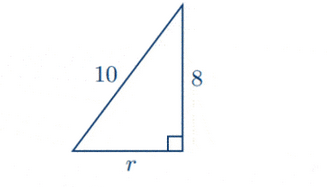
Using Pythagorean formula, we get
$
\begin{aligned}
10^2 & =8^2+r^2 \\
r^2 & =10^2-8^2 \\
r & =\sqrt{100-64} \\
& =6 \mathrm{~cm}
\end{aligned}
$
(b) Utilizing the surface area formula for a cone, we get
$
\begin{aligned}
A & =\pi r L \\
A & =\pi(6)(10) \\
& \approx 188 \mathrm{~cm}^2
\end{aligned}
$
(c) The curved surface area of the remaining solid is the curved surface area of the initial cone subtracting the curved surface area of the removed cone.
Let’s find the curved surface area of the initial cone.
$
\begin{aligned}
A & =\pi r L \\
A & =\pi(18)(30) \\
& \approx 1696 \mathrm{~cm}^2 .
\end{aligned}
$
Hence
$
\begin{aligned}
A_{\text {remaining }} & =1696-188 \\
& =1508 \\
& \approx 1510 \mathrm{~cm}^2
\end{aligned}
$
