Question
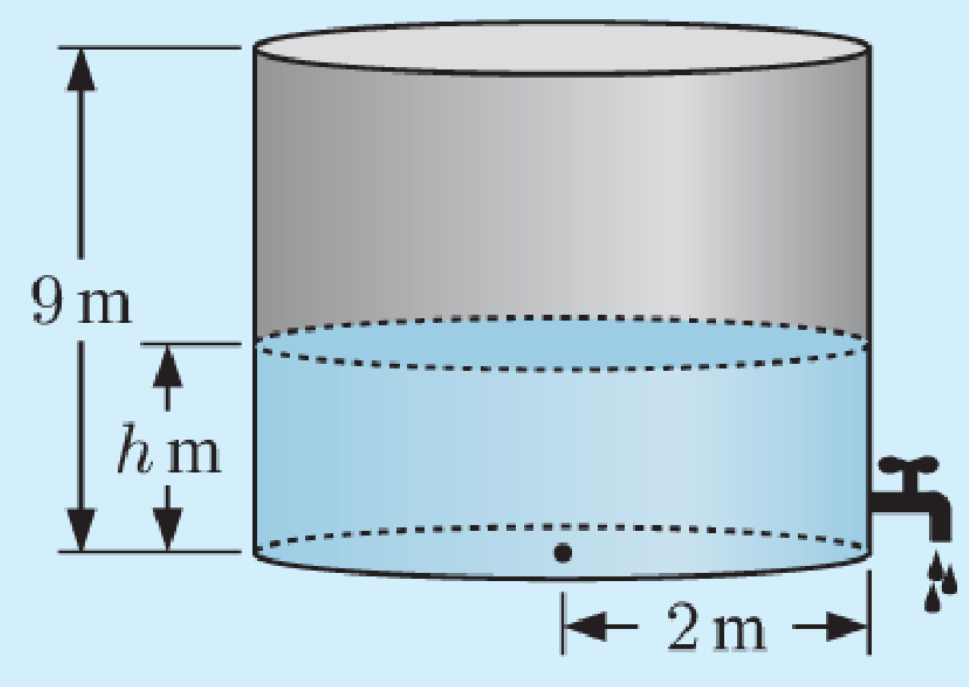
Water flows out of a tap at the bottom of a large cylindrical tank with base radius $2 \mathrm{~m}$. The rate at which the water flows is proportional to the square root of the depth of the water remaining in the tank. Initially the tank is full to a depth of $9 \mathrm{~m}$. After 15 minutes the water is $4 \mathrm{~m}$ deep. How long will it take for the tank to empty?
▶️Answer/Explanation
Solution:
We are given that $\frac{d V}{d t} \propto \sqrt{h}$ where $h$ is the depth of the water.
$\therefore \quad \frac{d V}{d t}=k \sqrt{h} \quad$ where $k$ is a constant.
$$
\begin{aligned}
\therefore \quad \frac{d V}{d h} \frac{d h}{d t} & =k \sqrt{h} \quad\{\text { chain rule }\} \\
\therefore 4 \pi \frac{d h}{d t} & =k \sqrt{h} \quad\left\{V=\pi r^2 h=4 \pi h \quad \therefore \quad \frac{d V}{d h}=4 \pi\right\} \\
\therefore \quad \frac{4 \pi}{\sqrt{h}} \frac{d h}{d t} & =k \\
\therefore \quad \int 4 \pi h^{-\frac{1}{2}} \frac{d h}{d t} d t & =\int k d t \\
\therefore 4 \pi \int h^{-\frac{1}{2}} d h & =\int k d t \\
\therefore 4 \pi \frac{h^{\frac{1}{2}}}{\frac{1}{2}} & =k t+c \\
\therefore 8 \pi \sqrt{h} & =k t+c
\end{aligned}
$$
Now when $t=0, h=9$, so $8 \pi \sqrt{9}=c$
$$
\begin{aligned}
\therefore c & =24 \pi \\
\therefore \quad 8 \pi \sqrt{h} & =k t+24 \pi
\end{aligned}
$$
Also, when $t=15, h=4$, so $8 \pi \sqrt{4}=15 k+24 \pi$
$$
\begin{aligned}
\therefore \quad 15 k & =-8 \pi \\
\therefore \quad k & =-\frac{8 \pi}{15}
\end{aligned}
$$
So, the equation connecting the depth of the water and the time $t$ is $8 \pi \sqrt{h}=-\frac{8 \pi}{15} t+24 \pi$. The tank is empty when $h=0$. This occurs when $\frac{8 \pi}{15} t=24 \pi$
$$
\therefore t=45
$$
The tank empties in 45 minutes.
Question
The system $\left\{\begin{array}{l}\frac{d x}{d t}=-8 x-5 y \\ \frac{d y}{d t}=10 x+7 y\end{array} \quad\right.$ can be written in the matrix form $\dot{\mathbf{x}}=\mathbf{A x}$ where
$\mathbf{A}=\left(\begin{array}{cc}-8 & -5 \\ 10 & 7\end{array}\right)$ has eigenvalues $2,-3$ with corresponding eigenvectors $\left(\begin{array}{c}1 \\ -2\end{array}\right),\left(\begin{array}{c}-1 \\ 1\end{array}\right)$ respectively.
a. Given the initial point $(1,2)$, find:
i) $\dot{\mathbf{x}}$ when $t=0$
ii) the particular solution to the system.
b. Sketch the phase portrait, including the particular solution.
c. Discuss the behaviour of the system in the long term.
▶️Answer/Explanation
Sol:
a (i).
When $t=0, \quad\left(\begin{array}{l}x \\ y\end{array}\right)=\left(\begin{array}{l}1 \\ 2\end{array}\right)$
$$
\therefore \quad \dot{\mathbf{x}}=\left(\begin{array}{cc}
-8 & -5 \\
10 & 7
\end{array}\right)\left(\begin{array}{l}
1 \\
2
\end{array}\right)=\left(\begin{array}{c}
-18 \\
24
\end{array}\right)
$$
a (ii).
Using the given eigenvalues and eigenvectors, a general solution to the system is
$$
\mathbf{x}=A e^{2 t}\left(\begin{array}{c}
1 \\
-2
\end{array}\right)+B e^{-3 t}\left(\begin{array}{c}
-1 \\
1
\end{array}\right)
$$
When $t=0$, we know $\mathbf{x}=\left(\begin{array}{l}1 \\ 2\end{array}\right)$
$$
\begin{aligned}
\therefore \quad A\left(\begin{array}{c}
1 \\
-2
\end{array}\right)+B\left(\begin{array}{c}
-1 \\
1
\end{array}\right) & =\left(\begin{array}{l}
1 \\
2
\end{array}\right) \\
\therefore \quad\left(\begin{array}{cc}
1 & -1 \\
-2 & 1
\end{array}\right)\left(\begin{array}{l}
A \\
B
\end{array}\right) & =\left(\begin{array}{l}
1 \\
2
\end{array}\right) \\
\therefore\left(\begin{array}{l}
A \\
B
\end{array}\right) & =\left(\begin{array}{cc}
1 & -1 \\
-2 & 1
\end{array}\right)^{-1}\left(\begin{array}{l}
1 \\
2
\end{array}\right) \\
\therefore\left(\begin{array}{l}
A \\
B
\end{array}\right) & =\left(\begin{array}{l}
-3 \\
-4
\end{array}\right)
\end{aligned}
$$
The particular solution is $\mathbf{x}=-3 e^{2 t}\left(\begin{array}{c}1 \\ -2\end{array}\right)-4 e^{-3 t}\left(\begin{array}{c}-1 \\ 1\end{array}\right)$.
b) The equilibrium point at $\mathrm{O}$ is a saddle point.
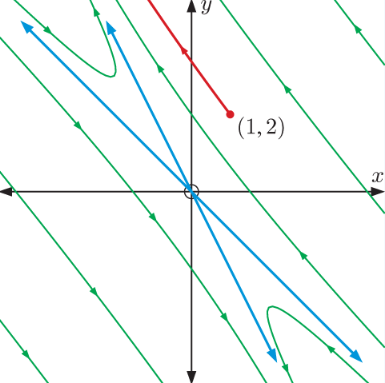
c)
As $t \rightarrow \infty, \quad e^{-3 t} \rightarrow 0$
$$
\therefore \quad \mathbf{x} \rightarrow-3 e^{2 t}\left(\begin{array}{c}
1 \\
-2
\end{array}\right)
$$
$\therefore$ the line $k\left(\begin{array}{c}1 \\ -2\end{array}\right)$ will be an asymptote as $t \rightarrow \infty$.
