Question
[Maximum mark: 17]
The following table shows the average height, $x$, and the average trunk diameter, $y$, of eight species of tree.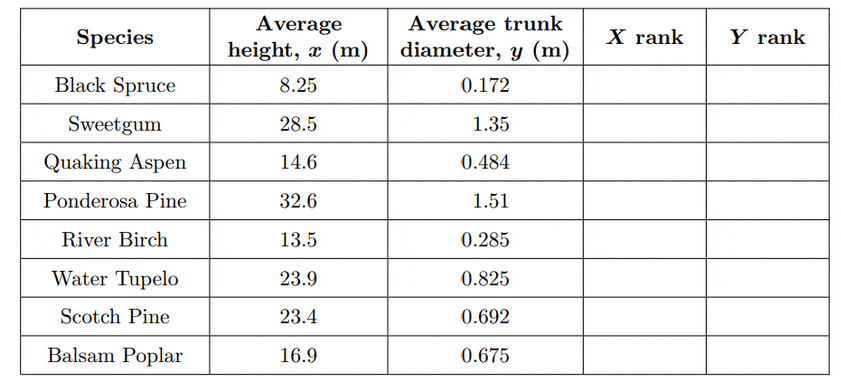
(a) Find the range of the average heights for these eight species of tree, correct to two decimal places. [2]
(b) From the data from of these eight species of tree
(i) calculate the Pearson’s product-moment correlation coefficient, $r$;
(ii) describe the correlation between the average height and the average trunk diameter. [4]
(c) Write down the line of regression equation, $y$ on $x$, in the form $y=m x+c$. [2]
The average height of another tree species, Black Ash, is $15.2 \mathrm{~m}$.
(d) Use your regression line to estimate the average trunk diameter of Black Ash. [2]
The average diameter of Black Ash is found to be $0.445 \mathrm{~m}$.
(e) Find the percentage error in your estimate in part (d). [2]
The average height of another tree species, Alpine Ash, is $87.5 \mathrm{~m}$.
(f) State whether it is valid to use the regression line to estimate the average trunk diameter of Alpine Ash. Give a reason for your answer. [2]
(g) Complete the two empty rank columns in the table and state why the Spearman’s rank correlation coefficient could be calculated by inspection. [4]
Answer/Explanation
(a) The range of the average heights for these eight species of tree is
$
\begin{aligned}
\text { [range of } x] & =\operatorname{Max}-\text { Min } \\
& =32.6-8.25 \\
& 24.35
\end{aligned}
$
(b) (i) $r \approx 0.959$ $\text{[by using G.D.C.]}$
(ii) Since the correlation coefficient is positive and close to 1 , there is a very strong positive correlation between the average height and the average trunk diameter.
(c) $y=0.0551 x-0.364$ $\text{[by using G.D.C.]}$
(d) Substituting $x=15.2$ into the equation of the regression line, we get
$
\begin{gathered}
y=0.0551(15.2)-0.364 \\
\approx 0.474 \mathrm{~m}
\end{gathered}
$
Question
[Maximum mark: 8]
The bench press world record weight, $W$, in kilograms, is modelled by the function
$$
W(t)=\frac{M}{1+C e^{-0.04 t}},
$$
where $t$ is the number of years that have passed since 1953 .
The first bench press world record of $227.27 \mathrm{~kg}$ was set in 1953. According to bench press experts, the record weight will eventually reach a limit of $350 \mathrm{~kg}$.
(a) (i) Write down the value of $M$.
(ii) Find the value of $C$, giving your answer correct to 2 decimal places. [3]
(b) The current unbeaten bench press world record weight is $337 \mathrm{~kg}$. Find the year in which this record was set. [2]
(c) A young and promising powerlifter claims that he is going to break any bench press world record performed until 2025. Find the weight that he has to bench press in 2025 to set a new bench press world record according to the model. [3]
Answer/Explanation
(a) (i) $M=350$
(ii) Solving the equation $W(0)=227.27$ for $C$, we get
$
\begin{aligned}
\frac{350}{1+C e^{-0.04(0)}} & =227.27 \\
\frac{350}{1+C} & =227.27 \\
C & \approx 0.54\quad\text{[by using G.D.C.]}
\end{aligned}
$
(b) Solving the equation $W(t)=337$ for $t$, we obtain
$
\begin{aligned}
\frac{350}{1+0.54 e^{-0.04 t}} & =337 \\
t & \approx 66\quad\text{[by using G.D.C.]}
\end{aligned}
$
Hence we have
$
\begin{array}{|c|c|c|c|}
\hline t & 0 & 1 & 66 \\
\hline \text { Year } & 1953 & 1954 & 2019 \\
\hline
\end{array}
$
Hence the current unbeaten bench press world record was set in 2019
(c) We have
$
\begin{array}{|c|c|c|c|}
\hline \text { Year } & 1953 & 2019 & 2025 \\
\hline t & 0 & 66 & 72 \\
\hline
\end{array}
$
Hence, evaluating $W(t)$ for $t=72$, we find
$
\begin{aligned}
W(72) & =\frac{350}{1+0.54 e^{-0.04(72)}} \\
& \approx 340 \mathrm{~kg}
\end{aligned}
$
