Question
[Maximum mark: 6]
Let $F=\frac{(4 \sin 2 z-1)(2 \tan 3 z+1)}{x^2-y^2}$, where $x=12, y=8$ and $z=15^{\circ}$.
(a) Calculate the exact value of $F$. [2]
(b) Give your answer to $F$ correct to
(i) two significant figures;
(ii) two decimal places. [2]
Sasha estimates the value of $F$ to be $0.03$.
(c) Calculate the percentage error in Sasha’s estimate. [2]
Answer/Explanation
(a) Substituting $x=12, y=8$ and $z=15^{\circ}$ in the expression for $F$, we get
$
\begin{aligned}
F & =\frac{\left(4 \sin 30^{\circ}-1\right)\left(2 \tan 45^{\circ}+1\right)}{12^2-8^2} \\
& =0.0375
\end{aligned}
$
(b) (i) $0.038$
(ii) $0.04$
(c) Using the percentage error formula $\epsilon=\left|\frac{v_{\mathrm{A}}-v_{\mathrm{E}}}{v_{\mathrm{E}}}\right| \times 100 \%$ with $v_{\mathrm{E}}=0.0375$ and $v_{\mathrm{A}}=0.03$, we obtain
$
\begin{aligned}
\epsilon & =\left|\frac{0.03-0.0375}{0.0375}\right| \times 100 \% \\
& =20 \%
\end{aligned}
$
Question
[Maximum mark: 6]
The probability that Amanda successfully passes her maths exam depends on the exam topic. The probability that the topic is statistics is $0.35$ and the probability she passes this topic is only $0.3$. The probability that Amanda passes any other topic during the exam is $0.8$.
(a) Complete the following tree diagram. [3]

(b) Find the probability that Amanda does not pass the exam. [3]
Answer/Explanation
(a)
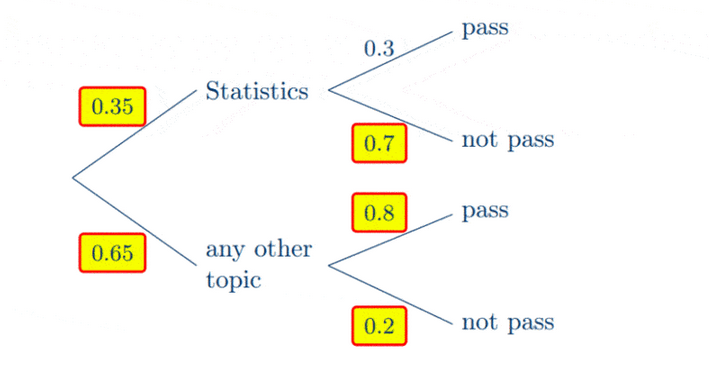
(b) Let $S=\{$ the topic is statistics $\}$
$O=\{$ the topic is any other $\}$,
$P=\{$ she passes the exam $\}$.
The paths highlighted in red represent the event that she does not pass the exam.

This diagram illustrates the Law of Total Probability as follows.
$
\begin{aligned}
\operatorname{Pr}\left(P^{\prime}\right) & =\operatorname{Pr}(S) \cdot \operatorname{Pr}\left(P^{\prime} \mid S\right)+\operatorname{Pr}(O) \cdot \operatorname{Pr}\left(P^{\prime} \mid O\right) \\
& =(0.35 \cdot 0.7)+(0.65 \cdot 0.2) \\
& =0.245+0.13 \\
& =0.375
\end{aligned}
$
