Question
A farmer owns a field in the shape of a triangle ABC such that AB = 650 m, AC = 1005 m
and BC = 1225 m
diagram not to scale
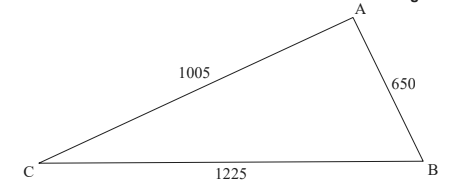
a. Find the size of AĈB. [3]
The local town is planning to build a highway that will intersect the borders of the field at points D and E, where DC = 210 m and CÊD = 100° , as shown in the diagram below.
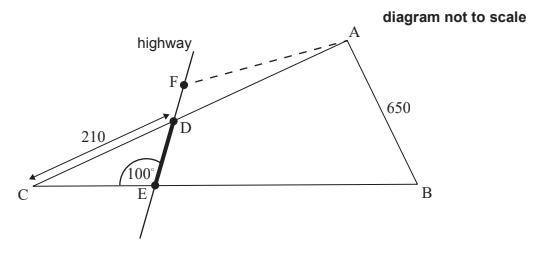
b. Find DE. [3]
The town wishes to build a carpark here. They ask the farmer to exchange the part of the field represented by triangle DCE. In return the farmer will get a triangle of equal area ADF, where F lies on the same line as D and E, as shown in the diagram above.
c. Find the area of triangle DCE. [5]
d. Estimate DF. You may assume the highway has a width of zero. [4]
Answer/Explanation
(a) cosine rule ACB = \(cos^{-1}(\frac{1005^{2}+1225^{2}-650^{2}}{2\times 1005\times 1225})\)
\(= 32.0 ((31.9980…)\) OR \(0.558 (0.558471…)\)
(b) sine rule \(\frac{DE}{sin31.9980..}= \frac{210}{sin100}\)
\(DE = 113 m (112.9937…)\)
(c) \(180-(100 +their part (a))=48.0019\) OR
\(0.837791…\(\frac{1}{2}\times 112.9937…\times 210\times sin48.002\)
\(8820m^{2}\rightarrow (8817.18 )\)
(d) \(1005 − 210 \) OR \(795\)
equating answer to part (c) to area of a triangle formula
\(8817.18..=\frac{1}{2}\times DF\times (1005-210)\times sin48.002..\)
\((DF=)29.8m(29.8473….)\)
Question
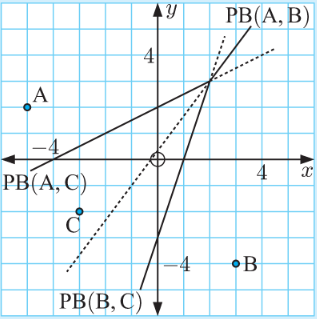
Construct a Voronoi diagram for the sites:
$\mathrm{A}(-5,2), \mathrm{B}(3,-4)$, and $\mathrm{C}(-3,-2)$
▶️Answer/Explanation
Sol:
The midpoint of $[\mathrm{AB}]$ is $\left(\frac{-5+3}{2}, \frac{2+-4}{2}\right)$ or $(-1,-1)$.
The gradient of $[\mathrm{AB}]$ is $\frac{-4-2}{3–5}=\frac{-6}{8}=-\frac{3}{4}$.
So, $\mathrm{PB}(\mathrm{A}, \mathrm{B})$ has gradient $\frac{4}{3}$ and passes through $(-1,-1)$.
The midpoint of $[\mathrm{AC}]$ is $\left(\frac{-5+-3}{2}, \frac{2+-2}{2}\right)$ or $(-4,0)$.
The gradient of $[\mathrm{AC}]$ is $\frac{-2-2}{-3–5}=\frac{-4}{2}=-2$.
So, $\mathrm{PB}(\mathrm{A}, \mathrm{C})$ has gradient $\frac{1}{2}$ and passes through $(-4,0)$.
The midpoint of $[\mathrm{BC}]$ is $\left(\frac{3+-3}{2}, \frac{-4+-2}{2}\right)$ or $(0,-3)$.
The gradient of $[\mathrm{BC}]$ is $\frac{-2–4}{-3-3}=\frac{2}{-6}=-\frac{1}{3}$.
So, $\mathrm{PB}(\mathrm{B}, \mathrm{C})$ has gradient 3 and passes through $(0,-3)$.
To draw the Voronoi diagram we plot the three sites on a set of axes. We can draw the perpendicular bisectors as dashed lines, then make solid only the parts which form the Voronoi edges.