Question
Sieun hits golf balls into the air. Each time she hits a ball she records θ , the angle at which the ball is launched into the air, and l , the horizontal distance, in metres, which the ball travels
from the point of contact to the first time it lands. The diagram below represents this information.
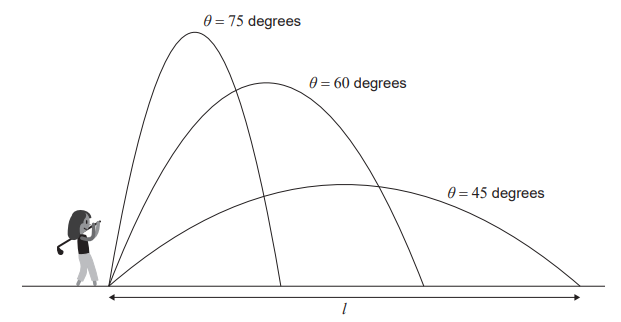
Sieun analyses her results and concludes:
\(\frac{dl}{d\Theta }=-0.2\Theta +9 , 35^{\circ}\leq \Theta \leq 75^{\circ}\)
(a)Determine whether the graph of l against θ is increasing or decreasing at θ = 50° . [3]
(b)Sieun observes that when the angle is 40°, the ball will travel a horizontal distance of 205.5 m.
(c)Find an expression for the function l (θ ) . [5]
Answer/Explanation
(a) \({I}′(50) = – 0.2 × 50 – 9\)
\(= −1 \)
the curve is decreasing at θ = 50°
(b) recognition of need to integrate (e.g. reverse power rule or integral symbol or integrating at least one term correctly)
\(l(\Theta )= -0.1\Theta ^{2}+ 9 \Theta +c\)
\(205.5=-0.1\times (40)^{2}+ 9\times (40)+c \)
\(c= 5.5 \)
\(l(\Theta )=-1.10+ 9\Theta +5.5\)
Question
The front view of a doghouse is made up of a square with an isosceles triangle on top. The doghouse is 1.35 m high and 0.9m wide, and sits on a square base.
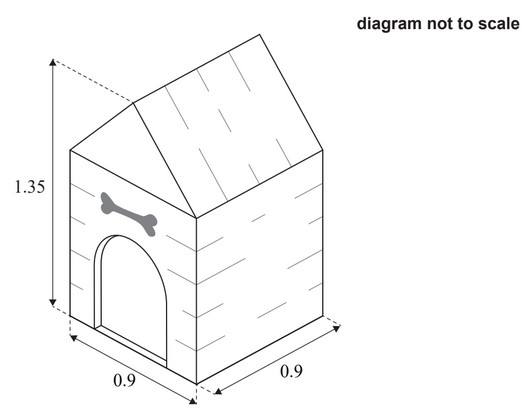
The top of the rectangular surfaces of the roof of the doghouse are to be painted
Find the area to be painted.
Answer/Explanation
Ans:
height of triangle at roof = 1.35 – 0.9 = 0.45
slant height = \(\sqrt{0.45^2 + 0.45^2}\) OR \(sin(45^o)=\frac{0.45}{slant height}\)
\(=\sqrt{0.405}(0.636396…, 0.45 \sqrt{2}\)
area of one rectangle on roof = \(\sqrt{0.405} \times 0.9 (=0.572756…)\)
area painted = \((2 \times \sqrt{0.405} \times 0.9 = 2 \times 0.572756…)\)
1.15 \(m^2\) (1.14551… \(m^2\), 0.81 \(\sqrt{2} m^2 \))
