Question
A quadratic function, \(f(x) = a{x^2} + bx\), is represented by the mapping diagram below.
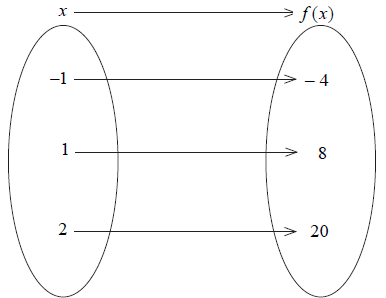
Use the mapping diagram to write down two equations in terms of a and b.
Find the value of a.
Find the value of b.
Calculate the x-coordinate of the vertex of the graph of f (x).
Answer/Explanation
Markscheme
4a + 2b = 20
a + b = 8 (A1)
a – b = –4 (A1) (C2)
Note: Award (A1)(A1) for any two of the given or equivalent equations.
[2 marks]
a = 2 (A1)(ft)
[1 mark]
b = 6 (A1)(ft) (C2)
Note: Follow through from their (a).
[1 mark]
\(x = – \frac{6}{{2(2)}}\) (M1)
Note: Award (M1) for correct substitution in correct formula.
\( = -1.5\) (A1)(ft) (C2)
[2 marks]
Question
The length of a square garden is (x + 1) m. In one of the corners a square of 1 m length is used only for grass. The rest of the garden is only for planting roses and is shaded in the diagram below.
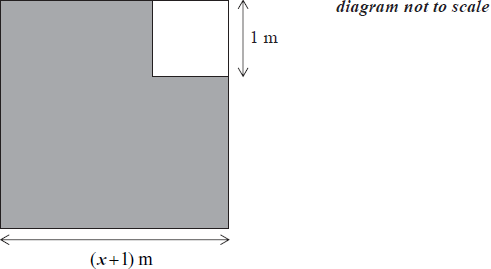
The area of the shaded region is A .
Write down an expression for A in terms of x.
Find the value of x given that A = 109.25 m2.
The owner of the garden puts a fence around the shaded region. Find the length of this fence.
Answer/Explanation
Markscheme
(x + 1)2 – 1 or x2 + 2x (A1) (C1)
[1 mark]
(x + 1)2 – 1 = 109.25 (M1)
x2 + 2x – 109.25 = 0 (M1)
Notes: Award (M1) for writing an equation consistent with their expression in (a) (accept equivalent forms), (M1) for correctly removing the brackets.
OR
(x + 1)2 – 1 = 109.25 (M1)
x + 1 = \(\sqrt {110.25} \) (M1)
Note: Award (M1) for writing an equation consistent with their expression in (a) (accept equivalent forms), (M1) for taking the square root of both sides.
OR
(x + 1)2 – 10.52 = 0 (M1)
(x – 9.5) (x + 11.5) = 0 (M1)
Note: Award (M1) for writing an equation consistent with their expression in (a) (accept equivalent forms), (M1) for factorised left side of the equation.
x = 9.5 (A1)(ft) (C3)
Note: Follow through from their expression in part (a).
The last mark is lost if x is non positive.
If the follow through equation is not quadratic award at most (M1)(M0)(A1)(ft).
[3 marks]
4 × (9.5 + 1) = 42 m (M1)(A1)(ft) (C2)
Notes: Award (M1) for correct method for finding the length of the fence. Accept equivalent methods.
[2 marks]
Question
Consider the function \(f(x) = 1.25 – {a^{ – x}}\) , where a is a positive constant and \(x \geqslant 0\). The diagram shows a sketch of the graph of \(f\) . The graph intersects the \(y\)-axis at point A and the line \(L\) is its horizontal asymptote.

Find the \(y\)-coordinate of A .
The point \((2{\text{, }}1)\) lies on the graph of \(y = f(x)\) . Calculate the value of \(a\) .
The point \((2{\text{, }}1)\) lies on the graph of \(y = f(x)\) . Write down the equation of \(L\) .
Answer/Explanation
Markscheme
\(y = 1.25 – {a^0}\) \(1.25 – 1\) (M1)
\(= 0.25\) (A1) (C2)
Note: Award (M1)(A1) for \((0{\text{, }}0.25)\) .
[2 marks]
\(1 = 1.25 – {a^{ – 2}}\) (M1)
\(a = 2\) (A1) (C2)
[2 marks]
\(y = 1.25\) (A1)(A1) (C2)
Note: Award (A1) for \(y =\) “a constant”, (A1) for \(1.25\).
[2 marks]
Question
Given that \(z = \frac{{12\cos (A)}}{{4q + r}}\) and that \(A = {60^ \circ }\), \(q = 8\) and \(r = 32\);
Find the exact value of \(z\).
Write your answer to part (a) correct to 2 decimal places.
Write your answer to part (a) correct to three significant figures.
Write your answer to part (a) in the form \(a \times {10^k}\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .
Answer/Explanation
Markscheme
\(z = \frac{{12\cos ({{60}^ \circ })}}{{(4(8) + 32)}}\) (M1)
Note: Award (M1) for correct substituted formula seen.
\( = 0.09375\left( {\frac{3}{{32}}} \right)\) (A1)(C2)
[2 marks]
\(0.09\) (A1)(ft) (C1)
[1 mark]
\(0.0938\) (A1)(ft) (C1)
[1 mark]
\(9.375 \times {10^{ – 2}}\) (\(9.38 \times {10^{ – 2}}\)) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for \(9.375\), (A1)(ft) for \( \times {10^{ – 2}}\). Follow through from their part (a).
[2 marks]
Question
The \(x\)-coordinate of the minimum point of the quadratic function \(f(x) = 2{x^2} + kx + 4\) is \(x =1.25\).
(i) Find the value of \(k\) .
(ii) Calculate the \(y\)-coordinate of this minimum point.
Sketch the graph of \(y = f(x)\) for the domain \( – 1 \leqslant x \leqslant 3\).
Answer/Explanation
Markscheme
(i) \(1.25 = – \frac{k}{{2(2)}}\) (M1)
OR
\(f'(x) = 4x + k = 0\) (M1)
Note: Award (M1) for setting the gradient function to zero.
\(k = – 5\) (A1) (C2)
(ii) \(2{(1.25)^2} – 5(1.25) + 4\) (M1)
\( = 0.875\) (A1)(ft) (C2)
Note: Follow through from their \(k\).
[4 marks]
(A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for a curve with correct concavity consistent with their \(k\) passing through (0, 4).
(A1)(ft) for minimum in approximately the correct place. Follow through from their part (a).
[2 marks]
Question
The function \(g(x)\) is defined as \(g(x) = 16 + k({c^{ – x}})\) where \(c > 0\) .
The graph of the function \(g\) is drawn below on the domain \(x \geqslant 0\) .
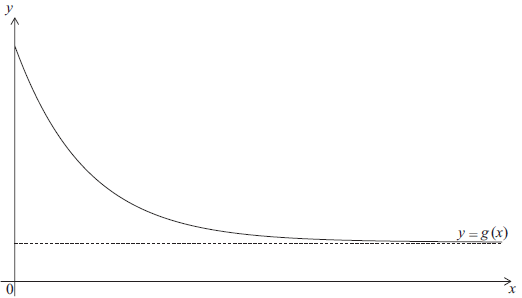
The graph of \(g\) intersects the y-axis at (0, 80) .
Find the value of \(k\) .
The graph passes through the point (2, 48) .
Find the value of \(c\) .
The graph passes through the point (2, 48) .
Write down the equation of the horizontal asymptote to the graph of \(y = g(x)\) .
Answer/Explanation
Markscheme
\(80 = 16 + k({c^0})\) (M1)
\(k = 64\) (A1) (C2)
[2 marks]
\(48 = 16 + 64({c^{ – 2}})\) (M1)
Note: Award (M1) for substitution of their \(k\) and (2, 48) into the equation for \(g(x)\).
\(c = \sqrt 2 \) (\(1.41\)) (\(1.41421 \ldots \)) (A1)(ft) (C2)
Notes: Award (M1)(A1)(ft) for \(c = \pm \sqrt 2 \) . Follow through from their answer to part (a).
[2 marks]
\(y = 16\) (A1)(A1) (C2)
Note: Award (A1) for \(y = \) a constant, (A1) for \(16\).
[2 marks]
Question
A function f (x) = p×2x + q is defined by the mapping diagram below.
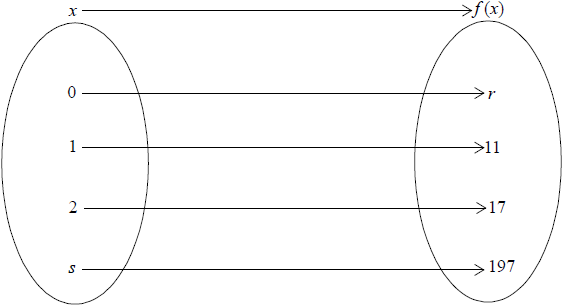
Find the value of
(i) p ;
(ii) q .
Write down the value of r .
Find the value of s .
Answer/Explanation
Markscheme
(i) 2p + q = 11 and 4p + q = 17 (M1)
Note: Award (M1) for either two correct equations or a correct equation in one unknown equivalent to 2p = 6 .
p = 3 (A1)
(ii) q = 5 (A1) (C3)
Notes: If only one value of p and q is correct and no working shown, award (M0)(A1)(A0).
[3 marks]
r = 8 (A1)(ft) (C1)
Note: Follow through from their answers for p and q irrespective of whether working is seen.
[1 mark]
3 × 2s + 5 = 197 (M1)
Note: Award (M1) for setting the correct equation.
s = 6 (A1)(ft) (C2)
Note: Follow through from their values of p and q.
[2 marks]
Question
Water has a lower boiling point at higher altitudes. The relationship between the boiling point of water (T) and the height above sea level (h) can be described by the model \(T = -0.0034h +100\) where T is measured in degrees Celsius (°C) and h is measured in metres from sea level.
Write down the boiling point of water at sea level.
Use the model to calculate the boiling point of water at a height of 1.37 km above sea level.
Water boils at the top of Mt. Everest at 70 °C.
Use the model to calculate the height above sea level of Mt. Everest.
Answer/Explanation
Markscheme
100 °C (A1) (C1)
[1 mark]
\(T = -0.0034 \times 1370 + 100\) (A1)(M1)
Note: Award (A1) for 1370 seen, (M1) for substitution of their h into the equation.
95.3 °C (95.342) (A1) (C3)
Notes: If their h is incorrect award at most (A0)(M1)(A0). If their h = 1.37 award at most (A0)(M1)(A1)(ft).
[3 marks]
\(70 = -0.0034h + 100\) (M1)
Note: Award (M1) for correctly substituted equation.
h = 8820 m (8823.52…) (A1) (C2)
Note: The answer is 8820 m (or 8.82 km.) units are required.
[2 marks]
Question
\(z = \frac{{17{x^2}}}{{a – b}}\).
Find the value of z when x = 12.5, a = 0.572 and b = 0.447. Write down your full calculator display.
Write down your answer to part (a)
(i) correct to the nearest 1000 ;
(ii) correct to three significant figures.
Write your answer to part (b)(ii) in the form a × 10k, where 1 ≤ a < 10, \(k \in \mathbb{Z}\).
Answer/Explanation
Markscheme
\(z = \frac{{17{{(12.5)}^2}}}{{(0.572 – 0.447)}}\) (M1)
Note: Award (M1) for correct substitution into formula.
= 21250 (A1) (C2)
[2 marks]
(i) 21000 (A1)(ft)
(ii) 21300 (A1)(ft) (C2)
Note: Follow through from part (a).
[2 marks]
\(2.13 \times 10^4\) (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for 2.13, (A1)(ft) for \(\times 10^4\). Follow through from part (b)(ii).
[ 2 marks]
Question
Consider the function \(f (x) = ax^3 − 3x + 5\), where \(a \ne 0\).
Find \(f ‘ (x) \).
Write down the value of \(f ′(0)\).
The function has a local maximum at x = −2.
Calculate the value of a.
Answer/Explanation
Markscheme
\( f ‘(x) = 3ax^2 – 3\) (A1)(A1) (C2)
Note: Award a maximum of (A1)(A0) if any extra terms are seen.
−3 (A1)(ft) (C1)
Note: Follow through from their part (a).
\(f ‘(x) = 0\) (M1)
Note: This may be implied from line below.
\(3a(-2)^2 – 3 = 0\) (M1)
\((a =) \frac{1}{4}\) (A1)(ft) (C3)
Note: Follow through from their part (a).
Question
The surface of a red carpet is shown below. The dimensions of the carpet are in metres.
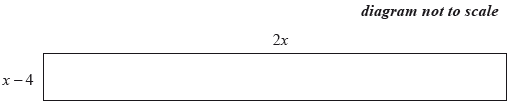
Write down an expression for the area, \(A\), in \({{\text{m}}^2}\), of the carpet.
The area of the carpet is \({\text{10 }}{{\text{m}}^2}\).
Calculate the value of \(x\).
The area of the carpet is \({\text{10 }}{{\text{m}}^2}\).
Hence, write down the value of the length and of the width of the carpet, in metres.
Answer/Explanation
Markscheme
\(2x(x – 4)\) or \(2{x^2} – 8x\) (A1) (C1)
Note: Award (A0) for \(x – 4 \times 2x\).
[1 mark]
\(2x(x – 4) = 10\) (M1)
Note: Award (M1) for equating their answer in part (a) to \(10\).
\({x^2} – 4x – 5 = 0\) (M1)
OR
Sketch of \(y = 2{x^2} – 8x\) and \(y = 10\) (M1)
OR
Using GDC solver \(x = 5\) and \(x = – 1\) (M1)
OR
\(2(x + 1)(x – 5)\) (M1)
\(x = 5{\text{ (m)}}\) (A1)(ft) (C3)
Notes: Follow through from their answer to part (a).
Award at most (M1)(M1)(A0) if both \(5\) and \(-1\) are given as final answer.
Final (A1)(ft) is awarded for choosing only the positive solution(s).
[3 marks]
\(2 \times 5 = 10{\text{ (m)}}\) (A1)(ft)
\(5 – 4 = 1{\text{ (m)}}\) (A1)(ft) (C2)
Note: Follow through from their answer to part (b).
Do not accept negative answers.
[2 marks]
Question
\(T = \frac{{\left( {\tan (2z) + 1} \right)\left( {2\cos (z) – 1} \right)}}{{{y^2} – {x^2}}}\), where \(x = 9\), \(y = 41\) and \(z = 30^\circ \).
Calculate the exact value of \(T\).
Give your answer to \(T\) correct to
(i) two significant figures;
(ii) three decimal places.
Pyotr estimates the value of \(T\) to be \(0.002\).
Calculate the percentage error in Pyotr’s estimate.
Answer/Explanation
Markscheme
\(\frac{{\left( {\tan (2 \times 30) + 1} \right)\left( {2\cos (30) – 1} \right)}}{{{{41}^2} – {9^2}}}\) (M1)
Note: Award (M1) for correct substitution into formula.
\( = 0.00125\;\;\;\left( {\frac{1}{{800}}} \right)\) (A1) (C2)
Note: Using radians the answer is \( – 0.000570502\), award at most (M1)(A0).
(i) \(0.0013\) (A1)(ft)
Note: Follow through from part (a).
(ii) \(0.001\) (A1)(ft) (C2)
Note: Follow through from part (a).
\(\left| {\frac{{0.002 – 0.00125}}{{0.00125}}} \right| \times 100\) (M1)
Notes: Award (M1) for their correct substitution into the percentage error formula. Absolute value signs are not required.
Their unrounded answer from part (a) must be used.
Do not accept use of answers from part (b).
\( = 60{\text{ (%)}}\) (A1)(ft) (C2)
Notes: The \({\text{%}}\) sign is not required.
The answer from radians is \(450.568{\text{%}}\), award (M1)(A1)(ft).
Follow through from part (a).
Question
An iron bar is heated. Its length, \(L\), in millimetres can be modelled by a linear function, \(L = mT + c\), where \(T\) is the temperature measured in degrees Celsius (°C).
At 150°C the length of the iron bar is 180 mm.
Write down an equation that shows this information.
At 210°C the length of the iron bar is 181.5 mm.
Write down an equation that shows this second piece of information.
At 210°C the length of the iron bar is 181.5 mm.
Hence, find the length of the iron bar at 40°C.
Answer/Explanation
Markscheme
\(180 = 150m + c\;\;\;\)(or equivalent) (A1) (C1)
\(181.5 = 210m + c\;\;\;\)(or equivalent) (A1) (C1)
\(m = 0.25,{\text{ }}c = 176.25\) (A1)(A1)(ft)
Note: Follow through from part (a) and part (b), irrespective of working shown.
\(L = 0.025(4) + 176.25\) (M1)
Note: Award (M1) for substitution of their \(m\), their \(c\) and 40 into equation.
\(L = 177\;\;\;(177.25){\text{ (mm)}}\) (A1)(ft) (C4)
Note: Follow through, within part (c), from their \(m\) and \(c\) only if working shown.
Question
A cuboid has a rectangular base of width \(x\) cm and length 2\(x\) cm . The height of the cuboid is \(h\) cm . The total length of the edges of the cuboid is \(72\) cm.
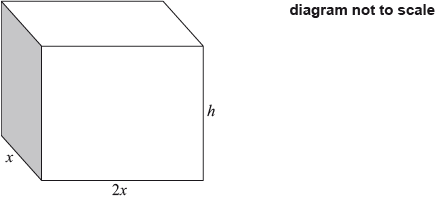
The volume, \(V\), of the cuboid can be expressed as \(V = a{x^2} – 6{x^3}\).
Find the value of \(a\).
Find the value of \(x\) that makes the volume a maximum.
Answer/Explanation
Markscheme
\(72 = 12x + 4h\;\;\;\)(or equivalent) (M1)
Note: Award (M1) for a correct equation obtained from the total length of the edges.
\(V = 2{x^2}(18 – 3x)\) (A1)
\((a = ){\text{ }}36\) (A1) (C3)
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 72x – 18{x^2}\) (A1)
\(72x – 18{x^2} = 0\;\;\;\)OR\(\;\;\;\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) (M1)
Notes: Award (A1) for \( – 18{x^2}\) seen. Award (M1) for equating derivative to zero.
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Note: Follow through from part (a).
OR
Sketch of \(V\) with visible maximum (M1)
Sketch with \(x \geqslant 0,{\text{ }}V \geqslant 0\) and indication of maximum (e.g. coordinates) (A1)(ft)
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Notes: Follow through from part (a).
Award (M1)(A1)(A0) for \((4,{\text{ }}192)\).
Award (C3) for \(x = 4,{\text{ }}y = 192\).
Question
The distance \(d\) from a point \({\text{P}}(x,{\text{ }}y)\) to the point \({\text{A}}(1,{\text{ }} – 2)\) is given by \(d = \sqrt {{{(x – 1)}^2} + {{(y + 2)}^2}} \)
Find the distance from \({\text{P}}(100,{\text{ }}200)\) to \({\text{A}}\). Give your answer correct to two decimal places.
Write down your answer to part (a) correct to three significant figures.
Write down your answer to part (b) in the form \(a \times {10^k}\), where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\).
Answer/Explanation
Markscheme
\(\sqrt {{{(100 – 1)}^2} + {{(200 + 2)}^2}} \) (M1)
\(\sqrt {50605} \;\;\;( = 224.955 \ldots )\) (A1)
Note: Award (M1)(A1) if \(\sqrt {50605} \) seen.
\({\text{224.96}}\) (A1) (C3)
Note: Award (A1) for their answer given correct to 2 decimal places.
\(225\) (A1)(ft) (C1)
Note: Follow through from their part (a).
\(2.25 \times {10^2}\) (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(A0) for \(2.25\) and an incorrect index value.
Award (A0)(A0) for answers such as \(22.5 \times {10^1}\).

