Question
The following graph shows the temperature in degrees Celsius of Robert’s cup of coffee, \(t\) minutes after pouring it out. The equation of the cooling graph is \(f (t) = 16 + 74 \times 2.8^{−0.2t}\) where \(f (t)\) is the temperature and \(t\) is the time in minutes after pouring the coffee out.
Robert, who lives in the UK, travels to Belgium. The exchange rate is 1.37 euros to one British Pound (GBP) with a commission of 3 GBP, which is subtracted before the exchange takes place. Robert gives the bank 120 GBP.
Find the initial temperature of the coffee.[1]
Write down the equation of the horizontal asymptote.[1]
Find the room temperature.[1]
Find the temperature of the coffee after 10 minutes.[1]
Find the temperature of Robert’s coffee after being heated in the microwave for 30 seconds after it has reached the temperature in part (d).[3]
Calculate the length of time it would take a similar cup of coffee, initially at 20°C, to be heated in the microwave to reach 100°C.[4]
Calculate correct to 2 decimal places the amount of euros he receives.[3]
He buys 1 kilogram of Belgian chocolates at 1.35 euros per 100 g.
Calculate the cost of his chocolates in GBP correct to 2 decimal places.[3]
Answer/Explanation
Markscheme
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
(UP) 90°C (A1)[1 mark]
y = 16 (A1)[1 mark]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
(UP) 16°C (ft) from answer to part (b) (A1)(ft)[1 mark]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
(UP) 25.4°C (A1)[1 mark]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
for seeing 20.75 or equivalent (A1)
for multiplying their (d) by their 20.75 (M1)
(UP) 42.8°C (A1)(ft)(G2)[3 marks]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
for seeing \(20 \times 2^{1.5t} = 100\) (A1)
for seeing a value of t between 1.54 and 1.56 inclusive (M1)(A1)
(UP) 1.55 minutes or 92.9 seconds (A1)(G3)[4 marks]
Financial accuracy penalty (FP) is applicable in part (ii) only.
\(120 – 3 = 117\)
(FP) \(117 \times 1.37\) (A1)
= 160.29 euros (correct answer only) (M1)
first (A1) for 117 seen, (M1) for multiplying by 1.37 (A1)(G2)[3 marks]
Financial accuracy penalty (FP) is applicable in part (ii) only.
(FP) \(\frac{{13.5}}{{1.37}}\) (A1)(M1)
9.85 GBP (answer correct to 2dp only)
first (A1) is for 13.5 seen, (M1) for dividing by 1.37 (A1)(ft)(G3)[3 marks]
Question
Give all answers in this question to the nearest whole currency unit.
Ying and Ruby each have 5000 USD to invest.
Ying invests his 5000 USD in a bank account that pays a nominal annual interest rate of 4.2 % compounded yearly. Ruby invests her 5000 USD in an account that offers a fixed interest of 230 USD each year.
Find the amount of money that Ruby will have in the bank after 3 years.[2]
Show that Ying will have 7545 USD in the bank at the end of 10 years.[3]
Find the number of complete years it will take for Ying’s investment to first exceed 6500 USD.[3]
Find the number of complete years it will take for Ying’s investment to exceed Ruby’s investment.[3]
Ruby moves from the USA to Italy. She transfers 6610 USD into an Italian bank which has an exchange rate of 1 USD = 0.735 Euros. The bank charges 1.8 % commission.
Calculate the amount of money Ruby will invest in the Italian bank after commission.[4]
Ruby returns to the USA for a short holiday. She converts 800 Euros at a bank in Chicago and receives 1006.20 USD. The bank advertises an exchange rate of 1 Euro = 1.29 USD.
Calculate the percentage commission Ruby is charged by the bank.[5]
Answer/Explanation
Markscheme
5000 + 3 × 230 = 5690 (M1)(A1)(G2)
Note: Accept alternative method.[2 marks]
\({\text{A}} = 5000{\left( {1 + \frac{{4.2}}{{100}}} \right)^{10}}\) or equivalent (M1)(A1)
\( = 7544.79 \ldots \) (A1)
\( = 7545{\text{ USD}}\) (AG)
Note: Award (M1) for correct substituted compound interest formula, (A1) for correct substitutions, (A1) for unrounded answer seen.
If final line not seen award at most (M1)(A1)(A0).[3 marks]
5000(1.042)n > 6500 (M1)(A1)
Notes: Award (M1) for setting up correct equation/inequality, (A1) for correct values.
Follow through from their formula in part (b).
OR
List of values seen with at least 2 terms (M1)
Lists of values including at least the terms with n = 6 and n = 7 (A1)
Note: Follow through from their formula in part (b).
OR
Sketch showing 2 graphs, one exponential, the other a horizontal line (M1)
Point of intersection identified or vertical line (M1)
Note: Follow through from their formula in part (b).
n = 7 (A1)(ft)(G2)[3 marks]
5000(1.042)n > 5000 + 230n (M1)(A1)
Note: Award (M1) for setting up correct equation/inequality, (A1) for correct values.
OR
2 lists of values seen (at least 2 terms per list) (M1)
Lists of values including at least the terms with n = 5 and n = 6 (A1)
Note: One of the lists may be written under (c).
OR
Sketch showing 2 graphs of correct shape (M1)
Point of intersection identified or vertical line (M1)
n = 6 (A1)(ft)(G2)
Note: Follow through from their formulae used in parts (a) and (b).[3 marks]
6610 × 0.735 (M1)
= 4858.35 (A1)
4858.35 × 0.982(= 4770.8997…) (M1)
= 4771 Euros (A1)(ft)(G3)
Note: Accept alternative method.[4 marks]
800 × 1.29 (= 1032 USD) (M1)(A1)
Note: Award (M1) for multiplying by 1.29, (A1) for 1032. Award (G2) for 1032 if product not seen.
(1032 – 1006.20 = 25.8)
\(25.8 \times \frac{100}{1032} \%\) (A1)(M1)
Note: Award (A1) for 25.8 seen, (M1) for multiplying by \(\frac{100}{1032}\).
OR
\(\frac{1006.20}{1032} = 0.975\) (M1)(A1)
OR
\(\frac{1006.20}{1032} \times 100 = 97.5\) (M1)(A1)
\( = 2.5{\text{ }}\% \) (A1)(G3)
Notes: If working not shown award (G3) for 2.5.
Accept alternative method.[5 marks]
Question
Give all answers in this question correct to two decimal places.
Part A
Estela lives in Brazil and wishes to exchange 4000 BRL (Brazil reals) for GBP (British pounds). The exchange rate is 1.00 BRL = 0.3071 GBP. The bank charges 3 % commission on the amount in BRL.
Give all answers in this question correct to two decimal places.
Part B
Daniel invests $1000 in an account that offers a nominal annual interest rate of 3.5 % compounded half yearly.
Find, in BRL, the amount of money Estela has after commission.[2]
Find, in GBP, the amount of money Estela receives.[2]
After her trip to the United Kingdom Estela has 400 GBP left. At the airport she changes this money back into BRL. The exchange rate is now 1.00 BRL = 0.3125 GBP.
Find, in BRL, the amount of money that Estela should receive.[2]
Estela actually receives 1216.80 BRL after commission.
Find, in BRL, the commission charged to Estela.[1]
The commission rate is t % . Find the value of t.[2]
Show that after three years Daniel will have $1109.70 in his account, correct to two decimal places.[3]
Write down the interest Daniel receives after three years.[1]
Answer/Explanation
Markscheme
4000 × 0.97 = 3880.00 (3880) (M1)(A1)(G2)
Note: Award (M1) for multiplication of correct numbers.
OR
3 % of 4000 = 120 (A1)
4000 – 120 = 3880.00 (3880) (A1)(G2)[2 marks]
3880 × 0.3071 = 1191.55 (M1)(A1)(ft)(G2)
Note: Award (M1) for multiplication of correct numbers. Follow through from their answer to part (a).[2 marks]
\(\frac{{400}}{{0.3125}}\) (M1)
= 1280.00 (1280) (A1)(G2)
Note: Award (M1) for division of correct numbers.[2 marks]
63.20 (A1)(ft)
Note: Follow through (their (c) –1216.80).[1 mark]
\(t = \frac{{63.20 \times 100}}{{1280}}\) (M1)
t = 4.94 (A1)(ft)(G2)
Note: Follow through from their answers to parts (c) and (d).[2 marks]
\({\text{A}} = 1000{\left( {1 + \frac{{3.5}}{{2 \times 100}}} \right)^6} = 1109.7023…\) (M1)(A1)(A1)
= 1109.70 (AG)
Notes: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for unrounded answer. If 1109.70 not seen award at most (M1)(A1)(A0).
OR
\({\text{I}} = 1000{\left( {1 + \frac{{3.5}}{{2 \times 100}}} \right)^6} – 1000 = 109.7023\) (M1)(A1)
A = 1109.7023… (A1)
= 1109.70 (AG)
Note: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for unrounded answer.[3 marks]
109.70 (A1)
Note: No follow through here.[1 mark]
Question
Give all answers in this question correct to two decimal places.
Arthur lives in London. On \({1^{{\text{st}}}}\) August 2008 Arthur paid \({\text{37}}\,{\text{500}}\) euros (\({\text{EUR}}\)) for a new car from Germany. The price of the same car in London was \({\text{34}}\,{\text{075}}\) British pounds (\({\text{GBP}}\)).
The exchange rate on \({1^{{\text{st}}}}\) August 2008 was \({\text{1}}\,{\text{EUR = 0.7234}}\,{\text{GBP}}\).
Calculate, in GBP, the price that Arthur paid for the car.[2]
Write down, in \({\text{GBP}}\), the amount of money Arthur saved by buying the car in Germany.[1]
Between \({1^{{\text{st}}}}\) August 2008 and \({1^{{\text{st}}}}\) August 2012 Arthur’s car depreciated at an annual rate of \(9\%\) of its current value.
Calculate the value, in \({\text{GBP}}\), of Arthur’s car on \({1^{{\text{st}}}}\) August 2009.[3]
Between \({1^{{\text{st}}}}\) August 2008 and \({1^{{\text{st}}}}\) August 2012 Arthur’s car depreciated at an annual rate of \(9\%\) of its current value.
Show that the value of Arthur’s car on \({1^{{\text{st}}}}\) August 2012 was \({\text{18}}\,{\text{600}}\,{\text{GBP}}\), correct to the nearest \({\text{100}}\,{\text{GBP}}\).[3]
Answer/Explanation
Markscheme
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(37\,500 \times 0.7234\) (M1)
\( = 27\,127.50\) (A1)(G2)[2 marks]
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(6947.50\) (A1)(ft)(G1)
Note: Follow through from part (a) irrespective of whether working is seen.[1 mark]
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(27\,127.50 \times 0.91\) (A1)(M1)
Note: Award (A1) for \(0.91\) seen or equivalent, (M1) for their \({\text{27}}\,{\text{127.50}}\) multiplied by \(0.91\)
OR
\(27\,127.50 – 0.09 \times 27\,127.50\) (A1)(M1)
Note: Award (A1) for \(0.09 \times 27\,127.50\) seen, and (M1) for \(27\,127.50 – 0.09 \times 27\,127.50\).
\( = 24\,686.03\) (A1)(ft)(G2)
Note: Follow through from part (a).[3 marks]
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(27\,127.50 \times {\left( {1 – \frac{9}{{100}}} \right)^4}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted compound interest formula, (A1)(ft) for correct substitution.
Follow through from part (a).
OR
\(27\,127.50 \times {(0.91)^4}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted geometric sequence formula, (A1)(ft) for correct substitution.
Follow through from part (a).
OR (lists (i))
\({\text{24}}\,{\text{686.03, 22}}\,{\text{464.28…, 20}}\,{\text{442.50…, 18}}\,{\text{602.67…}}\) (M1)(A1)(ft)
Notes: Award (M1) for at least the \({{\text{2}}^{{\text{nd}}}}\) term correct (calculated from their \(({\text{a}}) \times 0.91\)). Award (A1)(ft) for four correct terms (rounded or unrounded).
Follow through from part (a).
Accept list containing the last three terms only (\({\text{24}}\,{\text{686.03}}\) may be implied).
OR (lists(ii))
\(27\,127.50 – (2441.47… + 2221.74… + 2021.79… + 1839.82…)\) (M1)(A1)(ft)
Notes: Award (M1) for subtraction of four terms from \({\text{27}}\,{\text{127.50}}\).
Award (A1) for four correct terms (rounded or unrounded).
Follow through from part (a).
\( = 18\,602.67\) (A1)
\( = 18\,600\) (AG)
Note: The final (A1) is not awarded unless both the unrounded and rounded answers are seen.[3 marks]
Question
The following diagram shows a perfume bottle made up of a cylinder and a cone.
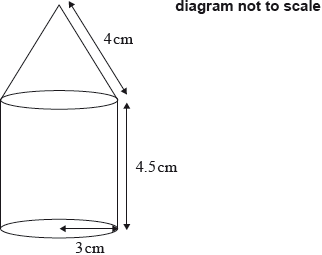
The radius of both the cylinder and the base of the cone is 3 cm.
The height of the cylinder is 4.5 cm.
The slant height of the cone is 4 cm.
(i) Show that the vertical height of the cone is \(2.65\) cm correct to three significant figures.
(ii) Calculate the volume of the perfume bottle.[6]
The bottle contains \({\text{125 c}}{{\text{m}}^{\text{3}}}\) of perfume. The bottle is not full and all of the perfume is in the cylinder part.
Find the height of the perfume in the bottle.[2]
Temi makes some crafts with perfume bottles, like the one above, once they are empty. Temi wants to know the surface area of one perfume bottle.
Find the total surface area of the perfume bottle.[4]
Temi covers the perfume bottles with a paint that costs 3 South African rand (ZAR) per millilitre. One millilitre of this paint covers an area of \({\text{7 c}}{{\text{m}}^{\text{2}}}\).
Calculate the cost, in ZAR, of painting the perfume bottle. Give your answer correct to two decimal places.[4]
Temi sells her perfume bottles in a craft fair for 325 ZAR each. Dominique from France buys one and wants to know how much she has spent, in euros (EUR). The exchange rate is 1 EUR = 13.03 ZAR.
Find the price, in EUR, that Dominique paid for the perfume bottle. Give your answer correct to two decimal places.[2]
Answer/Explanation
Markscheme
(i) \({x^2} + {3^2} = {4^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
Accept correct alternative method using trigonometric ratios.
\(x = 2.64575 \ldots \) (A1)
\(x = 2.65{\text{ }}({\text{cm}})\) (AG)
Note: The unrounded and rounded answer must be seen for the (A1) to be awarded.
OR
\(\sqrt {{4^2} – {3^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
\( = \sqrt 7 \) (A1)
\( = 2.65{\text{ (cm)}}\) (AG)
Note: The exact answer must be seen for the final (A1) to be awarded.
(ii) \(\pi \times {3^2} \times 4.5 + \frac{1}{3}\pi \times {3^2} \times 2.65\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula, (M1) for correct substitution into the volume of a cone formula, (M1) for adding both of their volumes.
\( = 152{\text{ c}}{{\text{m}}^3}\;\;\;(152.210 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}48.45\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G3)
\(\pi {3^2}h = 125\) (M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula.
Accept alternative methods. Accept \(4.43\) (\(4.42913 \ldots \)) from using rounded answers in \(h = \frac{{125 \times 4.5}}{{127}}\).
\(h = 4.42{\text{ (cm)}}\;\;\;\left( {4.42097 \ldots {\text{ (cm)}}} \right)\) (A1)(G2)
\(2\pi \times 3 \times 4.5 + \pi \times 3 \times 4 + \pi \times {3^2}\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into curved surface area of a cylinder formula, (M1) for correct substitution into the curved surface area of a cone formula, (M1) for adding the area of the base of the cylinder to the other two areas.
\( = 151{\text{ c}}{{\text{m}}^2}\;\;\;(150.796 \ldots {\text{ c}}{{\text{m}}^2},{\text{ }}48\pi {\text{ c}}{{\text{m}}^2})\) (A1)(G3)
\(\frac{{150.796 \ldots }}{7} \times 3\) (M1)(M1)
Notes: Award (M1) for dividing their answer to (c) by \(7\), (M1) for multiplying by \(3\). Accept equivalent methods.
\( = 64.63{\text{ (ZAR)}}\) (A1)(ft)(G2)
Notes: The (A1) is awarded for their correct answer, correctly rounded to 2 decimal places. Follow through from their answer to part (c). If rounded answer to part (c) is used the answer is \(64.71\) (ZAR).
\(\frac{{325}}{{13.03}}\) (M1)
Note: Award (M1) for dividing \(325\) by \(13.03\).
\( = 24.94{\text{ (EUR)}}\) (A1)(G2)
Note: The (A1) is awarded for the correct answer rounded to 2 decimal places, unless already penalized in part (d).
Question
Give your answers to parts (b), (c) and (d) to the nearest whole number.
Harinder has 14 000 US Dollars (USD) to invest for a period of five years. He has two options of how to invest the money.
Option A: Invest the full amount, in USD, in a fixed deposit account in an American bank.
The account pays a nominal annual interest rate of r % , compounded yearly, for the five years. The bank manager says that this will give Harinder a return of 17 500 USD.
Option B: Invest the full amount, in Indian Rupees (INR), in a fixed deposit account in an Indian bank. The money must be converted from USD to INR before it is invested.
The exchange rate is 1 USD = 66.91 INR.
The account in the Indian bank pays a nominal annual interest rate of 5.2 % compounded monthly.
Calculate the value of r.[3]
Calculate 14 000 USD in INR.[2]
Calculate the amount of this investment, in INR, in this account after five years.[3]
Harinder chose option B. At the end of five years, Harinder converted this investment back to USD. The exchange rate, at that time, was 1 USD = 67.16 INR.
Calculate how much more money, in USD, Harinder earned by choosing option B instead of option A.[3]
Answer/Explanation
Markscheme
\(17500 = 14000{\left( {1 + \frac{r}{{100}}} \right)^5}\) (M1)(A1)
Note: Award (M1) for substitution into the compound interest formula, (A1) for correct substitution. Award at most (M1)(A0) if not equated to 17500.
OR
N = 5
PV = ±14000
FV = \( \mp \)17500
P/Y = 1
C/Y = 1 (A1)(M1)
Note: Award (A1) for C/Y = 1 seen, (M1) for all other correct entries. FV and PV must have opposite signs.
= 4.56 (%) (4.56395… (%)) (A1) (G3)[3 marks]
14000 × 66.91 (M1)
Note: Award (M1) for multiplying 14000 by 66.91.
936740 (INR) (A1) (G2)
Note: Answer must be given to the nearest whole number.[2 marks]
\(936740 \times {\left( {1 + \frac{{5.2}}{{12 \times 100}}} \right)^{12 \times 5}}\) (M1)(A1)(ft)
Note: Award (M1) for substitution into the compound interest formula, (A1)(ft) for their correct substitution.
OR
N = 60
I% = 5.2
PV = ±936740
P/Y= 12
C/Y= 12 (A1)(M1)
Note: Award (A1) for C/Y = 12 seen, (M1) for all other correct entries.
OR
N = 5
I% = 5.2
PV = ±936740
P/Y= 1
C/Y= 12 (A1)(M1)
Note: Award (A1) for C/Y = 12 seen, (M1) for all other correct entries
= 1214204 (INR) (A1)(ft) (G3)
Note: Follow through from part (b). Answer must be given to the nearest whole number.[3 marks]
\(\frac{{1214204}}{{67.16}}\) (M1)
Note: Award (M1) for dividing their (c) by 67.16.
\(\left( {\frac{{1214204}}{{67.16}}} \right) – 17500 = 579\) (USD) (M1)(A1)(ft) (G3)
Note: Award (M1) for finding the difference between their conversion and 17500. Answer must be given to the nearest whole number. Follow through from part (c).[3 marks]

