Question
A store sells bread and milk. On Tuesday, 8 loaves of bread and 5 litres of milk were sold for $21.40. On Thursday, 6 loaves of bread and 9 litres of milk were sold for $23.40.
If \(b =\) the price of a loaf of bread and \(m =\) the price of one litre of milk, Tuesday’s sales can be written as \(8b + 5m = 21.40\).
Using simplest terms, write an equation in b and m for Thursday’s sales.[2]
Find b and m.[2]
Draw a sketch, in the space provided, to show how the prices can be found graphically.
[2]
Answer/Explanation
Markscheme
Thursday’s sales, \(6b + 9m = 23.40\) (A1)
\(2b + 3m = 7.80\) (A1) (C2)[2 marks]
\(m = 1.40\) (accept 1.4) (A1)(ft)
\(b = 1.80\) (accept 1.8) (A1)(ft)
Award (A1)(d) for a reasonable attempt to solve by hand and answer incorrect. (C2)[2 marks]
(A1)(A1)(ft)
(A1) each for two reasonable straight lines. The intersection point must be approximately correct to earn both marks, otherwise penalise at least one line.
Note: The follow through mark is for candidate’s line from (a). (C2)[2 marks]
Question
The number of cells, C, in a culture is given by the equation \(C = p \times 2^{0.5t} + q\), where t is the time in hours measured from 12:00 on Monday and p and q are constants.
The number of cells in the culture at 12:00 on Monday is 47.
The number of cells in the culture at 16:00 on Monday is 53.
Use the above information to write down two equations in p and q ;[2]
Use the above information to calculate the value of p and of q ;[2]
Use the above information to find the number of cells in the culture at 22:00 on Monday.[2]
Answer/Explanation
Markscheme
p + q = 47 (A1)
4p + q = 53 (A1) (C2)[2 marks]
Reasonable attempt to solve their equations (M1)
p = 2, q = 45 (A1) (C2)
Note: Accept only the answers p = 2, q = 45.[2 marks]
C = 2 × 20.5(10) + 45 (M1)
C = 109 (A1)(ft) (C2)
Note: Award (M1) for substitution of 10 into the formula with their values of p and q.[2 marks]
Question
Consider the function \(f(x) = p{(0.5)^x} + q\) where p and q are constants. The graph of f (x) passes through the points \((0,\,6)\) and \((1,\,4)\) and is shown below.
Write down two equations relating p and q.[2]
Find the value of p and of q.[2]
Write down the equation of the horizontal asymptote to the graph of f (x).[2]
Answer/Explanation
Markscheme
p + q = 6 (A1)
0.5p + q = 4 (A1) (C2)
Note: Accept correct equivalent forms of the equations.[2 marks]
p = 4, q = 2 (A1)(A1)(ft) (C2)
Notes: If both answers are incorrect, award (M1) for attempt at solving simultaneous equations.[2 marks]
y = 2 (A1)(A1)(ft) (C2)
Notes: Award (A1) for “y = a constant”, (A1)(ft) for 2. Follow through from their value for q as long as their constant is greater than 2 and less than 6.
An equation must be seen for any marks to be awarded.[2 marks]
Question
\(10 000\) people attended a sports match. Let \(x\) be the number of adults attending the sports match and \(y\) be the number of children attending the sports match.
Write down an equation in \(x\) and \(y\) .[1]
The cost of an adult ticket was \(12\) Australian dollars (AUD). The cost of a child ticket was \(5\) Australian dollars (AUD).
Find the total cost for a family of 2 adults and 3 children.[2]
The total cost of tickets sold for the sports match was \(108800{\text{ AUD}}\).
Write down a second equation in \(x\) and \(y\) .[1]
Write down the value of \(x\) and the value of \(y\) .[2]
Answer/Explanation
Markscheme
\(x + y = 10000\) (A1) (C1)[1 mark]
\(2 \times 12 + 3 \times 5\) (M1)
\(39{\text{ }}(39.0{\text{, }}39.00)\) (AUD) (A1) (C2)[2 marks]
\(12x + 5y = 108800\) (A1) (C1)[1 mark]
\(x = 8400\), \(y = 1600\) (A1)(ft)(A1)(ft) (C2)
Notes: Follow through from their equations. If \(x\) and \(y\) are both incorrect then award (M1) for attempting to solve simultaneous equations.[2 marks]
Question
A function f (x) = p×2x + q is defined by the mapping diagram below.
Find the value of
(i) p ;
(ii) q .[3]
Write down the value of r .[1]
Find the value of s .[2]
Answer/Explanation
Markscheme
(i) 2p + q = 11 and 4p + q = 17 (M1)
Note: Award (M1) for either two correct equations or a correct equation in one unknown equivalent to 2p = 6 .
p = 3 (A1)
(ii) q = 5 (A1) (C3)
Notes: If only one value of p and q is correct and no working shown, award (M0)(A1)(A0).[3 marks]
r = 8 (A1)(ft) (C1)
Note: Follow through from their answers for p and q irrespective of whether working is seen.[1 mark]
3 × 2s + 5 = 197 (M1)
Note: Award (M1) for setting the correct equation.
s = 6 (A1)(ft) (C2)
Note: Follow through from their values of p and q.[2 marks]
Question
The equation of a line L1 is \(2x + 5y = −4\).
Write down the gradient of the line L1.[1]
A second line L2 is perpendicular to L1.
Write down the gradient of L2.[1]
The point (5, 3) is on L2.
Determine the equation of L2.[2]
Lines L1 and L2 intersect at point P.
Using your graphic display calculator or otherwise, find the coordinates of P.[2]
Answer/Explanation
Markscheme
\(\frac{-2}{{5}}\) (A1) (C1)
\(\frac{5}{{2}}\) (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
\(3 = \frac{5}{2} \times 5 + c\) (M1)
Notes: Award (M1) for correct substitution of their gradient into equation of line. Follow through from their answer to part (b).
\(y = \frac{5}{2}x – \frac{19}{2}\) (A1)(ft)
OR
\(y – 3 = \frac{5}{2}(x – 5)\) (M1)(A1)(ft) (C2)
Notes: Award (M1) for correct substitution of their gradient into equation of line. Follow through from their answer to part (b).
(3, −2) (A1)(ft)(A1)(ft) (C2)
Notes: If parentheses not seen award at most (A0)(A1)(ft). Accept x = 3, y = −2. Follow through from their answer to part (c), even if no working is seen. Award (M1)(A1)(ft) for a sensible attempt to solve \(2x + 5y = −4\) and their \(y = \frac{5}{2}x – \frac{19}{2}\) or equivalent, simultaneously.
Question
A quadratic function \(f:x \mapsto a{x^2} + b\), where \(a\) and \(b \in \mathbb{R}\) and \(x \geqslant 0\), is represented by the mapping diagram.
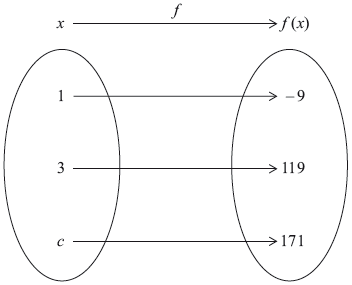
Using the mapping diagram, write down two equations in terms of \(a\) and \(b\).[2]
Solve the equations to find the value of
(i) \(a\);
(ii) \(b\).[2]
Find the value of \(c\).[2]
Answer/Explanation
Markscheme
\(a{(1)^2} + b = – 9\) (A1)
\(a{(3)^2} + b = 119\) (A1) (C2)
Note: Accept equivalent forms of the equations.[2 marks]
(i) \(a = 16\) (A1)(ft)
(ii) \(b = – 25\) (A1)(ft) (C2)
Note: Follow through from part (a) irrespective of whether working is seen.
If working is seen follow through from part (i) to part (ii).[2 marks]
\(16{c^2} – 25 = 171\) (M1)
Note: Award (M1) for correct quadratic with their \(a\) and \(b\) substituted.
\(c = 3.5\) (A1)(ft) (C2)
Note: Accept \(x\) instead of \(c\).
Follow through from part (b).
Award (A1) only, for an answer of \( \pm 3.5\) with or without working.[2 marks]
Question
The graph of the quadratic function \(f(x) = a{x^2} + bx + c\) intersects the y-axis at point A (0, 5) and has its vertex at point B (4, 13).
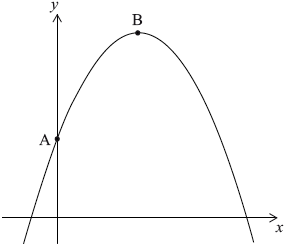
Write down the value of \(c\).[1]
By using the coordinates of the vertex, B, or otherwise, write down two equations in \(a\) and \(b\).[3]
Find the value of \(a\) and of \(b\).[2]
Answer/Explanation
Markscheme
5 (A1) (C1)[1 mark]
at least one of the following equations required
\(a{(4)^2} + 4b + 5 = 13\)
\(4 = – \frac{b}{{2a}}\)
\(a{(8)^2} + 8b + 5 = 5\) (A2)(A1) (C3)
Note: Award (A2)(A0) for one correct equation, or its equivalent, and (C3) for any two correct equations.
Follow through from part (a).
The equation \(a{(0)^2} + b(0) = 5\) earns no marks.[3 marks]
\(a = – \frac{1}{2},{\text{ }}b = 4\) (A1)(ft)(A1)(ft) (C2)
Note: Follow through from their equations in part (b), but only if their equations lead to unique solutions for \(a\) and \(b\).[2 marks]
Question
An iron bar is heated. Its length, \(L\), in millimetres can be modelled by a linear function, \(L = mT + c\), where \(T\) is the temperature measured in degrees Celsius (°C).
At 150°C the length of the iron bar is 180 mm.
Write down an equation that shows this information.[1]
At 210°C the length of the iron bar is 181.5 mm.
Write down an equation that shows this second piece of information.[1]
At 210°C the length of the iron bar is 181.5 mm.
Hence, find the length of the iron bar at 40°C.[4]
Answer/Explanation
Markscheme
\(180 = 150m + c\;\;\;\)(or equivalent) (A1) (C1)
\(181.5 = 210m + c\;\;\;\)(or equivalent) (A1) (C1)
\(m = 0.25,{\text{ }}c = 176.25\) (A1)(A1)(ft)
Note: Follow through from part (a) and part (b), irrespective of working shown.
\(L = 0.025(4) + 176.25\) (M1)
Note: Award (M1) for substitution of their \(m\), their \(c\) and 40 into equation.
\(L = 177\;\;\;(177.25){\text{ (mm)}}\) (A1)(ft) (C4)
Note: Follow through, within part (c), from their \(m\) and \(c\) only if working shown.
Question
A liquid is heated so that after \(20\) seconds of heating its temperature, \(T\) , is \({25^ \circ }{\text{C}}\) and after \(50\) seconds of heating its temperature is \({37^ \circ }{\text{C}}\) .
The temperature of the liquid at time \(t\) can be modelled by \(T = at + b\) , where \(t\) is the time in seconds after the start of heating.
Using this model one equation that can be formed is \(20a + b = 25\) .
Using the model, write down a second equation in \(a\) and \(b\) .[2]
Using your graphic display calculator or otherwise, find the value of \(a\) and of \(b\) .[2]
Use the model to predict the temperature of the liquid \(60{\text{ seconds}}\) after the start of heating.[2]
Answer/Explanation
Markscheme
\(50a + b = 37\) (A1)(A1) (C2)
Note: Award (A1) for \(50a + b\) , (A1) for \(= 37\) .
\(a = 0.4\), \(b = 17\) (A1)(ft)(A1)(ft) (C2)
Notes: Award (M1) for attempt to solve their equations if this is done analytically. If the GDC is used, award (ft) even if no working seen.
\(T = 0.4(60) + 17\) (M1)
Note: Award (M1) for correct substitution of their values and \(60\) into equation for \(T\).
\(T = 41{\text{ }}{{\text{(}}^ \circ }{\text{C}})\) (A1)(ft) (C2)
Note: Follow through from their part (b).

