Question
Ben inherits $6500. Ben invests his money in a bank that pays compound interest at a rate of 4.5% per annum.
Calculate the value of Ben’s investment at the end of 6 years. Give your answer correct to 2 decimal places.
Answer/Explanation
Markscheme
\({\text{Ben Amount}} = 6500{\left( {1 + \frac{{4.5}}{{100}}} \right)^6}\) (M1)(A1)
\( = $8464.69\) (A1)
(M1)(A1)(A0) if interest only found (=$1964.69) (C3)[3 marks]
Question
Charles invests \(3000{\text{ USD}}\) in a bank that offers compound interest at a rate of \(3.5\% \) per annum, compounded half-yearly.
Calculate the number of years that it takes for Charles’s money to double.
Answer/Explanation
Markscheme
\(6000 = 3000{\left( {1 + \frac{{3.5}}{{200}}} \right)^{2n}}\) (M1)(A1)
Note: (M1) for substituting values into a compound interest formula, (A1) for correct values with a variable for the power.
\(n = 20{\text{ years}}\) (A1) (C3)
Note: If \(n\) used in formula instead of \(2n\), can allow as long as final answer is halved to get \(20\).[3 marks]
Question
Emma places \({\text{€}}8000\) in a bank account that pays a nominal interest rate of \(5\% \) per annum, compounded quarterly.
Calculate the amount of money that Emma would have in her account after 15 years. Give your answer correct to the nearest Euro.[3]
After a period of time she decides to withdraw the money from this bank. There is \({\text{€}}9058.17\) in her account. Find the number of months that Emma had left her money in the account.[3]
Answer/Explanation
Markscheme
\(FV = 8000{(1.0125)^{60}}\) (M1)(A1)
Note: (M1) for substituting in compound interest formula, (A1) for correct substitution.
\({\text{€}}16857\) only (A1) (C3)[3 marks]
\(8000{(1.0125)^n} = 9058.17\) (M1)
Note: (M1) for equating compound interest formula to \(9058.17\)
\(n = 10\) correct answer only (A1)
So 30 months, (ft) on their \(n\) (A1)(ft) (C3)
Note: Award (C2) for \(2.5\) seen with no working.[3 marks]
Question
Eva invests \({\text{USD}}2000\) at a nominal annual interest rate of \(8\% \) compounded half-yearly.
Calculate the value of her investment after \(5\) years, correct to the nearest dollar.[3]
Toni invests \({\text{USD}}1500\) at an annual interest rate of \(7.8\% \) compounded yearly.
Find the number of complete years it will take for his investment to double in value.[3]
Answer/Explanation
Markscheme
\(2000{(1.04)^{10}}\) (M1)(A1)
Note: (M1) for substitution into CI formula. (A1) for correct substitution.
\(2960\) (A1)
Note: Award the final A1 for rounding their answer correctly to the nearest Yuan.
OR
\(2000{\left( {1 + \frac{8}{{200}}} \right)^{10}} – 2000\) (M1)(A1)
Note: (M1) for substitution into CI formula. (A1) for correct substitution.
\(2960\) (A1) (C3)
Note: Award the final A1 for rounding their answer correctly to the nearest Yuan.
\(1500{(1.078)^n} = 3000\) (M1)(M1)
Note: (M1) for correct substitution in CI formula, (M1) for \(3000\) seen.
\(n = 10{\text{ years}}\) (\(n = 9.23{\text{ years}}\) not accepted) (A1)
OR
\(1500{(1.078)^n} – 1500 = 1500\) (M1)(M1)
Note: (M1) for correct substitution in CI formula, (M1) for \(1500\) seen.
\(n = 10{\text{ years}}\) (\(n = 9.23{\text{ years}}\) not accepted) (A1)
OR
(M2) for list or graph. (M2)
\(n = 10{\text{ years}}\) (\(n = 9.23{\text{ years}}\) not accepted) (A1)
Note: If simple interest formula is used in both parts (a) and (b) then award (M0)(M0)(A0) in (a) and
(b) \(1500 = \frac{{1500(7.8)n}}{{100}}\) (M1)(A1)
(M1) for substitution in SI formula or lists, (A1) for correct substitution.
\(n = 13\) (A1) (C3)
Note: Correct answer only. If \(9.23\) seen without working award (A2).
Note: If calculator notation is used in either part with correct unrounded answer award (A1)(d) only if (FP) is applied in (a) or (AP) in (b). Otherwise (A2)(d) if penalty has already been applied in a previous question.
Question
An amount, C, of Australian Dollars (AUD) is invested for 5 years at 2.5 % yearly simple interest. The interest earned on this investment is 446.25 AUD.
5000 AUD is invested at a nominal annual interest rate of 2.5 % compounded half yearly.
Calculate the length of time in years for the interest on this investment to exceed 446.25 AUD.
Answer/Explanation
Markscheme
\(446.25 = 5000{\left( {1 + \frac{{2.5}}{{2(100)}}} \right)^{2n}} – 5000\) (M1)(A1)
Notes: Award (M1) for substitution into compound interest formula. Award (A1) for correct values.
\(5446.25 = 5000{\left( {1 + \frac{{2.5}}{{2(100)}}} \right)^{2n}}\) (A1)
n = 3.44
n = 3.5 (A1)
OR
5446.25 = 5000(1.0125)2n (A1)(M1)(A1)
Notes: Award (A1) for 5446.25 seen.
Award (M1) for substitution into compound interest formula.
Award (A1) for correct values.
n = 3.44 years
3.5 years required (A1) (C4)
Notes: For incorrect substitution into compound interest formula award at most (M1)(A0)(A1)(A0).
Award (A3) for 3.44 seen without working.
Allow solution by lists. In this case
Award (A1) for half year rate 1.25 % seen.
(A1) for 5446.25 seen.
(M1) for at least 2 correct uses of multiplication by 1.0125
5000 × 1.0125 = 5062.5 and 5062.5 × 1.0125 = 5125.78125
(A1) n = 3.5
If yearly rate used then award (A0)(A1)(M1)(A0)[4 marks]
Question
Inge borrows € 4500 for 2 years.
Bank 1 charges compound interest at a rate of 15 % per annum, compounded quarterly.
Calculate the total amount to be repaid at the end of the 2 years. Give your answer correct to two decimal places.
Answer/Explanation
Markscheme
Note: Financial penalty (FP) applies in this part
\(A = 4500{\left( {1 + \frac{{15}}{{400}}} \right)^{4 \times 2}}\) (M1)(A1)
Note: Award (M1) for substitution into CI formula, (A1) for correct substitution.
(FP) A = € 6041.12 (€ not required) (A1) (C3)[3 marks]
Question
Mr Tan invested 5000 Swiss Francs (CHF) in Bank A at an annual simple interest rate of r %, for four years. The total interest he received was 568 CHF.
Mr Black invested 5000 CHF in Bank B at a nominal annual interest rate of 3.6 %, compounded quarterly for four years.
Calculate the total interest he received at the end of the four years. Give your answer correct to two decimal places.
Answer/Explanation
Markscheme
Financial penalty (FP) applies in part (b).
\(I = 5000(1.009)^{16} – 5000\) (M1)(A1)
Note: Award (M1) for substitution into the compound interest formula, (A1) for correct values.
(FP) I = 770.70 CHF (A1) (C3)[3 marks]
Question
Astrid invests 1200 Euros for five years at a nominal annual interest rate of 7.2 %, compounded monthly.
Find the interest Astrid has earned during the five years of her investment. Give your answer correct to two decimal places.
Answer/Explanation
Markscheme
\(I = 1200{\left( {1 + \frac{{7.2}}{{600}}} \right)^{5 \times 12}} – 1200\) (M1)(A1)
I = 518.15 Euros (A1) (C3)
Notes: Award (M1) for substitution in the compound interest formula, (A1) for correct substitutions, (A1) for correct answer.
If final amount found is 1718.15 and working shown award (M1) (A1)(A0).[3 marks]
Question
Kunal borrows 200 000 Indian rupees (INR) from a money lender for 18 months at a nominal annual interest rate of \(15\% \), compounded monthly.
Calculate the total amount that Kunal must repay at the end of the 18 months. Give your answer to the nearest rupee.
Answer/Explanation
Markscheme
\(A = 200000{\left( {1 + \frac{{15}}{{100 \times 12}}} \right)^{1.5 \times 12}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.
\( = 250115.4788\) INR (A1)
\( = 250115\) INR (A1) (C4)
Note: Award final (A1) for their answer correct to the nearest rupee.[4 marks]
Question
Veronica wants to make an investment and accumulate 25 000 EUR over a period of 18 years. She finds two investment options.
Option 2 offers a nominal annual interest rate of 4 %, compounded monthly.
Find the amount that Veronica has to invest with option 2 to have 25 000 EUR in her account after 18 years. Give your answer correct to two decimal places.
Answer/Explanation
Markscheme
\({\text{C}} = {\left( {1 + \frac{{0.04}}{{12}}} \right)^{12 \times 18}} = 25000\) (M1)(A1)
Note: Award (M1) for substitution into a compound interest formula. Award (A1) for correct substitution and equation.
C =12183.39 (EUR) (A1) (C3)
Note: The final (A1) can only be given for seeing the correct figures.[3 marks]
Question
Jackson invested 12 000 Australian dollars (AUD) in a bank that offered simple interest at an annual interest rate of r %. The value of Jackson’s investment doubled after 20 years.
Maddison invests 15 000 AUD in a bank that offers compound interest at a nominal annual interest rate of 4.44 %, compounded quarterly.
Calculate the number of years that it will take for Maddison’s investment to triple in value.
Answer/Explanation
Markscheme
\(45000 = 15000{\left( {1 + \frac{{4.44}}{{400}}} \right)^{4n}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for a correctly substituted formula and correctly equated to 45 000.
OR
\(3= {\left( {1 + \frac{{4.44}}{{400}}} \right)^{4n}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for a correctly substituted formula and correctly equated to 3.
n = 25 years (A1) (C3)
Notes: Award (A1)(M0)(A0) if 24.9 or 24.88 seen as a final answer, with no working seen. Award, at most, (A1)(M1)(A0) if working is seen and a final answer of 24.9 or 24.88 is given.[3 marks]
Question
Jenny invested $20 000 in a bank account that paid 3.5 % annual simple interest. She withdrew her investment from the account when its value was $31 200.
Ramón invests $18 000 in a bank account that pays 3.4 % nominal annual interest, compounded quarterly.
Find the minimum number of years that Ramón must invest the money for his investment to be worth $27 000.
Answer/Explanation
Markscheme
\(27000 = 18000{\left[ {1 + \frac{{3.4}}{{100 \times 4}}} \right]^{4n}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.
\((n =) 12\) (A1) (C3)
Note: Correct answer only. If 11.976… seen award (A2).
Question
Marcus has been given 500 Australian dollars (AUD) by his grandmother for his 18th birthday.
He plans to deposit it in a bank which offers a nominal annual interest rate of 6.0 %, compounded quarterly, for three years.
Calculate the total amount of interest Marcus would earn, in AUD, over the three years. Give your answer correct to two decimal places.[3]
Marcus would earn the same amount of interest, compounded annually, for three years if he deposits the 500 AUD in a second bank.
Calculate the interest rate the second bank offers.[3]
Answer/Explanation
Markscheme
\(500{\left( {1 + \frac{6}{{100 \times 4}}} \right)^{4 \times 3}} – 500\) (M1)(A1)
Note: Award (M1) for substitution in correct formula (A1) for correct substitutions.
\(= 97.81\) (A1) (C3)
Note: The answer must be given to 2 dp or the final (A1) is not awarded.
\(97.8090… = 500{\left( {1 + \frac{r}{{100}}} \right)^3} – 500\) (M1)(A1)(ft)
Note: Award (M1) for substitution in correct formula, (A1)(ft) for their correct substitutions.
\(= 6.14\) (6.13635…) (A1)(ft) (C3)
Note: Follow through from their answer to part (a).
Question
Ludmila takes a loan of 320 000 Brazilian Real (BRL) from a bank for two years at a nominal annual interest rate of 10%, compounded half yearly.
Write down the number of times interest is added to the loan in the two years.[1]
Calculate the exact amount of money that Ludmila must repay at the end of the two years.[3]
Ludmila estimates that she will have to repay \({\text{360}}\,{\text{000}}\) BRL at the end of the two years.
Calculate the percentage error in her estimate.[2]
Answer/Explanation
Markscheme
4 (A1) (C1)[1 mark]
\(320\,000{\left( {1 + \frac{{10}}{{2 \times 100}}} \right)^{2 \times 2}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.
OR
\({\text{N}} = 2\)
\({\text{I}}\% = 10\)
\({\text{PV}} = – 320000\)
\({\text{P }}/{\text{ Y}} = 1\)
\({\text{C }}/{\text{ Y}} = 2\) (A1)(M1)
Note: Award (A1) for \({\text{C }}/{\text{ Y}} = 2\) seen, (M1) for correctly substituted values from the question into the finance application.
OR
\({\text{N}} = 4\)
\({\text{I}}\% = 10\)
\({\text{PV}} = – 320000\)
\({\text{P }}/{\text{ Y}} = 2\)
\({\text{C }}/{\text{ Y}} = 2\) (A1)(M1)
Note: Award (A1) for \({\text{C }}/{\text{ Y}} = 2\) seen, (M1) for correctly substituted values from the question into the finance application.
amount to repay \( = 388962\) (A1) (C3)
Note: Award (C2) for final answer \(389000\) if \(388962\) not seen previously.[3 marks]
\(\left| {\frac{{360\,000 – 388\,962}}{{388\,962}}} \right| \times 100\) (M1)
Note: Award (M1) for correctly substituted percentage error formula.
\( = 7.45{\text{ (% ) }}(7.44597 \ldots )\) (A1)(ft) (C2)
Notes: Follow through from their answer to part (b).[2 marks]
Question
Mandzur, a farmer, takes out a loan to buy a buffalo. He borrows 900 000 Cambodian riels (KHR) for 2 years. The nominal annual interest rate is 15%, compounded monthly.
Find the amount of the interest that Mandzur must pay. Give your answer correct to the nearest 100 KHR.[4]
Write down your answer to part (a) in the form \(a \times {10^k},{\text{ where }}1 \leqslant a < 10,{\text{ }}k \in \mathbb{Z}\).[2]
Answer/Explanation
Markscheme
\(FV = 900000{\left( {1 + \frac{{15}}{{12 \times 100}}} \right)^{24}}\) (M1)(A1)
Note: Award (M1) for substitution in the compound interest formula (either \(FV\) or interest), do not penalize if \(–PV\) not seen.
Award (A1) for correct substitution.
OR
\({\text{N}} = 2\)
\({\text{I% = 15}}\)
\({\text{PV = 900}}\,{\text{000}}\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 12\) (A1)(M1)
Note: Award (A1) for \({\text{C/Y}} = 12\) seen, (M1) for other correct entries.
OR
\({\text{N}} = 24\)
\({\text{I% = 15}}\)
\({\text{PV = 900}}\,{\text{000}}\)
\({\text{P/Y}} = 12\)
\({\text{C/Y}} = 12\) (A1)(M1)
Note: Award (A1) for \({\text{C/Y}} = 12\) seen, (M1) for other correct entries.
\({\text{interest = 321615.945}}\) (A1)
\( = 312\,600\;\;\;{\text{(KHR)}}\) (A1)(ft) (C4)
Notes: Award the final (A1) for the correct rounding of their unrounded answer.
If final amount is \(1 212 600\) and working is shown award (M1)(A1)(A0)(A1)(ft).
Award (A2) for \((FV = )\ 1212600\) if no working is seen.
\(3.126 \times {10^5}\) (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for their \(3.126\) \((3.13)\), (A1)(ft) for \( \times {10^5}\).
Follow through from part (a).
Question
Pierre invests 5000 euros in a fixed deposit that pays a nominal annual interest rate of 4.5%, compounded monthly, for seven years.
Calculate the value of Pierre’s investment at the end of this time. Give your answer correct to two decimal places.[3]
Carla has 7000 dollars to invest in a fixed deposit which is compounded annually.
She aims to double her money after 10 years.
Calculate the minimum annual interest rate needed for Carla to achieve her aim.[3]
Answer/Explanation
Markscheme
\(5000{\left( {1 + \frac{{4.5}}{{12 \times 100}}} \right)^{12 \times 7}}\) (M1)(A1)
Note: Award (M1) for substitution into compound interest formula, (A1) for correct substitutions.
OR
\(N = 7\)
\(I\% = 4.5\)
\(PV = ( \pm )5000\)
\(P/Y = 1\)
\(C/Y = 12\) (A1)(M1)
Note: Award (A1) for \(C/Y = 12\) seen, (M1) for all other correct entries.
OR
\(N = 84\)
\(I\% = 4.5\)
\(PV = ( \pm )5000\)
\(P/Y = 12\)
\(C/Y = 12\) (A1)(M1)
Note: Award (A1) for \(C/Y = 12\) seen, (M1) for all other correct entries.
\( = 6847.26{\text{ (euros)}}\) (A1) (C3)
Note: Answer must be correct to 2 decimal places for the final (A1) to be awarded.
\(14000 = 7000{\left( {1 + \frac{r}{{100}}} \right)^{10}}\) (M1)(A1)
Notes: Award (M1) for substitution into compound interest formula equated to 14000 or equivalent.
Award (A1) for correct substitutions.
OR
\(N = 10\)
\(PV = \pm 7000\)
\(FV \mp 14000\)
\(P/Y = 1\)
\(C/Y = 1\) (A1)(M1)
Note: Award (A1) for \(C/Y = 1\) seen, (M1) for other correct entries. \(PV\) and \(FV\) must have opposite signs.
\(r = 7.18\% \;\;\;(7.17734 \ldots \% ,{\text{ }}0.0718)\) (A1) (C3)
Note: Do not penalize if \(\%\) sign is missing. Do not accept \(0.0718\%\).
Question
Minta deposits 1000 euros in a bank account. The bank pays a nominal annual interest rate of 5%, compounded quarterly.
Find the amount of money that Minta will have in the bank after 3 years. Give your answer correct to two decimal places.[3]
Minta will withdraw the money from her bank account when the interest earned is 300 euros.
Find the time, in years, until Minta withdraws the money from her bank account.[3]
Answer/Explanation
Markscheme
\(1000{\left( {1 + \frac{5}{{4 \times 100}}} \right)^{4 \times 3}}\) (M1)(A1)
Note: Award (M1) for substitution into compound interest formula, (A1) for correct substitution.
OR
\({\text{N}} = 3\)
\({\text{I}}\% = 5\)
\({\text{PV}} = – 1000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 4\) (A1)(M1)
Note: Award (A1) for \({\text{C/Y}} = 4\) seen, (M1) for other correct entries.
OR
\({\text{N}} = 12\)
\({\text{I}}\% = 5\)
\({\text{PV}} = – 1000\)
\({\text{P/Y}} = 4\)
\({\text{C/Y}} = 4\) (A1)(M1)
Note: Award (A1) for \({\text{C/Y}} = 4\) seen, (M1) for other correct entries.
\( = 1160.75\) (€) (A1) (C3)
\(1000{\left( {1 + \frac{5}{{4 \times 100}}} \right)^{4 \times t}} = 1300\) (M1)(A1)
Note: Award (M1) for using the compound interest formula with a variable for time, (A1) for substituting correct values and equating to \(1300\).
OR
\({\text{I}}\% = 5\)
\({\text{PV}} = \pm 1000\)
\({\text{FV}} = \mp 1300\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 4\) (A1)(M1)
Note: Award (A1) for 1300 seen, (M1) for the other correct entries.
OR
\({\text{I}}\% = 5\)
\({\text{PV}} = \pm 1000\)
\({\text{FV}} = \mp 1300\)
\({\text{P/Y}} = 4\)
\({\text{C/Y}} = 4\) (A1)(M1)
Note: Award (A1) for 1300 seen, (M1) for the other correct entries.
OR
Sketch drawn of two appropriate lines which intersect at a point
Note: Award (M1) for a sketch with a straight line intercepted by appropriate curve, (A1) for a numerical answer in the range \(5.2-5.6\).
\(t = 5.28{\text{ (years)}}\;\;\;(5.28001 \ldots )\) (A1) (C3)
Question
Gabriella purchases a new car.
The car’s value in dollars, \(V\), is modelled by the function
\[V(t) = 12870 – k{(1.1)^t},{\text{ }}t \geqslant 0\]
where \(t\) is the number of years since the car was purchased and \(k\) is a constant.
After two years, the car’s value is $9143.20.
This model is defined for \(0 \leqslant t \leqslant n\). At \(n\) years the car’s value will be zero dollars.
Write down, and simplify, an expression for the car’s value when Gabriella purchased it.[2]
Find the value of \(k\).[2]
Find the value of \(n\).[2]
Answer/Explanation
Markscheme
\(12870 – k{(1.1)^0}\) (M1)
Note: Award (M1) for correct substitution into \(V(t)\).
\( = 12870 – k\) (A1) (C2)
Note: Accept \(12870 – 3080\) OR 9790 for a final answer.[2 marks]
\(9143.20 = 12870 – k{(1.1)^2}\) (M1)
Note: Award (M1) for correct substitution into \(V(t)\).
\((k = ){\text{ }}3080\) (A1) (C2)[2 marks]
\(12870 – 3080{(1.1)^n} = 0\) (M1)
Note: Award (M1) for correct substitution into \(V(t)\).
OR
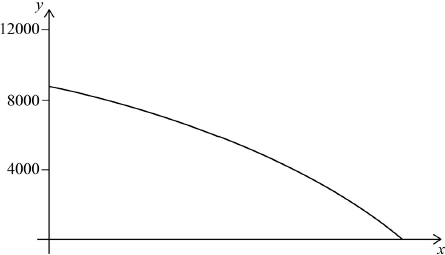 (M1)
(M1)
Note: Award (M1) for a correctly shaped curve with some indication of scale on the vertical axis.
\((n = ){\text{ }}15.0{\text{ }}(15.0033 \ldots )\) (A1)(ft) (C2)
Note: Follow through from part (b).[2 marks]
Question
Juan buys a bicycle in a sale. He gets a discount of 30% off the original price and pays 560 US dollars (USD).
To buy the bicycle, Juan takes a loan of 560 USD for 6 months at a nominal annual interest rate of 75%, compounded monthly. Juan believes that the total amount he will pay will be less than the original price of the bicycle.
Calculate the original price of the bicycle.[2]
Calculate the difference between the original price of the bicycle and the total amount Juan will pay.[4]
Answer/Explanation
Markscheme
\(\frac{{560}}{{70}} \times 100\) (or equivalent) (M1)
Note: Award (M1) for dividing 560 by 0.7 or equivalent.
\( = 800{\text{ (USD)}}\) (A1) (C2)[2 marks]
\(560{\left( {1 + \frac{{75}}{{12 \times 100}}} \right)^{12 \times \frac{1}{2}}}\) (M1)(A1)
Note: Award (M1) for substitution into interest formula, (A1) for their correct substitution.
OR
\({\text{N}} = \frac{1}{2}\)
\({\text{I% }} = 75\)
\({\text{PV}} = ( \pm )560\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 12\) (A1)(M1)
Note: Award (A1) for \({\text{C/Y}} = 12\) seen, (M1) for all other entries correct.
OR
\({\text{N}} = 6\)
\({\text{I% }} = 75\)
\({\text{PV}} = ( \pm )560\)
\({\text{P/Y}} = 12\)
\({\text{C/Y}} = 12\) (A1)(M1)
Note: Award (A1) for \({\text{C/Y}} = 12\) seen, (M1) for all other entries correct.
\( = 805.678 \ldots {\text{ (USD)}}\) (A1)
Note: Award (A3) for 805.678… (806) seen without working.
(Juan spends) 5.68 (USD) (5.67828… USD) (more than the original price) (A1)(ft) (C4)[4 marks]
Question
The following table shows four different sets of numbers: \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
Complete the second column of the table by giving one example of a number from each set.[4]
Josh states: “Every integer is a natural number”.
Write down whether Josh’s statement is correct. Justify your answer.[2]
Answer/Explanation
Markscheme
(A1)(A1)(A1)(A1)(C4)[4 marks]
Incorrect (A1)
Natural numbers are positive integers. Integers can also be negative. (or equivalent) (R1) (C2)
Note: Accept a correct justification. Do not award (R0)(A1).
Accept: a statement with an example of an integer which is not natural.[2 marks]
Question
Yun Bin invests \(5000{\text{ euros}}\) in an account which pays a nominal annual interest rate of \(6.25\% \) , compounded monthly.
Give all answers correct to two decimal places.
Find the value of the investment after 3 years.[3]
Find the difference in the final value of the investment if the interest was compounded quarterly at the same nominal rate.[3]
Answer/Explanation
Markscheme
\(FV = 5000{\left( {1 + \frac{{6.25}}{{1200}}} \right)^{3 \times 12}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.
OR
\(N = 3\)
\(I\% = 6.25\)
\(PV = – 5000\)
\(P/Y = 1\)
\(C/Y = 12\) (M1)(A1)
Note: Award (A1) for \(C/Y = 12\) seen, (M1) for other correct entries.
OR
\(N = 36\)
\(I\% = 6.25\)
\(PV = – 5000\)
\(P/Y = 12\)
\(C/Y = 12\) (M1)(A1)
Note: Award (A1) for \(C/Y = 12\) seen, (M1) for other correct entries.
\( = 6028.22\) (A1) (C3)
Note: The answer should be given correct to two decimal places or the final (A1) is not awarded.
\(FV = 5000{\left( {1 + \frac{{6.25}}{{400}}} \right)^{3 \times 4}}\) (M1)
Note: Award (M1) for correctly substituted compound interest formula.
OR
\(N = 3\)
\(I\% = 6.25\)
\(PV = – 5000\)
\(P/Y = 1\)
\(C/Y = 4\) (M1)
Note: Award (M1) for all correct entries seen.
OR
\(N = 12\)
\(I\% = 6.25\)
\(PV = – 5000\)
\(P/Y = 4\)
\(C/Y = 4\) (M1)
Note: Award (M1) for all correct entries seen.
\(FV = 6022.41\) (A1)
\({\text{Difference}} = 5.80\) (A1)(ft) (C3)
Notes: Accept \(5.81\). This answer should be given correct to two decimal places or the final (A1) is not awarded unless this has already been penalized in part (a). Follow through from part (a).
Notes: Illustrating use of GDC notation acceptable in this case only. However on P2 an answer given with no working would receive G2.

