Download IITian Academy App for accessing Online Mock Tests and More..
Question
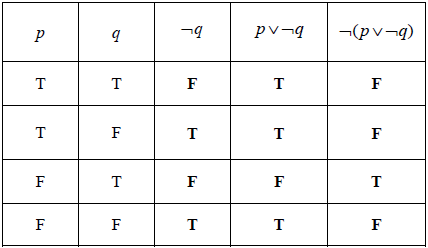
The truth table below shows the truth-values for the proposition
\(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q \Rightarrow \neg {\text{ }}p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } \neg q\)
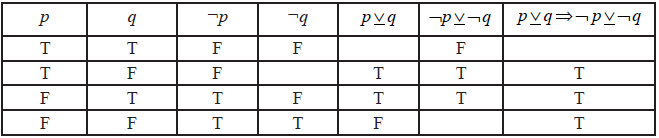
Explain the distinction between the compound propositions, \(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q\) and \(p \vee q\).[1]
Fill in the four missing truth-values on the table.[4]
State whether the proposition \(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q \Rightarrow \neg p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } \neg q\) is a tautology, a contradiction or neither.[1]
Answer/Explanation
Markscheme
Both are ‘p or q’, the first is ‘but not both’ (A1)
Note: Award mark for clear understanding if wording is poor. (C1)[1 mark]
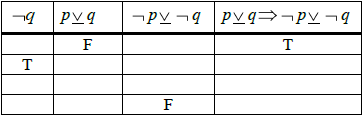(A1)(A1)(ft)(A1)(A1)
Note: Follow through is for final column. (C4)[4 marks]
Tautology. (A1)(ft) (C1)[1 mark]
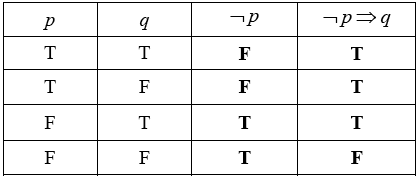
Question
(i) Complete the truth table below.
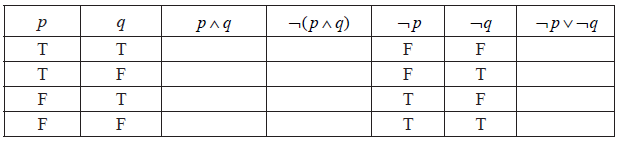
(ii) State whether the compound propositions \(\neg (p \wedge q)\) and \(\neg p \vee \neg q\) are equivalent.[4]
Consider the following propositions.
\(p:{\text{ Amy eats sweets}}\)
\(q:{\text{ Amy goes swimming.}}\)
Write, in symbolic form, the following proposition.
Amy either eats sweets or goes swimming, but not both.[2]
Answer/Explanation
Markscheme
(i)
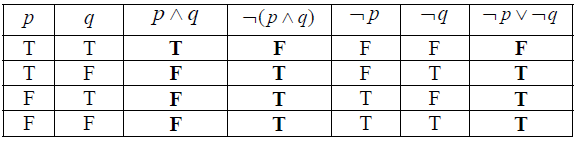(A3)
Note: Award (A1) for \(p \wedge q\) column correct, (A1)(ft) for \(\neg (p \wedge q)\) column correct, (A1) for last column correct.
(ii) Yes. (R1)(ft) (C4)
Note: (ft) from their second and the last columns. Must be correct from their table.[4 marks]
\(p {\underline \vee} q\). (A1)(A1) (C2)
Note: Award (A1) for \(p \ldots q\), (A1) for \({\underline \vee} \). Accept \((p \vee q) \wedge \neg (p \wedge q)\) or \((p \vee q) \wedge (\neg p \vee \neg q)\).[2 marks]
Question
Let \(p\) and \(q\) represent the propositions
\(p\): food may be taken into the cinema
\(q\): drinks may be taken into the cinema
Complete the truth table below for the symbolic statement \(\neg (p \vee q)\) .
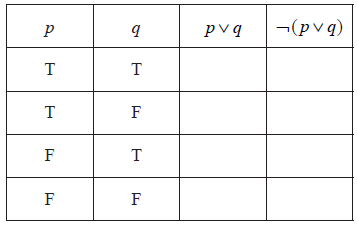[2]
Write down in words the meaning of the symbolic statement \(\neg (p \vee q)\).[2]
Write in symbolic form the compound statement:
“no food and no drinks may be taken into the cinema”.[2]
Answer/Explanation
Markscheme
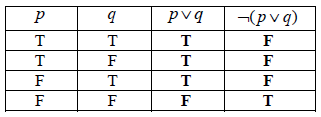(A1)(A1)(ft) (C2)
Note: (A1) for each correct column.[2 marks]
It is not true that food or drinks may be taken into the cinema.
Note: (A1) for “it is not true”. (A1) for “food or drinks”.
OR
Neither food nor drinks may be taken into the cinema.
Note: (A1) for “neither”. (A1) for “nor”.
OR
No food and no drinks may be taken into the cinema.
Note: (A1) for “no food”, “no drinks”. (A1) for “and”.
OR
No food or drink may be brought into the cinema. (A2) (C2)
Note: (A1) for “no”, (A1) for “food or drink”. Do not penalize for use of plural/singular.
Note: the following answers are incorrect:
No food and drink may be brought into the cinema. Award (A1) (A0)
Food and drink may not be brought into the cinema. Award (A1) (A0)
No food or no drink may be brought into the cinema. Award (A1) (A0)[2 marks]
\(\neg p \wedge \neg q\)
Note: (A1) for both negations, (A1) for conjunction.
OR
\(\neg (p \vee q)\) (A1)(A1) (C2)
Note: (A1) for negation, (A1) for \(p \vee q\) in parentheses.[2 marks]
Question
Consider the two propositions p and q.
p: The sun is shining q: I will go swimming
Write in words the compound proposition
\(p \Rightarrow q\) ;[2]
Write in words the compound proposition
\(\neg p \vee q\).[2]
The truth table for these compound propositions is given below.
Complete the column for \( \neg p\).[1]
The truth table for these compound propositions is given below.
State the relationship between the compound propositions \(p \Rightarrow q\) and \(\neg p \vee q\) .[1]
Answer/Explanation
Markscheme
If the sun is shining then I will go swimming. (A1)(A1) (C2)
Note: Award (A1) for “if…then” and (A1) for correct order.[2 marks]
Either the sun is not shining or I will go swimming. (A1)(A1) (C2)
Note: Award (A1) for both correct statements and (A1) for “either” “…or”.[2 marks]
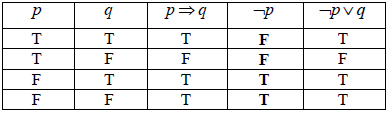(A1) (C1)[1 mark]
They are (logically) equivalent. (A1) (C1)
Note: Do not accept any other answers.[1 mark]
Question
Complete the truth table shown below.
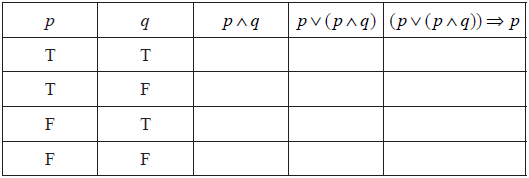
State whether the compound proposition \((p \vee (p \wedge q)) \Rightarrow p\) is a contradiction, a tautology or neither.[1]
Consider the following propositions.
p: Feng finishes his homework
q: Feng goes to the football match
Write in symbolic form the following proposition.
If Feng does not go to the football match then Feng finishes his homework.[2]
Answer/Explanation
Markscheme
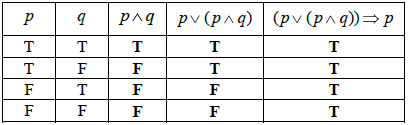(A1)(A1)(ft)(A1)(ft) (C3)
Note: Award (A1) for each correct column.[3 marks]
tautology (A1)(ft) (C1)
Note: Follow through from their last column.[1 mark]
\(\neg q \Rightarrow p\) (A1)(A1) (C2)
Note: Award (A1) for \(\neg q\) and p in correct order, (A1) for \( \Rightarrow \) sign.[2 marks]
Question
Complete the following truth table.
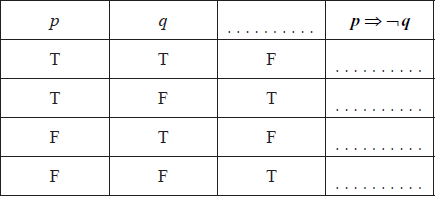[2]
Consider the propositions
p: Cristina understands logic
q: Cristina will do well on the logic test.
Write down the following compound proposition in symbolic form.
“If Cristina understands logic then she will do well on the logic test”[2]
Write down in words the contrapositive of the proposition given in part (b).[2]
Answer/Explanation
Markscheme
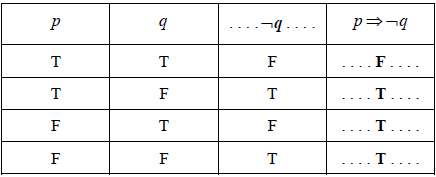(A1)(A1) (C2)
Note: Award (A1) for ¬q , (A1) for last column.[2 marks]
\(p \Rightarrow q\) (A1)(A1) (C2)
Note: Award (A1) for \(\Rightarrow\) , (A1) for p and q in the correct order.[2 marks]
If Cristina does not do well on the logic test then she does not understand logic. (A1)(A1) (C2)
Note: Award (A1) for If…(then), must be an implication, (A1) for the correct propositions in the correct order.[2 marks]
Question
In a particular school, students must choose at least one of three optional subjects: art, psychology or history.
Consider the following propositions
a: I choose art,
p: I choose psychology,
h: I choose history.
Write, in words, the compound proposition
\[\neg h \Rightarrow (p \vee a)\].[3]
Complete the truth table for \(\neg a \Rightarrow p\) .
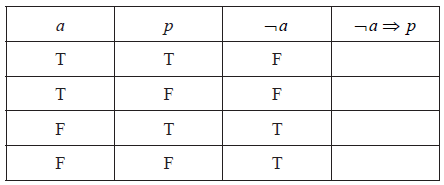[1]
State whether \(\neg a \Rightarrow p\) is a tautology, a contradiction or neither. Justify your answer.[2]
Answer/Explanation
Markscheme
If I do not choose history then I choose either psychology or I choose art (A1)(A1)(A1) (C3)
Notes: Award (A1) for ‘if… (then)…’
Award (A1) for ‘not choose history.’
Award (A1) for ‘choose (either) psychology or art (or both).’
If the order of the statements is wrong award at most (A1)(A1)(A0).[3 marks]
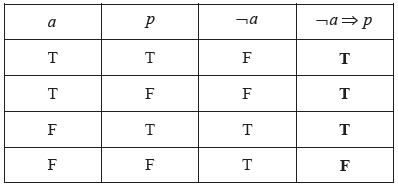(A1) (C1)[1 mark]
Neither, because not all the entries in the last column are the same. (A1)(ft)(R1) (C2)
Notes: Do not award (R0)(A1). Follow through from their answer to part (b). Reasoning must be consistent with their answer to part (b).[2 marks]
Question
Complete the truth table below.
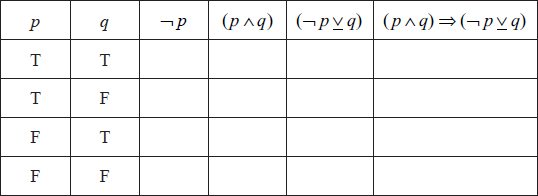[4]
State whether the statement \((p \wedge q) \Rightarrow (\neg p \underline \vee q)\) is a logical contradiction, a tautology or neither.[1]
Give a reason for your answer to part (b)(i).[1]
Answer/Explanation
Markscheme
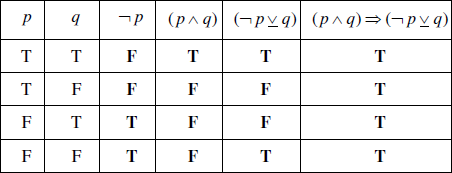(A1)(A1)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1) for each correct column.
Award first (A1)(ft) from their third column in the table.
Award second (A1)(ft) from their fourth and fifth column in the table.[4 marks]
Tautology (A1)(ft) (C1)
Note: Answer must be consistent with last column in table.[1 mark]
All entries (in the final column) are true. (R1)(ft) (C1)
Note: Answer must be consistent with their answer to part (b)(i).
Note: Special case (A1)(R0) may be awarded.[1 mark]
Question
Consider the propositions p and q.
p: I take swimming lessons
q: I can swim 50 metres
Complete the truth table below.
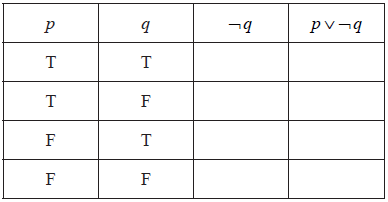[2]
Write the following compound proposition in symbolic form.
“I cannot swim 50 metres and I take swimming lessons.”[2]
Write the following compound proposition in words.
\(q \Rightarrow \neg q \)[2]
Answer/Explanation
Markscheme
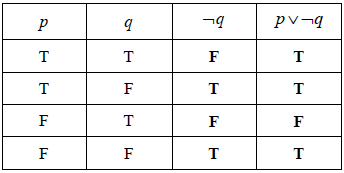(A1)(A1)(ft) (C2)
Notes: Award (A1) for each correct column. Follow through in 4th column from their 3rd column.[2 marks]
\(\neg q \wedge p\) (A1)(A1) (C2)
Note: Award (A1) for \(\neg q\) and p in any order, (A1) for \(\wedge\).[2 marks]
If I can swim 50 metres (then) I do not take swimming lessons. (A1)(A1) (C2)
Note: Award (A1) for If… (then), (A1) for correct propositions in the correct order.[2 marks]
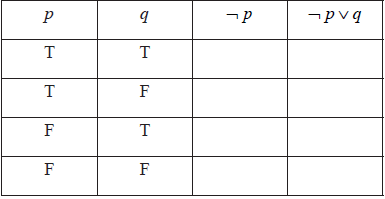
Question
Complete the truth table.
[2]
Consider the propositions p and q:
p: x is a number less than 10.
q: x2 is a number greater than 100.
Write in words the compound proposition \(\neg p \vee q\).[2]
Using part (a), determine whether \(\neg p \vee q\) is true or false, for the case where \(x\) is a number less than 10 and \(x^2\) is a number greater than 100.[1]
Write down a value of \(x\) for which \(\neg p \vee q\) is false.[1]
Answer/Explanation
Markscheme
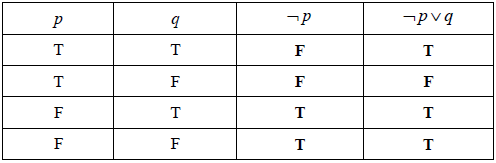
(A1) for third column and (A1)(ft) for fourth column (A1)(A1)(ft) (C2)
\(x\) is greater than or equal to (not less than) 10 or \(x^2\) is greater than 100. (A1)(A1) (C2)
Note: Award (A1) for “greater than or equal to (not less than) 10”, (A1) for “or \(x^2\) is greater than 100”.
True (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
Any value of \(x\) such that \( – 10 \leqslant x < 10\). (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
Question
Consider the following propositions.
p : Students stay up late.
q : Students fall asleep in class.
Write the following compound proposition in symbolic form.
If students do not stay up late then they will not fall asleep in class.[2]
Complete the following truth table.
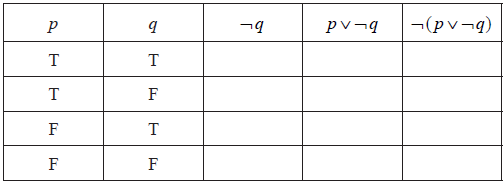[3]
Write down a reason why the statement \(\neg ( p \vee \neg q)\) is not a contradiction.[1]
Answer/Explanation
Markscheme
\(\neg p \Rightarrow \neg q\) (A1)(A1) (C2)
Note: Award (A1) for any 2 correct symbols seen in a statement, (A1) for all 3 correct symbols in correct order.
(A1)(A1)(ft)(A1)(ft) (C3)
Note: Award (A1) for each correct column. 4th column is follow through from 3rd, 5th column is follow through from 4th.
Not all of last column is F (R1)(ft) (C1)
Note: Award (R1)(ft) if final column does not lead to a contradiction.
Question
Consider the propositions
\(p\): I have a bowl of soup.
\(q\): I have an ice cream.
Write down, in words, the compound proposition \(\neg p \Rightarrow q\).[2]
Complete the truth table.
[2]
Write down, in symbolic form, the converse of \(\neg p \Rightarrow q\).[2]
Answer/Explanation
Markscheme
If I do not have a bowl of soup then I have an ice cream. (A1)(A1) (C2)
Notes: Award (A1) for If… then…
Award (A1) for correct statements in correct order.[2 marks]
(A1)(A1)(ft) (C2)
Note: Follow through from third column to fourth column.[2 marks]
\(q \Rightarrow \neg p\) (A1)(A1) (C2)
Notes: Award (A1) for \( \Rightarrow \).
Award (A1) for \(q\) and \(\neg p\) in correct order.
Accept \(\neg p \Leftarrow q\).[2 marks]
Question
Consider the three propositions p, q and r.
p: The food is well cooked
q: The drinks are chilled
r: Dinner is spoilt
Write the following compound proposition in words.
\[(p \wedge q) \Rightarrow \neg r\][3]
Complete the following truth table.
[3]
Answer/Explanation
Markscheme
If the food is well cooked and the drinks are chilled then dinner is not spoilt. (A1)(A1)(A1) (C3)
Note: Award (A1) for “If…then” (then must be seen), (A1) for the two correct propositions connected with “and”, (A1) for “not spoilt”.
Only award the final (A1) if correct statements are given in the correct order.[3 marks]
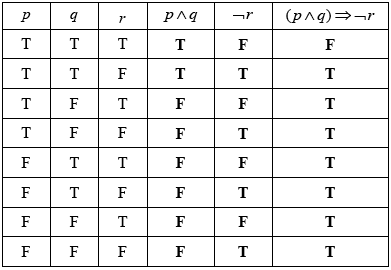(A1)(A1)(A1)(ft) (C3)
Notes: Award (A1) for each correct column.
The final column must follow through from the previous two columns.[3 marks]
Question
Consider the statement \(p \Rightarrow q\).
If I break my arm, then it will hurt.
Write down in words, the inverse of \(p \Rightarrow q\).[2]
Complete the following truth table.
[2]
State whether the converse and the inverse of an implication are logically equivalent.
Justify your answer.[2]
Answer/Explanation
Markscheme
If I do not break my arm, then it will not hurt (A1)(A1) (C2)
Note: Award (A1) for “if… then…”
For Spanish candidates, only accept “Si” and “entonces”.
Award (A1) for “not break my arm” and “not hurt” in correct order.
(A1)(A1) (C2)
Notes: Award (A1) for each correct column.
logically equivalent (A1)(ft)
last two columns of the truth table are identical (R1)(ft) (C2)
Notes: Do not award (A1)(ft)(R0).
Follow through from the last two columns of the table in part (a).
Question
Consider the propositions \(r\), \(p\) and \(q\).
Complete the following truth table.
[4]
Determine whether the compound proposition \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) is a tautology, a contradiction or neither.
Give a reason.[2]
Answer/Explanation
Markscheme
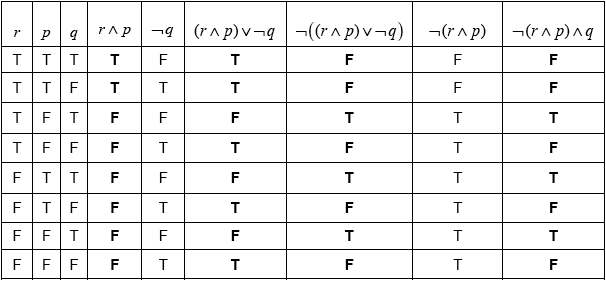(A1)(A1)(ft)(A1)(ft)(A1) (C4)
Notes: Award (A1) for each correct column.
For the “\({(r \wedge p) \vee \neg q}\)” follow through from the “\(r \wedge p\)” column.
For the “\(\neg \left( {(r \wedge p) \vee \neg q)} \right)\)” column, follow through from the preceding column.
tautology (A1)(ft)
columns \(\neg \left( {(r \wedge p) \vee \neg q)} \right)\) and \(\neg (r \wedge p) \wedge q\) are identical (R1)(C2)
Notes: Do not award (R0)(A1)(ft). Follow through from their table in part (a).
Award the (R1) for an additional column representing \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) that is consistent with their table.
Question
Consider the following propositions:
\(p:\) The lesson is cancelled
\(q:\) The teacher is absent
\(r:\) The students are in the library.
Write, in words, the compound proposition \(q \Rightarrow (p \wedge r).\)[3]
Complete the following truth table.
[2]
Hence, justify why \(q \Rightarrow \neg r\) is not a tautology.[1]
Answer/Explanation
Markscheme
if the teacher is absent then the lesson is cancelled and the students are in the library (A1)(A1)(A1) (C3)
Note: Award (A1) for If…then.
For Spanish candidates, only accept “Si” and “entonces”.
For French candidates, only accept “Si” and “alors”.
For all three languages these words are from the subject guide.
Award (A1) for “and”,
Award (A1) for correct propositions in correct order.
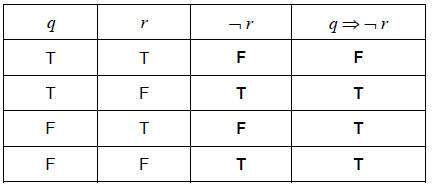
(A1)(A1)(ft) (C2)
Note: Award (A1) for \(\neg r\) column correct and (A1) for \(q \Rightarrow \neg r\) column correct.
Award (A0)(A1)(ft) for a \(q \Rightarrow \neg r\) column that correctly follows from an incorrect \(\neg r\) column.
not all of the entries are true (or equivalent) (R1) (C1)
Note: Accept “One entry is false”.
Question
Consider the following logic propositions.
\(p\): Sandi gets up before eight o’clock
\(q\): Sandi goes for a run
\(r\): Sandi goes for a swim
Write down in words the compound proposition
[3]
Complete the following truth table.
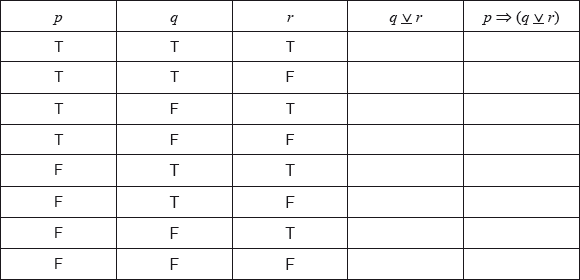[2]
On a morning when Sandi does not get up before eight o’clock, use your truth table to determine whether \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
If Sandi gets up before eight o’clock then Sandi (either) goes for a run or goes for a swim, but not both. (A1)(A1)(A1) (C3)
Note: Award (A1) for If …… then ……, (A1) for all propositions in the correct order, (A1) for “… or … but not both” (do not accept “either” as a replacement for “but not both”).[3 marks]
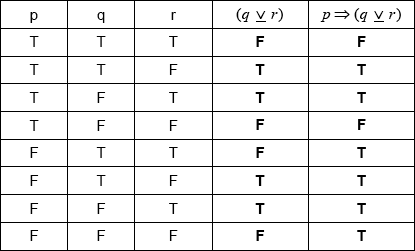(A1)(A1)(ft) (C2)
Note: Award (A1) for correct \((q{\text{ }}\underline \vee {\text{ }}r)\) column, and (A1)(ft) for their correct \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) column. Follow through from their \((q{\text{ }}\underline \vee {\text{ }}r)\) column.[2 marks]
tautology (A1)(ft) (C1)
Note: Follow through from part (b).[1 mark]
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: I completed the task}}} \\ {q{\text{: I was paid}}} \end{array}\]
Write down in words \(\neg q\).[1]
Write down in symbolic form the compound statement:
If I was paid then I completed the task.[1]
Complete the following truth table.
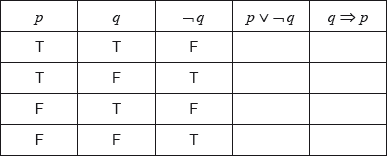[2]
State whether the statements \(p \vee \neg q\) and \(q \Rightarrow p\) are logically equivalent. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
I was not paid (A1) (C1)[1 mark]
\(q \Rightarrow p\) (A1) (C1)[1 mark]
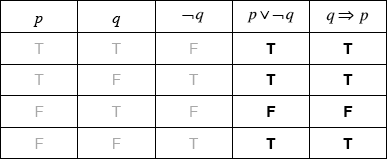(A1)(A1) (C2)
Note: Award (A1) for each correct column.[2 marks]
yes (A1)(ft)
as the last two columns of the truth table are the same (R1)(ft) (C2)
Note: Do not award (A1)(R0). Follow through from part (c)(i).[2 marks]
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: The car is under warranty}}} \\ {q{\text{: The car is less than 2 years old}}} \\ {r{\text{ : The car has been driven more than 20}}\,{\text{000 km}}} \end{array}\]
Write down in words \((q \vee \neg r) \Rightarrow p\).[3]
Complete the truth table.
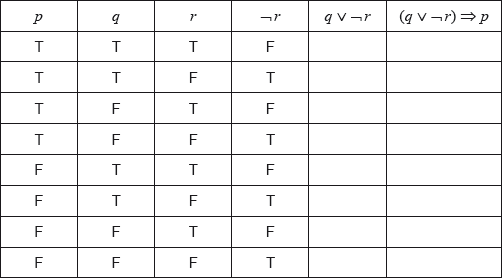[2]
State whether the statement \(\neg p \Rightarrow \neg (q \vee \neg r)\) is the inverse, the converse or the contrapositive of the statement in part (a).[1]
Answer/Explanation
Markscheme
if the car is less than 2 years old or the car has not been driven more than \(20\,000{\text{ km}}\), then the car is under warranty (A1)(A1)(A1) (C3)
Note: Award (A1) for if …, then …, (A1) for “or”, (A1) for correct statements in correct order. Accept “If the car has not been driven more than \(20\,000{\text{ km}}\) or the car is less than 2 years old, then the car is under warranty”. Accept logical equivalent wording for each proposition, eg “less than \(20\,000{\text{ km}}\)”.[3 marks]
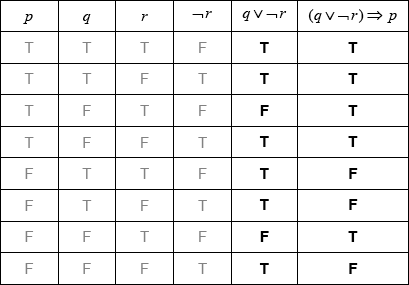(A1)(A1)(ft) (C2)
Note: Award (A1) for \(q \vee \neg r\) column correct and (A1)(ft) for \((q \vee \neg r) \Rightarrow p\) column correct. Follow through from their \(q \vee \neg r\) column.[2 marks]
contrapositive (A1) (C1)[1 mark]
Question
Consider the following propositions.
p: my Mathematical Studies homework is due tomorrow
q: today is Wednesday
Write down in words the compound proposition ¬\(p \Rightarrow q\).[2]
Complete the truth table.
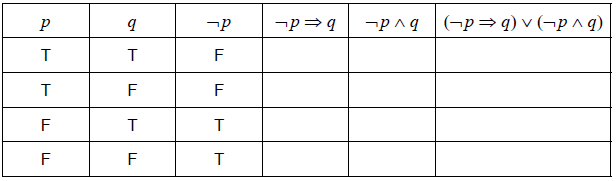[3]
State whether the compound proposition (\(\neg p \Rightarrow q\)) ∨ (\(\neg p \wedge q\)) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
If my Mathematical Studies homework is not due in tomorrow then today is Wednesday. (A1)(A1) (C2)
Note: Award (A1) for If… then…
Award (A1) for correct propositions, my Mathematical Studies homework is not due in tomorrow and today is Wednesday, in the correct order.
Award (A1)(A0) for “If ¬p then q”.[2 marks]
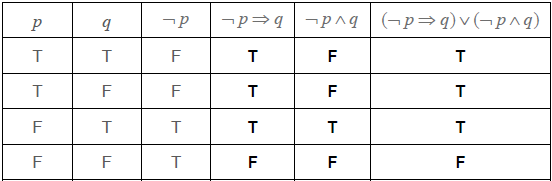(A1)(A1)(A1)(ft) (C3)[3 marks]
neither (A1)(ft) (C1)
Note: Follow through from the final column of their truth table.[1 mark]
Question
Consider the following propositions.
p : the baby cries
q : the baby is happy
r : the baby wants to play
Write down, in words, \(\left( {q \wedge r} \right) \Rightarrow \neg p\).[3]
Complete the following truth table.
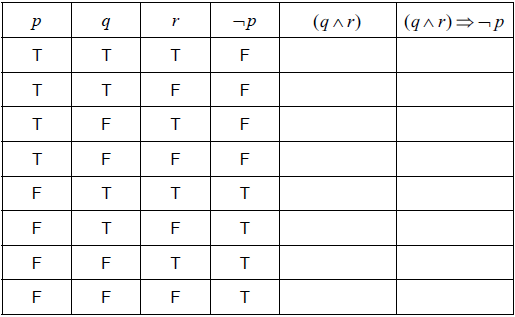[2]
State whether \(\left( {q \wedge r} \right) \Rightarrow \neg p\) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
if the baby is happy and wants to play then the baby does not cry (A1)(A1)(A1) (C3)
Note: Award (A1) for “If… then…”; (A1) for “the baby is happy and wants to play”, (A1) for “the baby does not cry”. Crying must be negated.[3 marks]
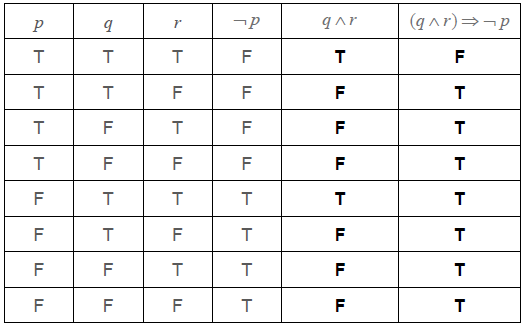(A1)(A1) (C2)
Note: Award (A1) for each correct column.[2 marks]
Neither (A1)(ft) (C1)
Note: Follow through from the last column in their part (b).[1 mark]
Question
Consider each of the following statements
\[p:Alex{\text{ }}is{\text{ }}from{\text{ }}Uruguay\]\[q:Alex{\text{ }}is{\text{ }}a{\text{ }}scientist\]\[r:Alex{\text{ }}plays{\text{ }}the{\text{ }}flute\]
Write the following argument in words
\[\neg r \Rightarrow (q \vee p)\][3]
Complete the truth table for the argument in part (a) using the values below for \(p\) , \(q\) , \(r\) and \(\neg r\).
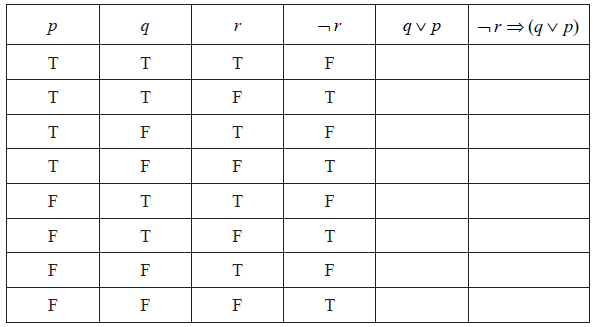[2]
The argument \(\neg r \Rightarrow (q \vee p)\) is invalid. State the reason for this.[1]
Answer/Explanation
Markscheme
If Alex does not play the flute then he is either a scientist or from Uruguay. (A1)(A1)(A1) (C3)
Note: Award (A1) if… then, correct (A1) antecedent, (A1) correct consequent.
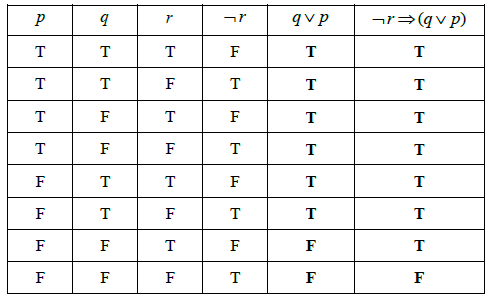(A1)(A1) (C2)
Not all entries in the final column are T. (R1) (C1)