Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
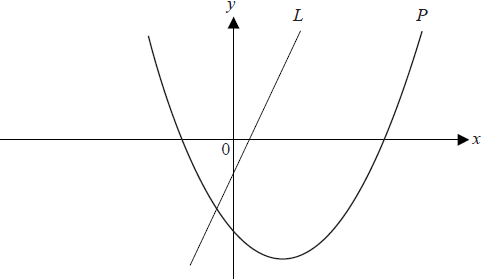
Find the gradient of the line L.[2]
Differentiate \(f (x)\) .[2]
Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
State the equation of the axis of symmetry of P.[1]
Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
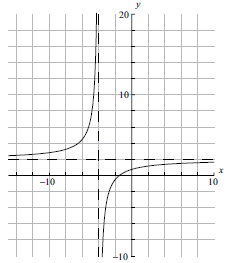
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
Write down the equation of the vertical asymptote.[2]
On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
Answer/Explanation
Markscheme
(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
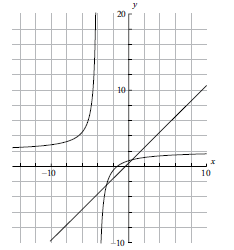(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
On the coordinate axes below, \({\text{D}}\) is a point on the \(y\)-axis and \({\text{E}}\) is a point on the \(x\)-axis. \({\text{O}}\) is the origin. The equation of the line \({\text{DE}}\) is \(y + \frac{1}{2}x = 4\).
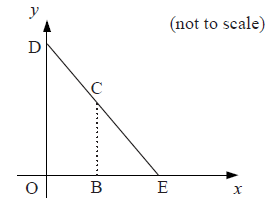
Write down the coordinates of point \({\text{E}}\).[2]
\({\text{C}}\) is a point on the line \({\text{DE}}\). \({\text{B}}\) is a point on the \(x\)-axis such that \({\text{BC}}\) is parallel to the \(y\)-axis. The \(x\)-coordinate of \({\text{C}}\) is \(t\).
Show that the \(y\)-coordinate of \({\text{C}}\) is \(4 – \frac{1}{2}t\).[2]
\({\text{OBCD}}\) is a trapezium. The \(y\)-coordinate of point \({\text{D}}\) is \(4\).
Show that the area of \({\text{OBCD}}\) is \(4t – \frac{1}{4}{t^2}\).[3]
The area of \({\text{OBCD}}\) is \(9.75\) square units. Write down a quadratic equation that expresses this information.[1]
(i) Using your graphic display calculator, or otherwise, find the two solutions to the quadratic equation written in part (d).
(ii) Hence find the correct value for \(t\). Give a reason for your answer.[4]
Answer/Explanation
Markscheme
\({\text{E}}(8{\text{, }}0)\) (A1)(A1)
Notes: Brackets required but do not penalize again if mark lost in Q4 (i)(d). If missing award (A1)(A0).
Accept \(x = 8\), \(y = 0\)
Award (A1) for \(x = 8\)
\(y + \frac{1}{2}t = 4\) (M1)(M1)
Note: (M1) for the equation of the line seen. (M1) for substituting \(t\).
\(y = 4 – \frac{1}{2}t\) (AG)
Note: Final line must be seen or previous (M1) mark is lost.[2 marks]
\({\text{Area}} = \frac{1}{2} \times (4 + 4 – \frac{1}{2}t) \times t\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct substitution.
\( = \frac{1}{2} \times (8 – \frac{1}{2}t) \times t = \frac{1}{2}(8t – \frac{1}{2}{t^2})\) (A1)
\( = 4t – \frac{1}{4}{t^2}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[3 marks]
\(4t – \frac{1}{4}{t^2} = 9.75\) or any equivalent form. (A1)[1 mark]
(i) \(t = 3\) or \(t =13\) (A1)(ft)(A1)(ft)(G2)
Note: Follow through from candidate’s equation to part (d). Award (A0)(A1)(ft) for \((3{\text{, }}0)\) and \((13{\text{, }}0)\).
(ii) \(t\) must be a value between \(0\) and \(8\) then \(t = 3\)
Note: Accept \({\text{B}}\) is between \({\text{O}}\) and \({\text{E}}\). Do not award (R0)(A1).
Question
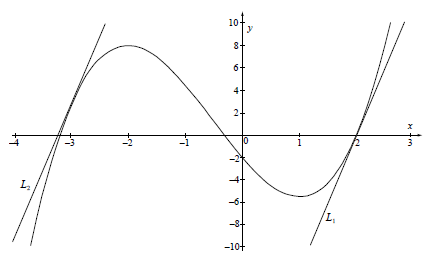
Consider the curve \(y = {x^3} + \frac{3}{2}{x^2} – 6x – 2\) .
(i) Write down the value of \(y\) when \(x\) is \(2\).
(ii) Write down the coordinates of the point where the curve intercepts the \(y\)-axis.[3]
Sketch the curve for \( – 4 \leqslant x \leqslant 3\) and \( – 10 \leqslant y \leqslant 10\). Indicate clearly the information found in (a).[4]
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) .[3]
Let \({L_1}\) be the tangent to the curve at \(x = 2\).
Let \({L_2}\) be a tangent to the curve, parallel to \({L_1}\).
(i) Show that the gradient of \({L_1}\) is \(12\).
(ii) Find the \(x\)-coordinate of the point at which \({L_2}\) and the curve meet.
(iii) Sketch and label \({L_1}\) and \({L_2}\) on the diagram drawn in (b).[8]
It is known that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} > 0\) for \(x < – 2\) and \(x > b\) where \(b\) is positive.
(i) Using your graphic display calculator, or otherwise, find the value of \(b\).
(ii) Describe the behaviour of the curve in the interval \( – 2 < x < b\) .
(iii) Write down the equation of the tangent to the curve at \(x = – 2\).[5]
Answer/Explanation
Markscheme
(i) \(y = 0\) (A1)
(ii) \((0{\text{, }}{- 2})\) (A1)(A1)
Note: Award (A1)(A0) if brackets missing.
OR
\(x = 0{\text{, }}y = – 2\) (A1)(A1)
Note: If coordinates reversed award (A0)(A1)(ft). Two coordinates must be given.[3 marks]
(A4)
Notes: (A1) for appropriate window. Some indication of scale on the \(x\)-axis must be present (for example ticks). Labels not required. (A1) for smooth curve and shape, (A1) for maximum and minimum in approximately correct position, (A1) for \(x\) and \(y\) intercepts found in (a) in approximately correct position.[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 3{x^2} + 3x – 6\) (A1)(A1)(A1)
Note: (A1) for each correct term. Award (A1)(A1)(A0) at most if any other term is present.[3 marks]
(i) \(3 \times 4 + 3 \times 2 – 6 = 12\) (M1)(A1)(AG)
Note: (M1) for using the derivative and substituting \(x = 2\) . (A1) for correct (and clear) substitution. The \(12\) must be seen.
(ii) Gradient of \({L_2}\) is \(12\) (can be implied) (A1)
\(3{x^2} + 3x – 6 = 12\) (M1)
\(x = – 3\) (A1)(G2)
Note: (M1) for equating the derivative to \(12\) or showing a sketch of the derivative together with a line at \(y = 12\) or a table of values showing the \(12\) in the derivative column.
(iii) (A1) for \({L_1}\) correctly drawn at approx the correct point (A1)
(A1) for \({L_2}\) correctly drawn at approx the correct point (A1)
(A1) for 2 parallel lines (A1)
Note: If lines are not labelled award at most (A1)(A1)(A0). Do not accept 2 horizontal or 2 vertical parallel lines.[8 marks]
(i) \(b = 1\) (G2)
(ii) The curve is decreasing. (A1)
Note: Accept any valid description.
(iii) \(y = 8\) (A1)(A1)(G2)
Note: (A1) for “\(y =\) a constant”, (A1) for \(8\).[5 marks]
Question
The vertices of quadrilateral ABCD as shown in the diagram are A (3, 1), B (0, 2), C (–2, 1) and D (–1, –1).
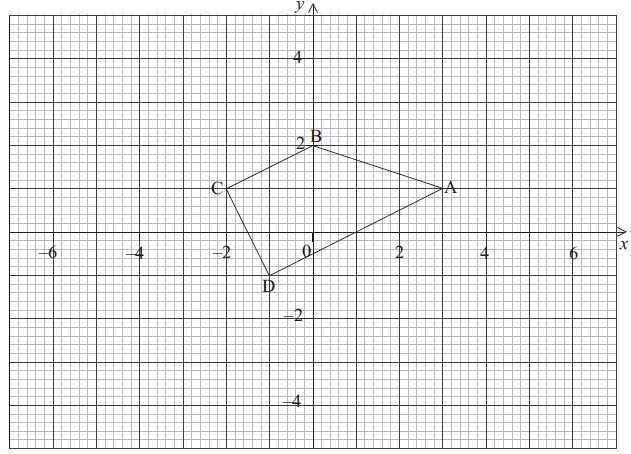
Calculate the gradient of line CD.[2]
Show that line AD is perpendicular to line CD.[2]
Find the equation of line CD. Give your answer in the form \(ax + by = c\) where \(a,{\text{ }}b,{\text{ }}c \in \mathbb{Z}\).[3]
Lines AB and CD intersect at point E. The equation of line AB is \(x + 3y = 6\).
Find the coordinates of E.[2]
Lines AB and CD intersect at point E. The equation of line AB is \(x + 3y = 6\).
Find the distance between A and D.[2]
The distance between D and E is \(\sqrt{20}\).
Find the area of triangle ADE.[2]
Answer/Explanation
Markscheme
\({\text{Gradient of CD}} = \frac{{1 – ( – 1)}}{{ – 2 – ( – 1)}}\) (M1)
\( = – 2\) (A1)(G2)
Note: Award (M1) for correct substitution in gradient formula.[2 marks]
\({\text{Gradient of AD}} = \frac{1}{2}\) (A1)
\( – 2 \times \frac{1}{2} = – 1\) or \(\frac{1}{2}\) is negative reciprocal of –2 (M1)
Hence AD is perpendicular for CD. (AG)
Note: Last line must be seen for the (M1) to be awarded.[2 marks]
\(y = -2x – 3\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for their (a), (A1)(ft) for –3.
If part (a) incorrect award (A1)(ft) for their y-intercept only if working is seen.
OR
\(y – 1 = -2(x + 2)\) (A1)(ft)(A1)
OR
\(y + 1 = -2(x + 1)\) (A1)(ft)(A1)
Note: Award (A1)(ft) for their (a), (A1) for correct substitution of point.
\(2x + y = -3\) (A1)(ft)
Note: The final (A1)(ft) is for their equation in the stated form.[3 marks]
E (−3, 3) (Accept x = −3, y = 3) (G2)
OR
Award (M1) for solving the pair of simultaneous equations by hand. (A1)(ft) for correct answer, (ft) from their (c). (M1)(A1)(ft)
OR
Award (M1) for having extended the lines in their own graph seen drawn on answer paper. (A1) for correct answer. (M1)(A1)
Note: Missing coordinate brackets receive (G1)(G0) or (M1)(A0).[2 marks]
Distance between A and D = \(\sqrt {4^2 + 2^2}\) (M1)
\( = \sqrt{20}\) OR \(2 \sqrt {5}\) OR 4.47 (3 s.f.) (A1)(G2)
Note: Award (M1) for correct substitution into the distance formula, (A1) for correct answer.[2 marks]
Area of ADE = \(\frac{1}{2}\sqrt {20} \times \sqrt {20} \) (M1)
= 10 (A1)(ft)(G2)
Follow through from (e).[2 marks]
Question
The diagram shows triangle ABC. Point C has coordinates (4, 7) and the equation of the line AB is x + 2y = 8.
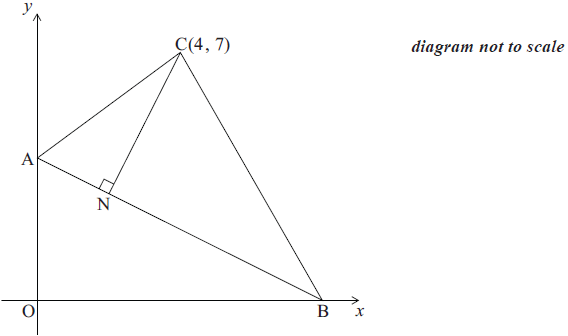
Find the coordinates of A.[1]
Find the coordinates of B.[1]
Show that the distance between A and B is 8.94 correct to 3 significant figures.[2]
N lies on the line AB. The line CN is perpendicular to the line AB.
Find the gradient of CN.[3]
N lies on the line AB. The line CN is perpendicular to the line AB.
Find the equation of CN.[2]
N lies on the line AB. The line CN is perpendicular to the line AB.
Calculate the coordinates of N.[3]
It is known that AC = 5 and BC = 8.06.
Calculate the size of angle ACB.[3]
It is known that AC = 5 and BC = 8.06.
Calculate the area of triangle ACB.[3]
Answer/Explanation
Markscheme
A(0, 4) Accept x = 0, y = 4 (A1)[1 mark]
B(8, 0) Accept x = 8, y = 0 (A1)(ft)
Note: Award (A0) if coordinates are reversed in (i) and (A1)(ft) in (ii).[1 mark]
\({\text{AB}} = \sqrt {{8^2} + {4^2}} {\text{ }} = \sqrt {80} \) (M1)
AB = 8.944 (A1)
= 8.94 (AG)[2 marks]
y = –0.5x + 4 (M1)
Gradient AB = –0.5 (A1)
Note: Award (A2) if –0.5 seen.
OR
Gradient \({\text{AB}} = \frac{{(0 – 4)}}{{(8 – 0)}}\) (M1)
\( = -\frac{1}{2}\) (A1)
Note: Award (M1) for correct substitution in the gradient formula. Follow through from their answers to part (a).
Gradient CN = 2 (A1)(ft)(G2)
Note: Special case: Follow through for gradient CN from their gradient AB.[3 marks]
CN: y = 2x + c
7 = 2(4) + c (M1)
Note: Award (M1)for correct substitution in equation of a line.
y = 2x – 1 (A1)(ft)(G2)
Note: Accept alternative forms for the equation of a line including y – 7 = 2(x – 4) . Follow through from their gradient in (i).
Note: If c = –1 seen but final answer is not given, award (A1)(d).[2 marks]
x + 2(2x – 1) = 8 or equivalent (M1)
N(2, 3) (x = 2, y = 3) (A1)(A1)(ft)(G3)
Note: Award (M1) for attempt to solve simultaneous equations or a sketch of the two lines with an indication of the point of intersection.[3 marks]
Cosine rule: \(\cos ({\rm{A\hat CB)}} = \frac{{{5^2} + {{8.06}^2} – {{8.944}^2}}}{{2 \times 5 \times 8.06}}\) (M1)(A1)
Note: Award (M1) for use of cosine rule with numbers from the problem substituted, (A1) for correct substitution.
\({\rm{A\hat CB = 82.9^\circ }}\) (A1)(G2)
Note: If alternative right-angled trigonometry method used award (M1) for use of trig ratio in both triangles, (A1) for correct substitution of their values in each ratio, (A1) for answer.
Note: Accept 82.8° with use of 8.94.[3 marks]
Area \({\text{ACB}} = \frac{{5 \times 8.06\sin (82.9)}}{2}\) (M1)(A1)(ft)
Note: Award (M1) for substituted area formula, (A1) for correct substitution. Follow through from their angle in part (e).
OR
Area \({\text{ACB}} = \frac{{{\text{AB}} \times {\text{CN}}}}{2} = \frac{{8.94 \times \sqrt {{{(4 – 2)}^2} + {{(7 – 3)}^2}} }}{2}\) (M1)(M1)(ft)
Note: Award (M1) substituted area formula with their values, (M1) for substituted distance formula. Follow through from
coordinates of N.
Area ACB = 20.0 (A1)(ft)(G2)
Note: Accept 20[3 marks]
Question
The diagram shows a sketch of the function f (x) = 4x3 − 9x2 − 12x + 3.
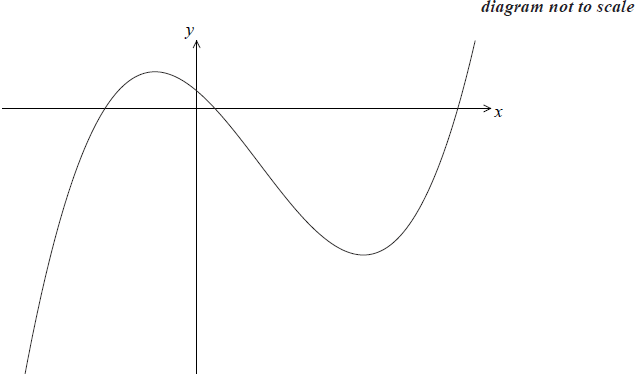
Write down the values of x where the graph of f (x) intersects the x-axis.[3]
Write down f ′(x).[3]
Find the value of the local maximum of y = f (x).[4]
Let P be the point where the graph of f (x) intersects the y axis.
Write down the coordinates of P.[1]
Let P be the point where the graph of f (x) intersects the y axis.
Find the gradient of the curve at P.[2]
The line, L, is the tangent to the graph of f (x) at P.
Find the equation of L in the form y = mx + c.[2]
There is a second point, Q, on the curve at which the tangent to f (x) is parallel to L.
Write down the gradient of the tangent at Q.[1]
There is a second point, Q, on the curve at which the tangent to f (x) is parallel to L.
Calculate the x-coordinate of Q.[3]
Answer/Explanation
Markscheme
–1.10, 0.218, 3.13 (A1)(A1)(A1)[3 marks]
f ′(x) = 12x2 – 18x – 12 (A1)(A1)(A1)
Note: Award (A1) for each correct term and award maximum of (A1)(A1) if other terms seen.[3 marks]
f ′(x) = 0 (M1)
x = –0.5, 2
x = –0.5 (A1)
Note: If x = –0.5 not stated, can be inferred from working below.
y = 4(–0.5)3 – 9(–0.5)2 – 12(–0.5) + 3 (M1)
y = 6.25 (A1)(G3)
Note: Award (M1) for their value of x substituted into f (x).
Award (M1)(G2) if sketch shown as method. If coordinate pair given then award (M1)(A1)(M1)(A0). If coordinate pair given with no working award (G2).[4 marks]
(0, 3) (A1)
Note: Accept x = 0, y = 3.[1 mark]
f ′(0) = –12 (M1)(A1)(ft)(G2)
Note: Award (M1) for substituting x = 0 into their derivative.[2 marks]
Tangent: y = –12x + 3 (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for their gradient, (A1) for intercept = 3.
Award (A1)(A0) if y = not seen.[2 marks]
–12 (A1)(ft)
Note: Follow through from their part (e).[1 mark]
12x2 – 18x – 12 = –12 (M1)
12x2 – 18x = 0 (M1)
x = 1.5, 0
At Q x = 1.5 (A1)(ft)(G2)
Note: Award (M1)(G2) for 12x2 – 18x – 12 = –12 followed by x = 1.5.
Follow through from their part (g).[3 marks]
Question
The points A (−4, 1), B (0, 9) and C (4, 2) are plotted on the diagram below. The diagram also shows the lines AB, L1 and L2.
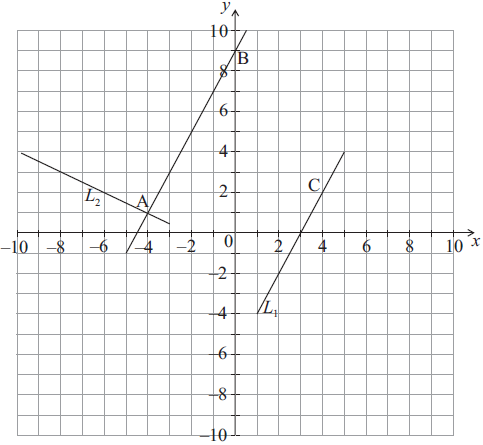
Find the gradient of AB.[2]
L1 passes through C and is parallel to AB.
Write down the y-intercept of L1.[1]
L2 passes through A and is perpendicular to AB.
Write down the equation of L2. Give your answer in the form ax + by + d = 0 where a, b and d \( \in \mathbb{Z}\).[3]
Write down the coordinates of the point D, the intersection of L1 and L2.[1]
There is a point R on L1 such that ABRD is a rectangle.
Write down the coordinates of R.[2]
The distance between A and D is \(\sqrt {45} \).
(i) Find the distance between D and R .
(ii) Find the area of the triangle BDR .[4]
Answer/Explanation
Markscheme
\(\frac{{9 – 1}}{{0 – ( – 4)}}\) (M1)
= 2 (A1)(G2)
Notes: Award (M1) for correct substitution into the gradient formula.[2 marks]
–6 (A1)
Note: Accept (0, –6) .[1 mark]
\(y = – \frac{1}{2}x – 1\) (or equivalent) (A1)(ft)(A1)
Notes: Award (A1)(ft) for gradient, (A1) for correct y-intercept. Follow through from their gradient in (a).
x + 2y + 2 = 0 (A1)(ft)
Notes: Award (A1)(ft) from their gradient and their y-intercept. Accept any multiple of this equation with integer coefficients.
OR
\(y – 1 = – \frac{1}{2}(x + 4)\) (or equivalent) (A1)(ft)(A1)
Note: Award (A1)(ft) for gradient, (A1) for any point on the line correctly substituted in equation.
x + 2y + 2 = 0 (A1)(ft)
Notes: Award (A1)(ft) from their equation. Accept any multiple of this equation with integer coefficients.[3 marks]
D(2, –2) or x = 2, y = –2 (A1)
Note: Award (A0) if brackets not present.[1 mark]
R(6, 6) or x = 6, y = 6 (A1)(A1)
Note: Award at most (A0)(A1)(ft) if brackets not present and absence of brackets has not already been penalised in part (d).[2 marks]
(i) \({\text{DR}} = \sqrt {{8^2} + {4^2}} \) (M1)
\({\text{DR}} = \sqrt {80} \) (8.94) (A1)(ft)(G2)
Note: Award (M1) for correct substitution into the distance formula. Follow through from their D and R.
(ii) \({\text{Area}} = \frac{{\sqrt {80} \times \sqrt {45} }}{2}\) (M1)
= 30 (30.0) (A1)(ft)(G2)
Note: Award (M1) for correct substitution in the area of triangle formula. Follow through from their answer to part (f) (i).[4 marks]
Question
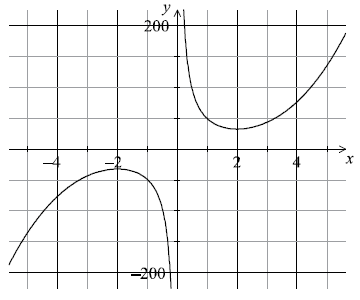
Consider the function \(f(x) = {x^3} + \frac{{48}}{x}{\text{, }}x \ne 0\).
Calculate \(f(2)\) .[2]
Sketch the graph of the function \(y = f(x)\) for \( – 5 \leqslant x \leqslant 5\) and \( – 200 \leqslant y \leqslant 200\) .[4]
Find \(f'(x)\) .[3]
Find \(f'(2)\) .[2]
Write down the coordinates of the local maximum point on the graph of \(f\) .[2]
Find the gradient of the tangent to the graph of \(f\) at \(x = 1\).[2]
There is a second point on the graph of \(f\) at which the tangent is parallel to the tangent at \(x = 1\).
Find the \(x\)-coordinate of this point.[2]
Answer/Explanation
Markscheme
\(f(2) = {2^3} + \frac{{48}}{2}\) (M1)
\(= 32\) (A1)(G2)[2 marks]
(A1) for labels and some indication of scale in an appropriate window
(A1) for correct shape of the two unconnected and smooth branches
(A1) for maximum and minimum in approximately correct positions
(A1) for asymptotic behaviour at \(y\)-axis (A4)
Notes: Please be rigorous.
The axes need not be drawn with a ruler.
The branches must be smooth: a single continuous line that does not deviate from its proper direction.
The position of the maximum and minimum points must be symmetrical about the origin.
The \(y\)-axis must be an asymptote for both branches. Neither branch should touch the axis nor must the curve approach the
asymptote then deviate away later.[4 marks]
\(f'(x) = 3{x^2} – \frac{{48}}{{{x^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(3{x^2}\) , (A1) for \( – 48\) , (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A0) if extra terms seen.[3 marks]
\(f'(2) = 3{(2)^2} – \frac{{48}}{{{{(2)}^2}}}\) (M1)
Note: Award (M1) for substitution of \(x = 2\) into their derivative.
\(= 0\) (A1)(ft)(G1)[2 marks]
\(( – 2{\text{, }} – 32)\) or \(x = – 2\), \(y = – 32\) (G1)(G1)
Notes: Award (G0)(G0) for \(x = – 32\), \(y = – 2\) . Award at most (G0)(G1) if parentheses are omitted.[2 marks]
\(\{ y \geqslant 32\} \cup \{ y \leqslant – 32\} \) (A1)(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) \(y \geqslant 32\) or \(y > 32\) seen, (A1)(ft) for \(y \leqslant – 32\) or \(y < – 32\) , (A1) for weak (non-strict) inequalities used in both of the above.
Accept use of \(f\) in place of \(y\). Accept alternative interval notation.
Follow through from their (a) and (e).
If domain is given award (A0)(A0)(A0).
Award (A0)(A1)(ft)(A1)(ft) for \([ – 200{\text{, }} – 32]\) , \([32{\text{, }}200]\).
Award (A0)(A1)(ft)(A1)(ft) for \(] – 200{\text{, }} – 32]\) , \([32{\text{, }}200[\).[3 marks]
\(f'(1) = – 45\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for \(f'(1)\) seen or substitution of \(x = 1\) into their derivative. Follow through from their derivative if working is seen.[2 marks]
\(x = – 1\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for equating their derivative to their \( – 45\) or for seeing parallel lines on their graph in the approximately correct position.[2 marks]
Question
The diagram shows part of the graph of \(f(x) = {x^2} – 2x + \frac{9}{x}\) , where \(x \ne 0\) .
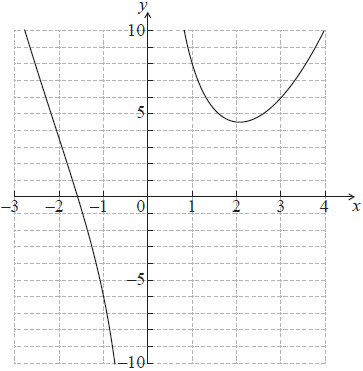
Write down
(i) the equation of the vertical asymptote to the graph of \(y = f (x)\) ;
(ii) the solution to the equation \(f (x) = 0\) ;
(iii) the coordinates of the local minimum point.[5]
Find \(f'(x)\) .[4]
Show that \(f'(x)\) can be written as \(f'(x) = \frac{{2{x^3} – 2{x^2} – 9}}{{{x^2}}}\) .[2]
Find the gradient of the tangent to \(y = f (x)\) at the point \({\text{A}}(1{\text{, }}8)\) .[2]
The line, \(L\), passes through the point A and is perpendicular to the tangent at A.
Write down the gradient of \(L\) .[1]
The line, \(L\) , passes through the point A and is perpendicular to the tangent at A.
Find the equation of \(L\) . Give your answer in the form \(y = mx + c\) .[3]
The line, \(L\) , passes through the point A and is perpendicular to the tangent at A.
\(L\) also intersects the graph of \(y = f (x)\) at points B and C . Write down the x-coordinate of B and of C .[2]
Answer/Explanation
Markscheme
(i) \(x = 0\) (A1)(A1)
Note: Award (A1) for \(x = \) a constant, (A1) for the constant in their equation being \(0\).
(ii) \( – 1.58\) (\( – 1.58454 \ldots \)) (G1)
Note: Accept \( – 1.6\), do not accept \( – 2\) or \( – 1.59\).
(iii) \((2.06{\text{, }}4.49)\) \((2.06020 \ldots {\text{, }}4.49253 \ldots )\) (G1)(G1)
Note: Award at most (G1)(G0) if brackets not used. Award (G0)(G1)(ft) if coordinates are reversed.
Note: Accept \(x = 2.06\), \(y = 4.49\) .
Note: Accept \(2.1\), do not accept \(2.0\) or \(2\). Accept \(4.5\), do not accept \(5\) or \(4.50\).[5 marks]
\(f'(x) = 2x – 2 – \frac{9}{{{x^2}}}\) (A1)(A1)(A1)(A1)
Notes: Award (A1) for \(2x\), (A1) for \( – 2\), (A1) for \( – 9\), (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A1)(A0) if there are extra terms present.[4 marks]
\(f'(x) = \frac{{{x^2}(2x – 2)}}{{{x^2}}} – \frac{9}{{{x^2}}}\) (M1)
Note: Award (M1) for taking the correct common denominator.
\( = \frac{{(2{x^3} – 2{x^2})}}{{{x^2}}} – \frac{9}{{{x^2}}}\) (M1)
Note: Award (M1) for multiplying brackets or equivalent.
\( = \frac{{2{x^3} – 2{x^2} – 9}}{{{x^2}}}\) (AG)
Note: The final (M1) is not awarded if the given answer is not seen.[2 marks]
\(f'(1) = \frac{{2{{(1)}^3} – 2(1) – 9}}{{{{(1)}^2}}}\) (M1)
\( = – 9\) (A1)(G2)
Note: Award (M1) for substitution into given (or their correct) \(f'(x)\) . There is no follow through for use of their incorrect derivative.[2 marks]
\(\frac{1}{9}\) (A1)(ft)
Note: Follow through from part (d).[1 mark]
\(y – 8 = \frac{1}{9}(x – 1)\) (M1)(M1)
Notes: Award (M1) for substitution of their gradient from (e), (M1) for substitution of given point. Accept all forms of straight line.
\(y = \frac{1}{9}x + \frac{{71}}{9}\) (\(y = 0.111111 \ldots x + 7.88888 \ldots \)) (A1)(ft)(G3)
Note: Award the final (A1)(ft) for a correctly rearranged formula of their straight line in (f). Accept \(0.11x\), do not accept \(0.1x\). Accept \(7.9\), do not accept \(7.88\), do not accept \(7.8\).[3 marks]
\( – 2.50\), \(3.61\) (\( – 2.49545 \ldots \), \(3.60656 \ldots \)) (A1)(ft)(A1)(ft)
Notes: Follow through from their line \(L\) from part (f) even if no working shown. Award at most (A0)(A1)(ft) if their correct coordinate pairs given.
Note: Accept \( – 2.5\), do not accept \( – 2.49\). Accept \(3.6\), do not accept \(3.60\).[2 marks]
Question
The graph of the function \(f(x) = \frac{{14}}{x} + x – 6\), for 1 ≤ x ≤ 7 is given below.
Calculate \(f (1)\).[2]
Find \(f ′(x)\).[3]
Use your answer to part (b) to show that the x-coordinate of the local minimum point of the graph of \(f\) is 3.7 correct to 2 significant figures.[3]
Find the range of \(f\).[3]
Points A and B lie on the graph of \(f\). The x-coordinates of A and B are 1 and 7 respectively.
Write down the y-coordinate of B.[1]
Points A and B lie on the graph of f . The x-coordinates of A and B are 1 and 7 respectively.
Find the gradient of the straight line passing through A and B.[2]
M is the midpoint of the line segment AB.
Write down the coordinates of M.[2]
L is the tangent to the graph of the function \(y = f (x)\), at the point on the graph with the same x-coordinate as M.
Find the gradient of L.[2]
Find the equation of L. Give your answer in the form \(y = mx + c\).[3]
Answer/Explanation
Markscheme
\(\frac{{14}}{{(1)}} + (1) – 6\) (M1)
Note: Award (M1) for substituting \(x = 1\) into \(f\).
\(= 9\) (A1)(G2)
\( – \frac{{14}}{{{x^2}}} + 1\) (A3)
Note: Award (A1) for \(-14\), (A1) for \(\frac{{14}}{{{x^2}}}\) or for \(x^{-2}\), (A1) for \(1\).
Award at most (A2) if any extra terms are present.
\( – \frac{{14}}{{{x^2}}} + 1 = 0\) or \(f ‘ (x) = 0 \) (M1)
Note: Award (M1) for equating their derivative in part (b) to 0.
\(\frac{{14}}{{{x^2}}} = 1\) or \({x^2} = 14\) or equivalent (M1)
Note: Award (M1) for correct rearrangement of their equation.
\(x = 3.74165…(\sqrt {14})\) (A1)
\(x = 3.7\) (AG)
Notes: Both the unrounded and rounded answers must be seen to award the (A1). This is a “show that” question; appeals to their GDC are not accepted –award a maximum of (M1)(M0)(A0).
Specifically, \( – \frac{{14}}{{{x^2}}} + 1 = 0\) followed by \(x = 3.74165…, x = 3.7\) is awarded (M1)(M0)(A0).
\(1.48 \leqslant y \leqslant 9\) (A1)(A1)(ft)(A1)
Note: Accept alternative notations, for example [1.48,9]. (\(x = \sqrt{14}\) leads to answer 1.48331…)
Note: Award (A1) for 1.48331…seen, accept 1.48378… from using the given answer \(x = 3.7\), (A1)(ft) for their 9 from part (a) seen, (A1) for the correct notation for their interval (accept \( \leqslant y \leqslant \) or \( \leqslant f \leqslant \) ).
3 (A1)
Note: Do not accept a coordinate pair.
\(\frac{{3 – 9}}{{7 – 1}}\) (M1)
Note: Award (M1) for their correct substitution into the gradient formula.
\(= -1\) (A1)(ft)(G2)
Note: Follow through from their answers to parts (a) and (e).
(4, 6) (A1)(ft)(A1)
Note: Accept \(x = 4\), \(y = 6\). Award at most (A1)(A0) if parentheses not seen.
If coordinates reversed award (A0)(A1)(ft).
Follow through from their answers to parts (a) and (e).
\( – \frac{{14}}{{{4^2}}} + 1\) (M1)
Note: Award (M1) for substitution into their gradient function.
Follow through from their answers to parts (b) and (g).
\( = \frac{1}{8}(0.125)\) (A1)(ft)(G2)
\(y – 1.5 = \frac{1}{8}(x – 4)\) (M1)(ft)(M1)
Note: Award (M1) for substituting their (4, 1.5) in any straight line formula,
(M1) for substituting their gradient in any straight line formula.
\(y = \frac{x}{8} + 4\) (A1)(ft)(G2)
Note: The form of the line has been specified in the question.
Question
The diagram shows an aerial view of a bicycle track. The track can be modelled by the quadratic function
\(y = \frac{{ – {x^2}}}{{10}} + \frac{{27}}{2}x\), where \(x \geqslant 0,{\text{ }}y \geqslant 0\)
(x , y) are the coordinates of a point x metres east and y metres north of O , where O is the origin (0, 0) . B is a point on the bicycle track with coordinates (100, 350)
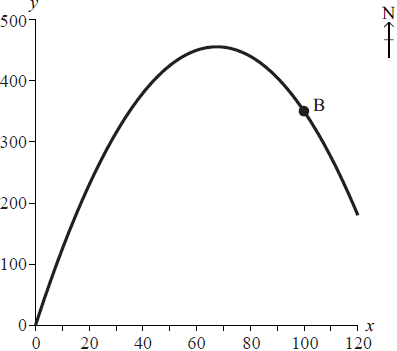
The coordinates of point A are (75, 450). Determine whether point A is on the bicycle track. Give a reason for your answer.[3]
Find the derivative of \(y = \frac{{ – {x^2}}}{{10}} + \frac{{27}}{2}x\).[2]
Use the answer in part (b) to determine if A (75, 450) is the point furthest north on the track between O and B. Give a reason for your answer.[4]
(i) Write down the midpoint of the line segment OB.
(ii) Find the gradient of the line segment OB.[3]
Scott starts from a point C(0,150) . He hikes along a straight road towards the bicycle track, parallel to the line segment OB.
Find the equation of Scott’s road. Express your answer in the form \(ax + by = c\), where \(a, b {\text{ and }} c \in \mathbb{R}\).[3]
Use your graphic display calculator to find the coordinates of the point where Scott first crosses the bicycle track.[2]
Answer/Explanation
Markscheme
\(y = – \frac{{{{75}^2}}}{{10}} + \frac{{27}}{2} \times 75\) (M1)
Note: Award (M1) for substitution of 75 in the formula of the function.
= 450 (A1)
Yes, point A is on the bike track. (A1)
Note: Do not award the final (A1) if correct working is not seen.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2x}}{{10}} + \frac{{27}}{2}\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.2x + 13.5} \right)\) (A1)(A1)
Notes: Award (A1) for each correct term. If extra terms are seen award at most (A1)(A0). Accept equivalent forms.
\( – \frac{{2x}}{{10}} + \frac{{27}}{2} = 0\) (M1)
Note: Award (M1) for equating their derivative from part (b) to zero.
\(x = 67.5\) (A1)(ft)
Note: Follow through from their derivative from part (b).
\( {\text{(Their) }} 67.5 \ne 75\) (R1)
Note: Award (R1) for a comparison of their 67.5 with 75. Comparison may be implied (eg 67.5 is the x-coordinate of the furthest north point).
OR
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2 \times (75)}}{{10}} + \frac{{27}}{2}\) (M1)
Note: Award (M1) for substitution of 75 into their derivative from part (b).
\(= -1.5\) (A1)(ft)
Note: Follow through from their derivative from part (b).
\({\text{(Their)}} -1.5 \ne 0\) (R1)
Note: Award (R1) for a comparison of their –1.5 with 0. Comparison may be implied (eg The gradient of the parabola at the furthest north point (vertex) is 0).
Hence A is not the furthest north point. (A1)(ft)
Note: Do not award (R0)(A1)(ft). Follow through from their derivative from part (b).
(i) M(50,175) (A1)
Note: If parentheses are omitted award (A0). Accept x = 50, y = 175.
(ii) \(\frac{{350 – 0}}{{100 – 0}}\) (M1)
Note: Award (M1) for correct substitution in gradient formula.
\( = 3.5\left( {\frac{{350}}{{100}},\frac{7}{2}} \right)\) (A1)(ft)(G2)
Note: Follow through from (d)(i) if midpoint is used to calculate gradient. Award (G1)(G0) for answer 3.5x without working.
\(y = 3.5x + 150\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for using their gradient from part (d), (A1)(ft) for correct equation of line.
\(3.5x – y = -150\) or \(7x – 2y = -300\) (or equivalent) (A1)(ft)
Note: Award (A1)(ft) for expressing their equation in the form \(ax + by = c\).
(18.4, 214) (18.3772…, 214.320…) (A1)(ft)(A1)(ft)(G2)(ft)
Notes: Follow through from their equation in (e). Coordinates must be positive for follow through marks to be awarded. If parentheses are omitted and not already penalized in (d)(i) award at most (A0)(A1)(ft). If coordinates of the two intersection points are given award (A0)(A1)(ft). Accept x = 18.4, y = 214.
Question
Consider the function \(f(x) = \frac{3}{4}{x^4} – {x^3} – 9{x^2} + 20\).
Find \(f( – 2)\).[2]
Find \(f'(x)\).[3]
The graph of the function \(f(x)\) has a local minimum at the point where \(x = – 2\).
Using your answer to part (b), show that there is a second local minimum at \(x = 3\).[5]
The graph of the function \(f(x)\) has a local minimum at the point where \(x = – 2\).
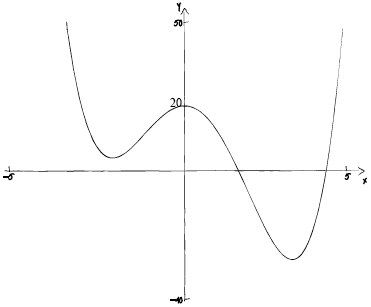
Sketch the graph of the function \(f(x)\) for \( – 5 \leqslant x \leqslant 5\) and \( – 40 \leqslant y \leqslant 50\). Indicate on your
sketch the coordinates of the \(y\)-intercept.[4]
The graph of the function \(f(x)\) has a local minimum at the point where \(x = – 2\).
Write down the coordinates of the local maximum.[2]
Let \(T\) be the tangent to the graph of the function \(f(x)\) at the point \((2, –12)\).
Find the gradient of \(T\).[2]
The line \(L\) passes through the point \((2, −12)\) and is perpendicular to \(T\).
\(L\) has equation \(x + by + c = 0\), where \(b\) and \(c \in \mathbb{Z}\).
Find
(i) the gradient of \(L\);
(ii) the value of \(b\) and the value of \(c\).[5]
Answer/Explanation
Markscheme
\(\frac{3}{4}{( – 2)^4} – {( – 2)^3} – 9{( – 2)^2} + 20\) (M1)
Note: Award (M1) for substituting \(x = – 2\) in the function.
\(= 4\) (A1)(G2)
Note: If the coordinates \(( – 2,{\text{ }}4)\) are given as the answer award, at most, (M1)(A0). If no working shown award (G1).
If \(x = – 2,{\text{ }}y = 4\) seen then award full marks.[2 marks]
\(3{x^3} – 3{x^2} – 18x\) (A1)(A1)(A1)
Note: Award (A1) for each correct term, award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
\(f'(3) = 3 \times {(3)^3} – 3 \times {(3)^2} – 18 \times 3\) (M1)
Note: Award (M1) for substitution in their \(f'(x)\) of \(x = 3\).
\( = 0\) (A1)
OR
\(3{x^3} – 3{x^2} – 18x = 0\) (M1)
Note: Award (M1) for equating their \(f'(x)\) to zero.
\(x = 3\) (A1)
\(f'({x_1}) = 3 \times {({x_1})^3} – 3 \times {({x_1})^2} – 18 \times {x_1} < 0\) where \(0 < {x_1} < 3\) (M1)
Note: Award (M1) for substituting a value of \({x_1}\) in the range \(0 < {x_1} < 3\) into their \(f’\) and showing it is negative (decreasing).
\(f'({x_2}) = 3 \times {({x_2})^3} – 3 \times {({x_2})^2} – 18 \times {x_2} > 0\) where \({x_2} > 3\) (M1)
Note: Award (M1) for substituting a value of \({x_2}\) in the range \({x_2} > 3\) into their \(f’\) and showing it is positive (increasing).
OR
With or without a sketch:
Showing \(f({x_1}) > f(3)\) where \({x_1} < 3\) and \({x_1}\) is close to 3. (M1)
Showing \(f({x_2}) > f(3)\) where \({x_2} > 3\) and \({x_2}\) is close to 3. (M1)
Note: If a sketch of \(f(x)\) is drawn in this part of the question and \(x = 3\) is identified as a stationary point on the curve, then
(i) award, at most, (M1)(A1)(M1)(M0) if the stationary point has been found;
(ii) award, at most, (M0)(A0)(M1)(M0) if the stationary point has not been previously found.
Since the gradients go from negative (decreasing) through zero to positive (increasing) it is a local minimum (R1)(AG)
Note: Only award (R1) if the first two marks have been awarded ie \(f'(3)\) has been shown to be equal to \(0\).[5 marks]
(A1)(A1)(A1)(A1)
Notes: Award (A1) for labelled axes and indication of scale on both axes.
Award (A1) for smooth curve with correct shape.
Award (A1) for local minima in \({2^{{\text{nd}}}}\) and \({4^{{\text{th}}}}\) quadrants.
Award (A1) for y intercept \((0, 20)\) seen and labelled. Accept \(20\) on \(y\)–axis.
Do not award the third (A1) mark if there is a turning point on the \(x\)-axis.
If the derivative function is sketched then award, at most, (A1)(A0)(A0)(A0).
For a smooth curve (with correct shape) there should be ONE continuous thin line, no part of which is straight and no (one to many) mappings of \(x\).[4 marks]
\((0, 20)\) (G1)(G1)
Note: If parentheses are omitted award (G0)(G1).
OR
\(x = 0,{\text{ }}y = 20\) (G1)(G1)
Note: If the derivative function is sketched in part (d), award (G1)(ft)(G1)(ft) for \((–1.12, 12.2)\).[2 marks]
\(f'(2) = 3{(2)^3} – 3{(2)^2} – 18(2)\) (M1)
Notes: Award (M1) for substituting \(x = 2\) into their \(f'(x)\).
\( = – 24\) (A1)(ft)(G2)[2 marks]
(i) Gradient of perpendicular \( = \frac{1}{{24}}\) \((0.0417, 0.041666…)\) (A1)(ft)(G1)
Note: Follow through from part (f).
(ii) \(y + 12 = \frac{1}{{24}}(x – 2)\) (M1)(M1)
Note: Award (M1) for correct substitution of \((2, –12)\), (M1) for correct substitution of their perpendicular gradient into equation of line.
OR
\( – 12 = \frac{1}{{24}} \times 2 + d\) (M1)
\(d = – \frac{{145}}{{12}}\)
\(y = \frac{1}{{24}}x – \frac{{145}}{{12}}\) (M1)
Note: Award (M1) for correct substitution of \((2, –12)\) and gradient into equation of a straight line, (M1) for correct substitution of the perpendicular gradient and correct substitution of \(d\)into equation of line.
\(b = – 24,{\text{ }}c = – 290\) (A1)(ft)(A1)(ft)(G3)
Note: Follow through from parts (f) and g(i).
To award (ft) marks, \(b\) and \(c\) must be integers.
Where candidate has used \(0.042\) from g(i), award (A1)(ft) for \(–288\).[5 marks]
Question
The following diagram shows two triangles, OBC and OBA, on a set of axes. Point C lies on the \(y\)-axis, and O is the origin.
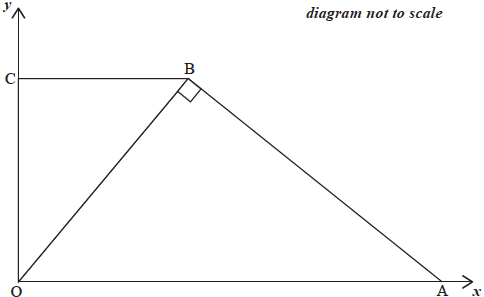
The equation of the line BC is \(y = 4\).
Write down the coordinates of point C.[1]
The \(x\)-coordinate of point B is \(a\).
(i) Write down the coordinates of point B;
(ii) Write down the gradient of the line OB.[2]
Point A lies on the \(x\)-axis and the line AB is perpendicular to line OB.
(i) Write down the gradient of line AB.
(ii) Show that the equation of the line AB is \(4y + ax – {a^2} – 16 = 0\).[4]
The area of triangle AOB is three times the area of triangle OBC.
Find an expression, in terms of a, for
(i) the area of triangle OBC;
(ii) the x-coordinate of point A.[3]
Calculate the value of \(a\).[2]
Answer/Explanation
Markscheme
\((0,{\text{ }}4)\) (A1)
Notes: Accept \(x = 0,{\text{ }}y = 4\).
(i) \((a,{\text{ }}4)\) (A1)(ft)
Notes: Follow through from part (a).
(ii) \(\frac{4}{a}\) (A1)(ft)
Note: Follow through from part (b)(i).
(i) \( – \frac{a}{4}\) (A1)(ft)
Note: Follow through from part (b)(ii).
(ii) \(y = – \frac{a}{4}x + c\) (M1)
Note: Award (M1) for substitution of their gradient from part (c)(i) in the equation.
\(4 = – \frac{a}{4} \times a + c\)
\(c = \frac{1}{4} \times {a^2} + 4\)
\(y = – \frac{a}{4}x + \frac{1}{4}{a^2} + 4\) (A1)
OR
\(y – 4 = – \frac{a}{4}(x – a)\) (M1)
Note: Award (M1) for substitution of their gradient from part (c)(i) in the equation.
\(y = – \frac{{ax}}{4} + \frac{{{a^2}}}{4} + 4\) (A1)
\(4y = – ax + {a^2} + 16\)
\(4y + ax – {a^2} – 16 = 0\) (AG)
Note: Both the simplified and the not simplified equations must be seen for the final (A1) to be awarded.
(i) \(2a\) (A1)
(ii) \(\frac{{4x}}{2} = 3 \times 2a\) (M1)
Note: Award (M1) for correct equation.
\(x = 3a\) (A1)(ft)
Note: Follow through from part (d)(i).
OR
\(0 – 4 = – \frac{a}{4}(x – a)\) (M1)
Note: Award (M1) for correct substitution of their gradient and the coordinates of their point into the equation of a line.
\(\frac{{16}}{a} = x – a\)
\(x = a + \frac{{16}}{a}\) (A1)(ft)
Note: Follow through from parts (b)(i) and (c)(i).
OR
\(4 \times 0 + ax – {a^2} – 16 = 0\) (M1)
Note: Award (M1) for correct substitution of the coordinates of \({\text{A}}(x,{\text{ }}0)\) into the equation of line AB.
\(ax – {a^2} – 16 = 0\)
\(x = a + \frac{{16}}{a}\;\;\;\)OR\(\;\;\;x = \frac{{({a^2} + 16)}}{a}\) (A1)(G1)
\(4(0) + a(3a) – {a^2} – 16 = 0\) (M1)
Note: Award (M1) for correct substitution of their \(3a\) from part (d)(ii) into the equation of line AB.
OR
\(\frac{1}{2}\left( {a + \frac{{16}}{a}} \right) \times 4 = 3\left( {\frac{{4a}}{2}} \right)\) (M1)
Note: Award (M1) for area of triangle AOB (with their substituted \(a + \frac{{16}}{a}\) and 4) equated to three times their area of triangle AOB.
\(a = 2.83\;\;\;\left( {2.82842…,{\text{ }}2\sqrt 2 ,{\text{ }}\sqrt 8 } \right)\) (A1)(ft)(G1)
Note: Follow through from parts (d)(i) and (d)(ii).
Question
Consider the function \(f(x) = \frac{{96}}{{{x^2}}} + kx\), where \(k\) is a constant and \(x \ne 0\).
Write down \(f'(x)\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Show that \(k = 3\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f(2)\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f'(2)\)[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find the equation of the normal to the graph of \(y = f(x)\) at the point where \(x = 2\).
Give your answer in the form \(ax + by + d = 0\) where \(a,{\text{ }}b,{\text{ }}d \in \mathbb{Z}\).[3]
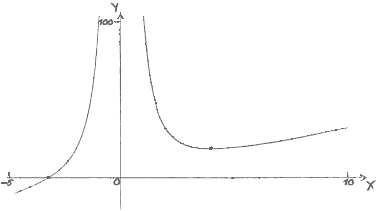
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Sketch the graph of \(y = f(x)\), for \( – 5 \leqslant x \leqslant 10\) and \( – 10 \leqslant y \leqslant 100\).[4]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Write down the coordinates of the point where the graph of \(y = f(x)\) intersects the \(x\)-axis.[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
State the values of \(x\) for which \(f(x)\) is decreasing.[2]
Answer/Explanation
Markscheme
\(\frac{{ – 192}}{{{x^3}}} + k\) (A1)(A1)(A1)
Note: Award (A1) for \(-192\), (A1) for \({x^{ – 3}}\), (A1) for \(k\) (only).
at local minimum \(f'(x) = 0\) (M1)
Note: Award (M1) for seeing \(f'(x) = 0\) (may be implicit in their working).
\(\frac{{ – 192}}{{{4^3}}} + k = 0\) (A1)
\(k = 3\) (AG)
Note: Award (A1) for substituting \(x = 4\) in their \(f'(x) = 0\), provided it leads to \(k = 3\). The conclusion \(k = 3\) must be seen for the (A1) to be awarded.
\(\frac{{96}}{{{2^2}}} + 3(2)\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in \(f(x)\).
\( = 30\) (A1)(G2)
\(\frac{{ – 192}}{{{2^3}}} + 3\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in their \(f'(x)\).
\( = – 21\) (A1)(ft)(G2)
Note: Follow through from part (a).
\(y – 30 = \frac{1}{{21}}(x – 2)\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their \(\frac{1}{{21}}\) seen, (M1) for the correct substitution of their point and their normal gradient in equation of a line.
Follow through from part (c) and part (d).
OR
gradient of normal \( = \frac{1}{{21}}\) (A1)(ft)
\(30 = \frac{1}{{21}} \times 2 + c\) (M1)
\(c = 29\frac{{19}}{{21}}\)
\(y = \frac{1}{{21}}x + 29\frac{{19}}{{21}}\;\;\;(y = 0.0476x + 29.904)\)
\(x – 21y + 628 = 0\) (A1)(ft)(G2)
Notes: Accept equivalent answers.
(A1)(A1)(A1)(A1)
Notes: Award (A1) for correct window (at least one value, other than zero, labelled on each axis), the axes must also be labelled; (A1) for a smooth curve with the correct shape (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis), on the given domain; (A1) for axis intercept in approximately the correct position (nearer \(-5\) than zero); (A1) for local minimum in approximately the correct position (first quadrant, nearer the \(y\)-axis than \(x = 10\)).
If there is no scale, award a maximum of (A0)(A1)(A0)(A1) – the final (A1) being awarded for the zero and local minimum in approximately correct positions relative to each other.
\(( – 3.17,{\text{ }}0)\;\;\;\left( {( – 3.17480 \ldots ,{\text{ 0)}}} \right)\) (G1)(G1)
Notes: If parentheses are omitted award (G0)(G1)(ft).
Accept \(x = – 3.17,{\text{ }}y = 0\). Award (G1) for \(-3.17\) seen.
\(0 < x \leqslant 4{\text{ or }}0 < x < 4\) (A1)(A1)
Notes: Award (A1) for correct end points of interval, (A1) for correct notation (note: lower inequality must be strict).
Award a maximum of (A1)(A0) if \(y\) or \(f(x)\) used in place of \(x\).
Question
The line \({L_1}\) has equation \(2y – x – 7 = 0\) and is shown on the diagram.
The point A has coordinates \((1,{\text{ }}4)\).
The point C has coordinates \((5,{\text{ }}12)\). M is the midpoint of AC.
The straight line, \({L_2}\), is perpendicular to AC and passes through M.
The point D is the intersection of \({L_1}\) and \({L_2}\).
The length of MD is \(\frac{{\sqrt {45} }}{2}\).
The point B is such that ABCD is a rhombus.
Show that A lies on \({L_1}\).[2]
Find the coordinates of M.[2]
Find the length of AC.[2]
Show that the equation of \({L_2}\) is \(2y + x – 19 = 0\).[5]
Find the coordinates of D.[2]
Write down the length of MD correct to five significant figures.[1]
Find the area of ABCD.[3]
Answer/Explanation
Markscheme
\(2 \times 4 – 1 – 7 = 0\) (or equivalent) (R1)
Note: For (R1) accept substitution of \(x = 1\) or \(y = 4\) into the equation followed by a confirmation that \(y = 4\) or \(x = 1\).
(since the point satisfies the equation of the line,) A lies on \({L_1}\) (A1)
Note: Do not award (A1)(R0).[2 marks]
\(\frac{{1 + 5}}{2}\) OR \(\frac{{4 + 12}}{2}\) seen (M1)
Note: Award (M1) for at least one correct substitution into the midpoint formula.
\((3,{\text{ }}8)\) (A1)(G2)
Notes: Accept \(x = 3,{\text{ }}y = 8\).
Award (M1)(A0) for \(\left( {\frac{{1 + 5}}{2},{\text{ }}\frac{{4 + 12}}{2}} \right)\).
Award (G1) for each correct coordinate seen without working.[2 marks]
\(\sqrt {{{(5 – 1)}^2} + {{(12 – 4)}^2}} \) (M1)
Note: Award (M1) for a correct substitution into distance between two points formula.
\( = 8.94{\text{ }}\left( {4\sqrt 5 ,{\text{ }}\sqrt {80} ,{\text{ }}8.94427 \ldots } \right)\) (A1)(G2)[2 marks]
gradient of \({\text{AC}} = \frac{{12 – 4}}{{5 – 1}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = 2\) (A1)
Note: Award (M1)(A1) for gradient of \({\text{AC}} = 2\) with or without working
gradient of the normal \( = – \frac{1}{2}\) (M1)
Note: Award (M1) for the negative reciprocal of their gradient of AC.
\(y – 8 = – \frac{1}{2}(x – 3)\) OR \(8 = – \frac{1}{2}(3) + c\) (M1)
Note: Award (M1) for substitution of their point and gradient into straight line formula. This (M1) can only be awarded where \( – \frac{1}{2}\) (gradient) is correctly determined as the gradient of the normal to AC.
\(2y – 16 = – (x – 3)\) OR \( – 2y + 16 = x – 3\) OR \(2y = – x + 19\) (A1)
Note: Award (A1) for correctly removing fractions, but only if their equation is equivalent to the given equation.
\(2y + x – 19 = 0\) (AG)
Note: The conclusion \(2y + x – 19 = 0\) must be seen for the (A1) to be awarded.
Where the candidate has shown the gradient of the normal to \({\text{AC}} = – 0.5\), award (M1) for \(2(8) + 3 – 19 = 0\) and (A1) for (therefore) \(2y + x – 19 = 0\).
Simply substituting \((3,{\text{ }}8)\) into the equation of \({L_2}\) with no other prior working, earns no marks.[5 marks]
\((6,{\text{ }}6.5)\) (A1)(A1)(G2)
Note: Award (A1) for 6, (A1) for 6.5. Award a maximum of (A1)(A0) if answers are not given as a coordinate pair. Accept \(x = 6,{\text{ }}y = 6.5\).
Award (M1)(A0) for an attempt to solve the two simultaneous equations \(2y – x – 7 = 0\) and \(2y + x – 19 = 0\) algebraically, leading to at least one incorrect or missing coordinate.[2 marks]
3.3541 (A1)
Note: Answer must be to 5 significant figures.[1 mark]
\(2 \times \frac{1}{2} \times \sqrt {80} \times \frac{{\sqrt {45} }}{2}\) (M1)(M1)
Notes: Award (M1) for correct substitution into area of triangle formula.
If their triangle is a quarter of the rhombus then award (M1) for multiplying their triangle by 4.
If their triangle is a half of the rhombus then award (M1) for multiplying their triangle by 2.
OR
\(\frac{1}{2} \times \sqrt {80} \times \sqrt {45} \) (M1)(M1)
Notes: Award (M1) for doubling MD to get the diagonal BD, (M1) for correct substitution into the area of a rhombus formula.
Award (M1)(M1) for \(\sqrt {80} \times \) their (f).
\( = 30\) (A1)(ft)(G3)
Notes: Follow through from parts (c) and (f).
\(8.94 \times 3.3541 = 29.9856 \ldots \)[3 marks]