Question
Mal is shopping for a school trip. He buys \(50\) tins of beans and \(20\) packets of cereal. The total cost is \(260\) Australian dollars (\({\text{AUD}}\)).
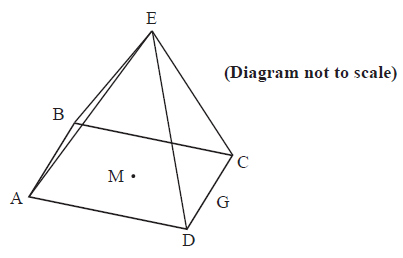
The triangular faces of a square based pyramid, \({\text{ABCDE}}\), are all inclined at \({70^ \circ }\) to the base. The edges of the base \({\text{ABCD}}\) are all \(10{\text{ cm}}\) and \({\text{M}}\) is the centre. \({\text{G}}\) is the mid-point of \({\text{CD}}\).
Write down an equation showing this information, taking \(b\) to be the cost of one tin of beans and \(c\) to be the cost of one packet of cereal in \({\text{AUD}}\).[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Write down another equation to represent this information.[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Find the cost of one tin of beans.[2]
(i) Sketch the graphs of the two equations from parts (a) and (b).
(ii) Write down the coordinates of the point of intersection of the two graphs.[4]
Using the letters on the diagram draw a triangle showing the position of a \({70^ \circ }\) angle.[1]
Show that the height of the pyramid is \(13.7{\text{ cm}}\), to 3 significant figures.[2]
Calculate
(i) the length of \({\text{EG}}\);
(ii) the size of angle \({\text{DEC}}\).[4]
Find the total surface area of the pyramid.[2]
Find the volume of the pyramid.[2]
Answer/Explanation
Markscheme
\(50b + 20c = 260\) (A1)[1 mark]
\(12b + 6c = 66\) (A1)[1 mark]
Solve to get \(b = 4\) (M1)(A1)(ft)(G2)
Note: (M1) for attempting to solve the equations simultaneously.[2 marks]
(i)
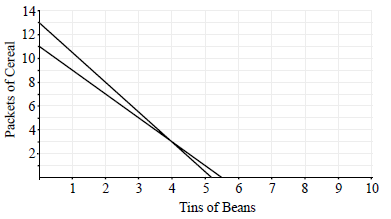(A1)(A1)(A1)
Notes: Award (A1) for labels and some idea of scale, (A1)(ft)(A1)(ft) for each line.
The axis can be reversed.
(ii) \((4,3)\) or \((3,4)\) (A1)(ft)
Note: Accept \(b = 4\), \(c = 3\)[4 marks]
(A1)[1 mark]
\(\tan 70 = \frac{h}{5}\) (M1)
\(h = 5\tan 70 = 13.74\) (A1)
\(h = 13.7{\text{ cm}}\) (AG)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
(i) \({\text{E}}{{\text{G}}^2} = {5^2} + {13.7^2}\) OR \({5^2} + {(5\tan 70)^2}\) (M1)
(UP) \({\text{EG}} = 14.6{\text{ cm}}\) (A1)(G2)
(ii) \({\text{DEC}} = 2 \times {\tan ^{ – 1}}\left( {\frac{5}{{14.6}}} \right)\) (M1)
\( = {37.8^ \circ }\) (A1)(ft)(G2)[4 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Area}} = 10 \times 10 + 4 \times 0.5 \times 10 \times 14.619\) (M1)
(UP) \( = 392{\text{ c}}{{\text{m}}^2}\) (A1)(ft)(G2)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Volume}} = \frac{1}{3} \times 10 \times 10 \times 13.7\) (M1)
(UP) \( = 457{\text{ c}}{{\text{m}}^3}\) (\(458{\text{ c}}{{\text{m}}^3}\)) (A1)(G2)[2 marks]
Question
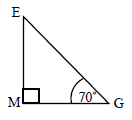
Amir needs to construct an isosceles triangle \({\text{ABC}}\) whose area is \(100{\text{ cm}}^2\). The equal sides, \({\text{AB}}\) and \({\text{BC}}\), are \(20{\text{ cm}}\) long.
Sylvia is making a square-based pyramid. Each triangle has a base of length \(12{\text{ cm}}\) and a height of \(10{\text{ cm}}\).
Angle \({\text{ABC}}\) is acute. Show that the angle \({\text{ABC}}\) is \({30^ \circ }\).[2]
Find the length of \({\text{AC}}\).[3]
Show that the height of the pyramid is \(8{\text{ cm}}\).[2]
\({\text{M}}\) is the midpoint of the base of one of the triangles and \({\text{O}}\) is the apex of the pyramid.
Find the angle that the line \({\text{MO}}\) makes with the base of the pyramid.[3]
Calculate the volume of the pyramid.[2]
Daniel wants to make a rectangular prism with the same volume as that of Sylvia’s pyramid. The base of his prism is to be a square of side \(10{\text{ cm}}\). Calculate the height of the prism.[2]
Answer/Explanation
Markscheme
\(\frac{1}{2}{20^2}\sin B = 100\) (M1)(A1)
\(B = {30^ \circ }\) (AG)
Note: (M1) for correct substituted formula and (A1) for correct substitution. \(B = {30^ \circ }\) must be seen or previous (A1) mark is lost.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
\({\overline {{\text{AC}}} ^2} = 2 \times {20^2} – 2 \times {20^2} \times \cos {30^ \circ }\) (M1)(A1)
(UP) \(\overline {{\text{AC}}} = 10.4{\text{ cm}}\) (A1)(G2)
Note: (M1) for using cosine rule, (A1) for correct substitution. Last (A1) is for the correct answer. Accept use of sine rule or any correct method e.g. \({\text{AC}} = 2 \times 20\sin {15^ \circ }\) .[3 marks]
\({x^2} + {6^2} = {10^2}\) (A1)(M1)
\(x = 8{\text{ cm}}\) (AG)
Note: (A1) for \(6\) (or \(36\)) seen and (M1) for using Pythagoras with correct substitution. \(x = 8\) must be seen or previous (M1) mark is lost.[2 marks]
\(\cos \beta = \frac{6}{{10}}\) (M1)(A1)
\(\beta = {53.1^ \circ }\) (A1)(G2)
OR equivalent
Note: (M1) for use of trigonometric ratio with numbers from question. (A1) for use of correct numbers, and (A1) for correct answer.[3 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
\(vol = \frac{{{{12}^2} \times 8}}{3}\) (M1)
(UP) \( = 384{\text{ c}}{{\text{m}}^3}\) (A1)(G2)
Note: (M1) for correct formula and correct substitution, (A1) for correct answer.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
Let h be the height
\({10^2}h = 384\) (M1)
(UP) \( = 3.84{\text{ cm}}\) (A1)(ft)(G2)
Note: (M1) for correct formula and correct substitution, (A1) for correct answer. (ft) from answer to part (c).[2 marks]
Question
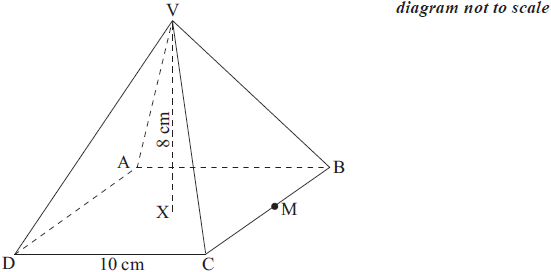
The diagram below shows a square based right pyramid. ABCD is a square of side 10 cm. VX is the perpendicular height of 8 cm. M is the midpoint of BC.
In a mountain region there appears to be a relationship between the number of trees growing in the region and the depth of snow in winter. A set of 10 areas was chosen, and in each area the number of trees was counted and the depth of snow measured. The results are given in the table below.
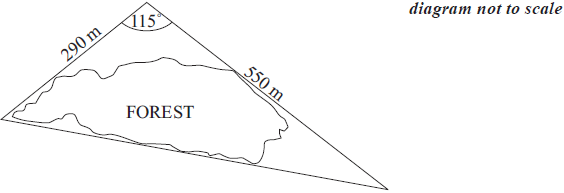
A path goes around a forest so that it forms the three sides of a triangle. The lengths of two sides are 550 m and 290 m. These two sides meet at an angle of 115°. A diagram is shown below.
Write down the length of XM.[1]
Use your graphic display calculator to find the standard deviation of the number of trees.[1]
Calculate the length of VM.[2]
Calculate the angle between VM and ABCD.[2]
Calculate the length of the third side of the triangle. Give your answer correct to the nearest 10 m.[4]
Calculate the area enclosed by the path that goes around the forest.[3]
Inside the forest a second path forms the three sides of another triangle named ABC. Angle BAC is 53°, AC is 180 m and BC is 230 m.
Calculate the size of angle ACB.[4]
Answer/Explanation
Markscheme
UP applies in this question
(UP) XM = 5 cm (A1)[1 mark]
16.8 (G1)[1 mark]
UP applies in this question
VM2 = 52 + 82 (M1)
Note: Award (M1) for correct use of Pythagoras Theorem.
(UP) VM = \(\sqrt{89}\) = 9.43 cm (A1)(ft)(G2)[2 marks]
\(\tan {\text{VMX}} = \frac{8}{5}\) (M1)
Note: Other trigonometric ratios may be used.
\({\rm{V\hat MX}} = 58.0^\circ \) (A1)(ft)(G2)[2 marks]
UP applies in this question
l2 = 2902 + 5502 − 2 × 290 × 550 × cos115° (M1)(A1)
Note: Award (M1) for substituted cosine rule formula, (A1) for correct substitution.
l = 722 (A1)(G2)
(UP) = 720 m (A1)
Note: If 720 m seen without working award (G3).
The final (A1) is awarded for the correct rounding of their answer.[4 marks]
UP applies in this question
\({\text{Area}} = \frac{1}{2} \times 290 \times 550 \times \sin 115\) (M1)(A1)
Note: Award (M1) for substituted correct formula (A1) for correct substitution.
(UP) = \(72\,300{\text{ }}{{\text{m}}^2}\) (A1)(G2)[3 marks]
\(\frac{{180}}{{\sin {\text{B}}}} = \frac{{230}}{{\sin 53}}\) (M1)(A1)
Note: Award (M1) for substituted sine rule formula, (A1) for correct substitution.
B = 38.7° (A1)(G2)
\({\operatorname{A\hat CB}} = 180 – (53^\circ + 38.7^\circ )\)
\( = 88.3^\circ \) (A1)(ft) [4 marks]
Question
A dog food manufacturer has to cut production costs. She wishes to use as little aluminium as possible in the construction of cylindrical cans. In the following diagram, h represents the height of the can in cm and x, the radius of the base of the can in cm.
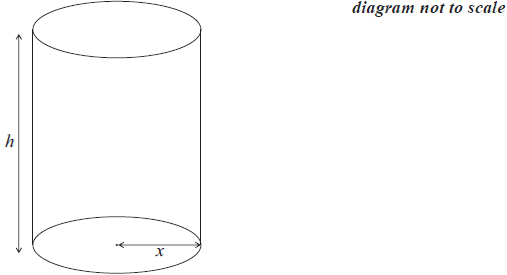
The volume of the dog food cans is 600 cm3.
Show that \(h = \frac{{600}}{{\pi {x^2}}}\).[2]
Find an expression for the curved surface area of the can, in terms of x. Simplify your answer.[2]
Hence write down an expression for A, the total surface area of the can, in terms of x.[2]
Differentiate A in terms of x.[3]
Find the value of x that makes A a minimum.[3]
Calculate the minimum total surface area of the dog food can.[2]
Answer/Explanation
Markscheme
\(600 = \pi x^2 h\) (M1)(A1)
\(\frac{600}{\pi x^2} = h\) (AG)
Note: Award (M1) for correct substituted formula, (A1) for correct substitution. If answer given not shown award at most (M1)(A0).[2 marks]
\(C = 2 \pi x \frac{600}{\pi x^2}\) (M1)
\(C = \frac{1200}{x}\) (or 1200x–1) (A1)
Note: Award (M1) for correct substitution in formula, (A1) for correct simplification.[??? marks]
\(A = 2 \pi x^2 + 1200x^{-1}\) (A1)(A1)(ft)
Note: Award (A1) for multiplying the area of the base by two, (A1) for adding on their answer to part (b) (i).
For both marks to be awarded answer must be in terms of x.
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 4\pi x – \frac{{1200}}{{{x^2}}}\) (A1)(ft)(A1)(ft)(A1)(ft)
Notes: Award (A1) for \(4 \pi x\), (A1) for \(-1200\), (A1) for \(x^{-2}\). Award at most (A2) if any extra term is written. Follow through from their part (b) (ii).
\(4 \pi x – \frac{1200}{x^2} = 0\) (M1)(M1)
\(x^3 = \frac{1200}{4 \pi}\) (or equivalent)
\(x = 4.57\) (A1)(ft)(G2)
Note: Award (M1) for using their derivative, (M1) for setting the derivative to zero, (A1)(ft) for answer.
Follow through from their derivative.
Last mark is lost if value of x is zero or negative.[3 marks]
\(A = 2 \pi (4.57)^2 + 1200(4.57)^{-1}\) (M1)
\(A = 394\) (A1)(ft)(G2)
Note: Follow through from their answers to parts (b) (ii) and (d).[2 marks]
Question
The Great Pyramid of Cheops in Egypt is a square based pyramid. The base of the pyramid is a square of side length 230.4 m and the vertical height is 146.5 m. The Great Pyramid is represented in the diagram below as ABCDV . The vertex V is directly above the centre O of the base. M is the midpoint of BC.
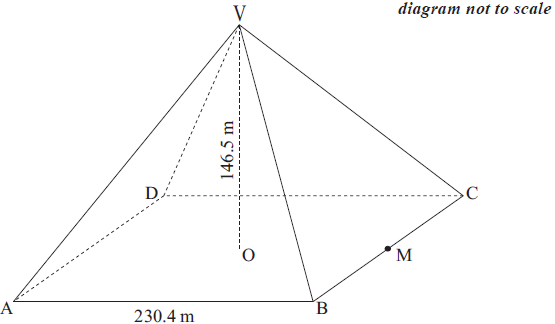
(i) Write down the length of OM .
(ii) Find the length of VM .[3]
Find the area of triangle VBC .[2]
Calculate the volume of the pyramid.[2]
Show that the angle between the line VM and the base of the pyramid is 52° correct to 2 significant figures.[2]
Ahmed is at point P , a distance x metres from M on horizontal ground, as shown in the following diagram. The size of angle VPM is 27° . Q is a point on MP .
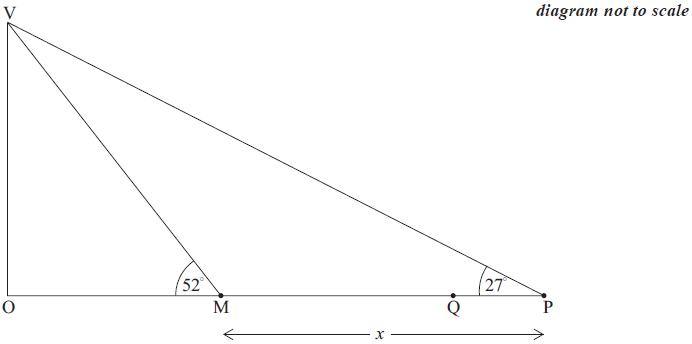
Write down the size of angle VMP .[1]
Ahmed is at point P , a distance x metres from M on horizontal ground, as shown in the following diagram. The size of angle VPM is 27° . Q is a point on MP .
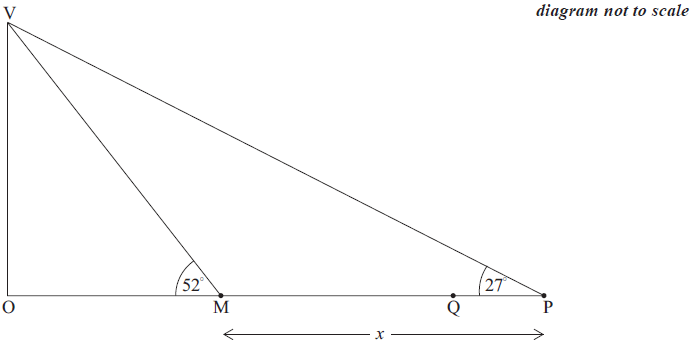
Using your value of VM from part (a)(ii), find the value of x.[4]
Ahmed is at point P , a distance x metres from M on horizontal ground, as shown in the following diagram. The size of angle VPM is 27° . Q is a point on MP .
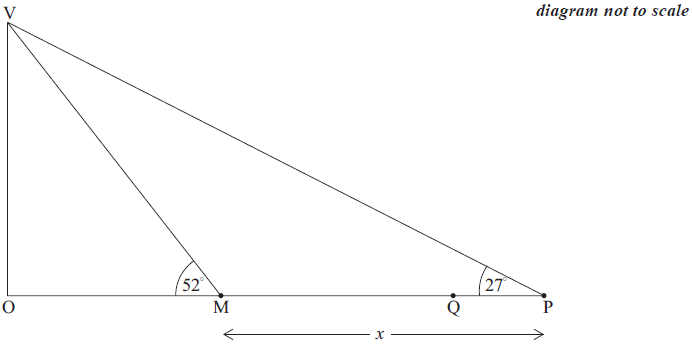
Ahmed walks 50 m from P to Q.
Find the length of QV, the distance from Ahmed to the vertex of the pyramid.[4]
Answer/Explanation
Markscheme
(i) 115.2 (m) (A1)
Note: Accept 115 (m)
(ii) \(\sqrt{(146.5^2 + 115.2^2)}\) (M1)
Note: Award (M1) for correct substitution.
186 (m) (186.368…) (A1)(ft)(G2)
Note: Follow through from part (a)(i).[3 marks]
\(\frac{1}{2} \times 230.4 \times 186.368…\) (M1)
Note: Award (M1) for correct substitution in area of the triangle formula.
21500 m2 (21469.6…m2) (A1)(ft)(G2)
Notes: The final answer is 21500 m2; units are required. Accept 21400 m2 for use of 186 m and/or 115 m.[2 marks]
\(\frac{1}{3} \times 230.4^2 \times 146.5\) (M1)
Note: Award (M1) for correct substitution in volume formula.
2590000 m3 (2592276.48 m3) (A1)(G2)
Note: The final answer is 2590000 m3; units are required but do not penalise missing or incorrect units if this has already been penalised in part (b). [2 marks]
\(\tan^{-1}\left( {\frac{{146.5}}{{115.2}}} \right)\) (M1)
Notes: Award (M1) for correct substituted trig ratio. Accept alternate correct trig ratios.
= 51.8203…= 52° (A1)(AG)
Notes: Both the unrounded answer and the final answer must be seen for the (A1) to be awarded. Accept 51.96° = 52°, 51.9° = 52° or 51.7° = 52°
128° (A1)[1 mark]
\(\frac{{186.368}}{{\sin27}} = \frac{{x}}{{\sin25}}\) (A1)(M1)(A1)(ft)
Notes: Award (A1)(ft) for their angle MVP seen, follow through from their part (e). Award (M1) for substitution into sine formula, (A1) for correct substitutions. Follow through from their VM and their angle VMP.
x = 173 (m) (173.490…) (A1)(ft)(G3)
Note: Accept 174 from use of 186.4.[4 marks]
VQ2 = (186.368…)2 + (123.490…)2 − 2 × (186.368…) × (123.490…) × cos128 (A1)(ft)(M1)(A1)(ft)
Notes: Award (A1)(ft) for 123.490…(123) seen, follow through from their x (PM) in part (f), (M1) for substitution into cosine formula, (A1)(ft) for correct substitutions. Follow through from their VM and their angle VMP.
OR
173.490… − 50 = 123.490… (123) (A1)(ft)
115.2 + 123.490… = 238.690… (A1)(ft)
\(\text{VQ} = \sqrt{(146.5^2 + 238.690…^2)}\) (M1)
VQ = 280 (m) (280.062…) (A1)(ft)(G3)
Note: Accept 279 (m) from use of 3 significant figure answers.[4 marks]
Question
A lobster trap is made in the shape of half a cylinder. It is constructed from a steel frame with netting pulled tightly around it. The steel frame consists of a rectangular base, two semicircular ends and two further support rods, as shown in the following diagram.
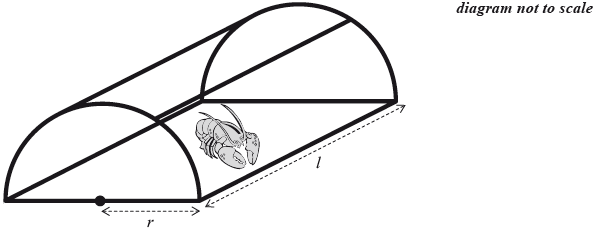
The semicircular ends each have radius \(r\) and the support rods each have length \(l\).
Let \(T\) be the total length of steel used in the frame of the lobster trap.
Write down an expression for \(T\) in terms of \(r\), \(l\) and \(\pi \).[3]
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Write down an equation for the volume of the lobster trap in terms of \(r\), \(l\) and \(\pi \).[3]
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Show that \(T = (2\pi + 4)r + \frac{6}{{\pi {r^2}}}\).[2]
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Find \(\frac{{{\text{d}}T}}{{{\text{d}}r}}\).[3]
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Show that the value of \(r\) for which \(T\) is a minimum is \(0.719 {\text{ m}}\), correct to three significant figures.[2]
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Calculate the value of \(l\) for which \(T\) is a minimum.[2]
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Calculate the minimum value of \(T\).[2]
Answer/Explanation
Markscheme
\(2\pi r + 4r + 4l\) (A1)(A1)(A1)
Notes: Award (A1) for \(2\pi r\) (“\(\pi \)” must be seen), (A1) for \(4r\), (A1) for \(4l\). Accept equivalent forms. Accept \(T = 2\pi r + 4r + 4l\). Award a maximum of (A1)(A1)(A0) if extra terms are seen.[3 marks]
\(0.75 = \frac{{\pi {r^2}l}}{2}\) (A1)(A1)(A1)
Notes: Award (A1) for their formula equated to \(0.75\), (A1) for \(l\) substituted into volume of cylinder formula, (A1) for volume of cylinder formula divided by \(2\).
If “\(\pi \)” not seen in part (a) accept use of \(3.14\) or greater accuracy. Award a maximum of (A1)(A1)(A0) if extra terms are seen.[3 marks]
\(T = 2\pi r + 4r + 4\left( {\frac{{1.5}}{{\pi {r^2}}}} \right)\) (A1)(ft)(A1)
\( = (2\pi + 4)r + \frac{6}{{\pi {r^2}}}\) (AG)
Notes: Award (A1)(ft) for correct rearrangement of their volume formula in part (b) seen, award (A1) for the correct substituted formula for \(T\). The final line must be seen, with no incorrect working, for this second (A1) to be awarded.[2 marks]
\(\frac{{{\text{d}}T}}{{{\text{d}}r}} = 2\pi + 4 – \frac{{12}}{{\pi {r^3}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi + 4\), (A1) for \(\frac{{ – 12}}{\pi }\), (A1) for \({r^{ – 3}}\).
Accept 10.3 (10.2832…) for \(2\pi + 4\), accept \(–3.82\) \(–3.81971…\) for \(\frac{{ – 12}}{\pi }\). Award a maximum of (A1)(A1)(A0) if extra terms are seen.[3 marks]
\(2\pi + 4 – \frac{{12}}{{\pi {r^3}}} = 0\) OR \(\frac{{{\text{d}}T}}{{{\text{d}}r}} = 0\) (M1)
Note: Award (M1) for setting their derivative equal to zero.
\(r = 0.718843 \ldots \) OR \(\sqrt[3]{{0.371452 \ldots }}\) OR \(\sqrt[3]{{\frac{{12}}{{\pi (2\pi + 4)}}}}\) OR \(\sqrt[3]{{\frac{{3.81971}}{{10.2832 \ldots }}}}\) (A1)
\(r = 0.719{\text{ (m)}}\) (AG)
Note: The rounded and unrounded or formulaic answers must be seen for the final (A1) to be awarded. The use of \(3.14\) gives an unrounded answer of \(r = 0.719039 \ldots \).[2 marks]
\(0.75 = \frac{{\pi \times {{(0.719)}^2}l}}{2}\) (M1)
Note: Award (M1) for substituting \(0.719\) into their volume formula. Follow through from part (b).
\(l = 0.924{\text{ (m)}}\) \((0.923599 \ldots )\) (A1)(ft)(G2)[2 marks]
\(T = (2\pi + 4) \times 0.719 + \frac{6}{{\pi {{(0.719)}^2}}}\) (M1)
Notes: Award (M1) for substituting \(0.719\) in their expression for \(T\). Accept alternative methods, for example substitution of their \(l\) and \(0.719\) into their part (a) (for which the answer is \(11.08961024\)). Follow through from their answer to part (a).
\( = 11.1{\text{ (m)}}\) \((11.0880 \ldots )\) (A1)(ft)(G2)
Question
A parcel is in the shape of a rectangular prism, as shown in the diagram. It has a length \(l\) cm, width \(w\) cm and height of \(20\) cm.
The total volume of the parcel is \(3000{\text{ c}}{{\text{m}}^3}\).
Express the volume of the parcel in terms of \(l\) and \(w\).[1]
Show that \(l = \frac{{150}}{w}\).[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
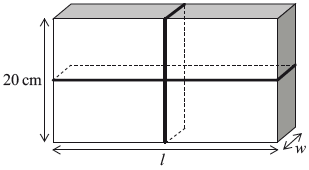
Show that the length of string, \(S\) cm, required to tie up the parcel can be written as
\[S = 40 + 4w + \frac{{300}}{w},{\text{ }}0 < w \leqslant 20.\][2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Draw the graph of \(S\) for \(0 < w \leqslant 20\) and \(0 < S \leqslant 500\), clearly showing the local minimum point. Use a scale of \(2\) cm to represent \(5\) units on the horizontal axis \(w\) (cm), and a scale of \(2\) cm to represent \(100\) units on the vertical axis \(S\) (cm).[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find \(\frac{{{\text{d}}S}}{{{\text{d}}w}}\).[3]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the value of \(w\) for which \(S\) is a minimum.[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Write down the value, \(l\), of the parcel for which the length of string is a minimum.[1]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the minimum length of string required to tie up the parcel.[2]
Answer/Explanation
Markscheme
\(20lw\) OR \(V = 20lw\) (A1)[1 mark]
\(3000 = 20lw\) (M1)
Note: Award (M1) for equating their answer to part (a) to \(3000\).
\(l = \frac{{3000}}{{20w}}\) (M1)
Note: Award (M1) for rearranging equation to make \(l\) subject of the formula. The above equation must be seen to award (M1).
OR
\(150 = lw\) (M1)
Note: Award (M1) for division by \(20\) on both sides. The above equation must be seen to award (M1).
\(l = \frac{{150}}{w}\) (AG)[2 marks]
\(S = 2l + 4w + 2(20)\) (M1)
Note: Award (M1) for setting up a correct expression for \(S\).
\(2\left( {\frac{{150}}{w}} \right) + 4w + 2(20)\) (M1)
Notes: Award (M1) for correct substitution into the expression for \(S\). The above expression must be seen to award (M1).
\( = 40 + 4w + \frac{{300}}{w}\) (AG)[2 marks]
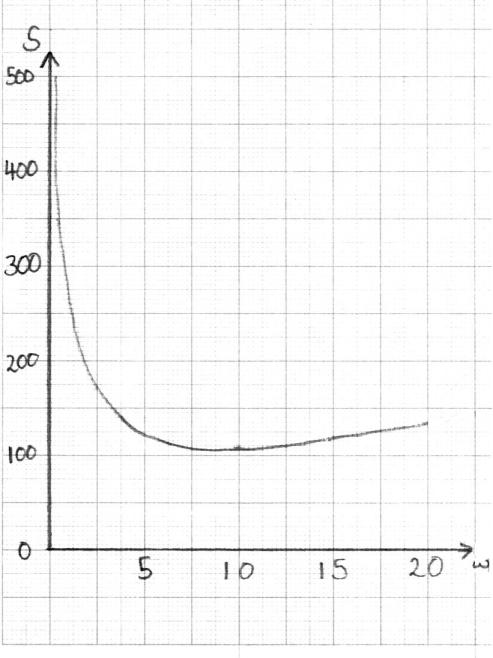(A1)(A1)(A1)(A1)
Note: Award (A1) for correct scales, window and labels on axes, (A1) for approximately correct shape, (A1) for minimum point in approximately correct position, (A1) for asymptotic behaviour at \(w = 0\).
Axes must be drawn with a ruler and labeled \(w\) and \(S\).
For a smooth curve (with approximately correct shape) there should be one continuous thin line, no part of which is straight and no (one-to-many) mappings of \(w\).
The \(S\)-axis must be an asymptote. The curve must not touch the \(S\)-axis nor must the curve approach the asymptote then deviate away later.[4 marks]
\(4 – \frac{{300}}{{{w^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(4\), (A1) for \(-300\), (A1) for \(\frac{1}{{{w^2}}}\) or \({w^{ – 2}}\). If extra terms present, award at most (A1)(A1)(A0).[3 marks]
\(4 – \frac{{300}}{{{w^2}}} = 0\) OR \(\frac{{300}}{{{w^2}}} = 4\) OR \(\frac{{{\text{d}}S}}{{{\text{d}}w}} = 0\) (M1)
Note: Award (M1) for equating their derivative to zero.
\(w = 8.66{\text{ }}\left( {\sqrt {75} ,{\text{ 8.66025}} \ldots } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).[2 marks]
\(17.3 \left( {\frac{{150}}{{\sqrt {75} }},{\text{ 17.3205}} \ldots } \right)\) (A1)(ft)
Note: Follow through from their answer to part (f).[1 mark]
\(40 + 4\sqrt {75} + \frac{{300}}{{\sqrt {75} }}\) (M1)
Note: Award (M1) for substitution of their answer to part (f) into the expression for \(S\).
\( = 110{\text{ (cm) }}\left( {40 + 40\sqrt 3 ,{\text{ 109.282}} \ldots } \right)\) (A1)(ft)(G2)
Note: Do not accept \(109\).
Follow through from their answers to parts (f) and (g).[2 marks]
Question
The front view of the edge of a water tank is drawn on a set of axes shown below.
The edge is modelled by \(y = a{x^2} + c\).
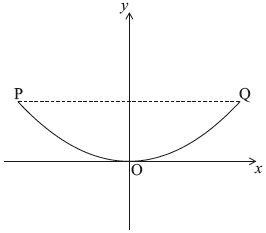
Point \({\text{P}}\) has coordinates \((-3, 1.8)\), point \({\text{O}}\) has coordinates \((0, 0)\) and point \({\text{Q}}\) has coordinates \((3, 1.8)\).
Write down the value of \(c\).[1]
Find the value of \(a\).[2]
Hence write down the equation of the quadratic function which models the edge of the water tank.[1]
The water tank is shown below. It is partially filled with water.
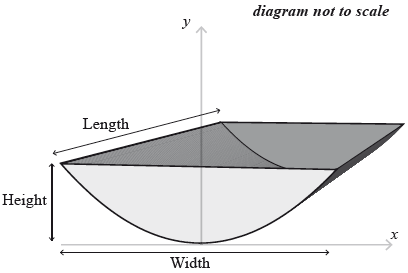
Calculate the value of y when \(x = 2.4{\text{ m}}\).[2]
The water tank is shown below. It is partially filled with water.
State what the value of \(x\) and the value of \(y\) represent for this water tank.[2]
The water tank is shown below. It is partially filled with water.
Find the value of \(x\) when the height of water in the tank is \(0.9\) m.[2]
The water tank is shown below. It is partially filled with water.
The water tank has a length of 5 m.
When the water tank is filled to a height of \(0.9\) m, the front cross-sectional area of the water is \({\text{2.55 }}{{\text{m}}^2}\).
(i) Calculate the volume of water in the tank.
The total volume of the tank is \({\text{36 }}{{\text{m}}^3}\).
(ii) Calculate the percentage of water in the tank.[2]
Answer/Explanation
Markscheme
\(0\) (A1)(G1)[1 mark]
\(1.8 = a{(3)^2} + 0\) (M1)
OR
\(1.8 = a{( – 3)^2} + 0\) (M1)
Note: Award (M1) for substitution of \(y = 1.8\) or \(x = 3\) and their value of \(c\) into equation. \(0\) may be implied.
\(a = 0.2\) \(\left( {\frac{1}{5}} \right)\) (A1)(ft)(G1)
Note: Follow through from their answer to part (a).
Award (G1) for a correct answer only.[2 marks]
\(y = 0.2{x^2}\) (A1)(ft)
Note: Follow through from their answers to parts (a) and (b).
Answer must be an equation.[1 mark]
\(0.2 \times {(2.4)^2}\) (M1)
\( = 1.15{\text{ (m)}}\) \((1.152)\) (A1)(ft)(G1)
Notes: Award (M1) for correctly substituted formula, (A1) for correct answer. Follow through from their answer to part (c).
Award (G1) for a correct answer only.[2 marks]
\(y\) is the height (A1)
positive value of \(x\) is half the width (or equivalent) (A1)[2 marks]
\(0.9 = 0.2{x^2}\) (M1)
Note: Award (M1) for setting their equation equal to \(0.9\).
\(x = \pm 2.12{\text{ (m)}}\) \(\left( { \pm \frac{3}{2}\sqrt 2 ,{\text{ }} \pm \sqrt {4.5} ,{\text{ }} \pm {\text{2.12132}} \ldots } \right)\) (A1)(ft)(G1)
Note: Accept \(2.12\). Award (G1) for a correct answer only.[2 marks]
(i) \(2.55 \times 5\) (M1)
Note: Award (M1) for correct substitution in formula.
\( = 12.8{\text{ (}}{{\text{m}}^3}{\text{)}}\) \(\left( {{\text{12.75 (}}{{\text{m}}^3}{\text{)}}} \right)\) (A1)(G2)[2 marks]
(ii) \(\frac{{12.75}}{{36}} \times 100\) (M1)
Note: Award (M1) for correct quotient multiplied by \(100\).
\( = 35.4 (\%)\) \((35.4166 \ldots )\) (A1)(ft)(G2)
Note: Award (G2) for \(35.6 (\%) (35.5555… (\%))\).
Follow through from their answer to part (g)(i).[2 marks]
Question
The following diagram shows a perfume bottle made up of a cylinder and a cone.
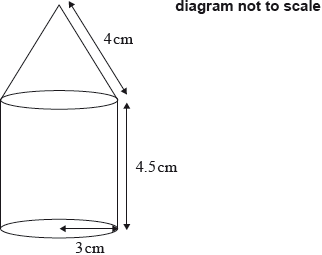
The radius of both the cylinder and the base of the cone is 3 cm.
The height of the cylinder is 4.5 cm.
The slant height of the cone is 4 cm.
(i) Show that the vertical height of the cone is \(2.65\) cm correct to three significant figures.
(ii) Calculate the volume of the perfume bottle.[6]
The bottle contains \({\text{125 c}}{{\text{m}}^{\text{3}}}\) of perfume. The bottle is not full and all of the perfume is in the cylinder part.
Find the height of the perfume in the bottle.[2]
Temi makes some crafts with perfume bottles, like the one above, once they are empty. Temi wants to know the surface area of one perfume bottle.
Find the total surface area of the perfume bottle.[4]
Temi covers the perfume bottles with a paint that costs 3 South African rand (ZAR) per millilitre. One millilitre of this paint covers an area of \({\text{7 c}}{{\text{m}}^{\text{2}}}\).
Calculate the cost, in ZAR, of painting the perfume bottle. Give your answer correct to two decimal places.[4]
Temi sells her perfume bottles in a craft fair for 325 ZAR each. Dominique from France buys one and wants to know how much she has spent, in euros (EUR). The exchange rate is 1 EUR = 13.03 ZAR.
Find the price, in EUR, that Dominique paid for the perfume bottle. Give your answer correct to two decimal places.[2]
Answer/Explanation
Markscheme
(i) \({x^2} + {3^2} = {4^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
Accept correct alternative method using trigonometric ratios.
\(x = 2.64575 \ldots \) (A1)
\(x = 2.65{\text{ }}({\text{cm}})\) (AG)
Note: The unrounded and rounded answer must be seen for the (A1) to be awarded.
OR
\(\sqrt {{4^2} – {3^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
\( = \sqrt 7 \) (A1)
\( = 2.65{\text{ (cm)}}\) (AG)
Note: The exact answer must be seen for the final (A1) to be awarded.
(ii) \(\pi \times {3^2} \times 4.5 + \frac{1}{3}\pi \times {3^2} \times 2.65\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula, (M1) for correct substitution into the volume of a cone formula, (M1) for adding both of their volumes.
\( = 152{\text{ c}}{{\text{m}}^3}\;\;\;(152.210 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}48.45\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G3)
\(\pi {3^2}h = 125\) (M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula.
Accept alternative methods. Accept \(4.43\) (\(4.42913 \ldots \)) from using rounded answers in \(h = \frac{{125 \times 4.5}}{{127}}\).
\(h = 4.42{\text{ (cm)}}\;\;\;\left( {4.42097 \ldots {\text{ (cm)}}} \right)\) (A1)(G2)
\(2\pi \times 3 \times 4.5 + \pi \times 3 \times 4 + \pi \times {3^2}\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into curved surface area of a cylinder formula, (M1) for correct substitution into the curved surface area of a cone formula, (M1) for adding the area of the base of the cylinder to the other two areas.
\( = 151{\text{ c}}{{\text{m}}^2}\;\;\;(150.796 \ldots {\text{ c}}{{\text{m}}^2},{\text{ }}48\pi {\text{ c}}{{\text{m}}^2})\) (A1)(G3)
\(\frac{{150.796 \ldots }}{7} \times 3\) (M1)(M1)
Notes: Award (M1) for dividing their answer to (c) by \(7\), (M1) for multiplying by \(3\). Accept equivalent methods.
\( = 64.63{\text{ (ZAR)}}\) (A1)(ft)(G2)
Notes: The (A1) is awarded for their correct answer, correctly rounded to 2 decimal places. Follow through from their answer to part (c). If rounded answer to part (c) is used the answer is \(64.71\) (ZAR).
\(\frac{{325}}{{13.03}}\) (M1)
Note: Award (M1) for dividing \(325\) by \(13.03\).
\( = 24.94{\text{ (EUR)}}\) (A1)(G2)
Note: The (A1) is awarded for the correct answer rounded to 2 decimal places, unless already penalized in part (d).
Question
The Great Pyramid of Giza in Egypt is a right pyramid with a square base. The pyramid is made of solid stone. The sides of the base are \(230\,{\text{m}}\) long. The diagram below represents this pyramid, labelled \({\text{VABCD}}\).
\({\text{V}}\) is the vertex of the pyramid. \({\text{O}}\) is the centre of the base, \({\text{ABCD}}\) . \({\text{M}}\) is the midpoint of \({\text{AB}}\). Angle \({\text{ABV}} = 58.3^\circ \) .
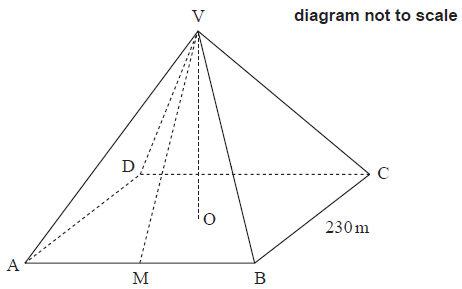
Show that the length of \({\text{VM}}\) is \(186\) metres, correct to three significant figures.[3]
Calculate the height of the pyramid, \({\text{VO}}\) .[2]
Find the volume of the pyramid.[2]
Write down your answer to part (c) in the form \(a \times {10^k}\) where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\) .[2]
Ahmad is a tour guide at the Great Pyramid of Giza. He claims that the amount of stone used to build the pyramid could build a wall \(5\) metres high and \(1\) metre wide stretching from Paris to Amsterdam, which are \(430\,{\text{km}}\) apart.
Determine whether Ahmad’s claim is correct. Give a reason.[4]
Ahmad and his friends like to sit in the pyramid’s shadow, \({\text{ABW}}\), to cool down.
At mid-afternoon, \({\text{BW}} = 160\,{\text{m}}\) and angle \({\text{ABW}} = 15^\circ .\)
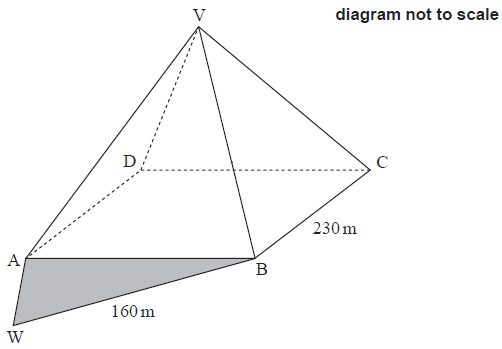
i) Calculate the length of \({\text{AW}}\) at mid-afternoon.
ii) Calculate the area of the shadow, \({\text{ABW}}\), at mid-afternoon.[6]
Answer/Explanation
Markscheme
\(\tan \,(58.3) = \frac{{{\text{VM}}}}{{115}}\) OR \(115 \times \tan \,(58.3^\circ )\) (A1)(M1)
Note: Award (A1) for \(115\,\,\left( {ie\,\frac{{230}}{2}} \right)\) seen, (M1) for correct substitution into trig formula.
\(\left( {{\text{VM}} = } \right)\,\,186.200\,({\text{m}})\) (A1)
\(\left( {{\text{VM}} = } \right)\,\,186\,({\text{m}})\) (AG)
Note: Both the rounded and unrounded answer must be seen for the final (A1) to be awarded.
\({\text{V}}{{\text{O}}^2} + {115^2} = {186^2}\) OR \(\sqrt {{{186}^2} – {{115}^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras formula. Accept alternative methods.
\({\text{(VO}} = )\,\,146\,({\text{m}})\,\,(146.188…)\) (A1)(G2)
Note: Use of full calculator display for \({\text{VM}}\) gives \(146.443…\,{\text{(m)}}\).
Units are required in part (c)
\(\frac{1}{3}({230^2} \times 146.188…)\) (M1)
Note: Award (M1) for correct substitution in volume formula. Follow through from part (b).
\( = 2\,580\,000\,{{\text{m}}^3}\,\,(2\,577\,785…\,{{\text{m}}^3})\) (A1)(ft)(G2)
Note: The answer is \(2\,580\,000\,{{\text{m}}^3}\) , the units are required. Use of \({\text{OV}} = 146.442\) gives \(2582271…\,{{\text{m}}^3}\)
Use of \({\text{OV}} = 146\) gives \(2574466…\,{{\text{m}}^3}.\)
\(2.58 \times {10^6}\,({{\text{m}}^3})\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for \(2.58\) and (A1)(ft) for \( \times {10^6}.\,\)
Award (A0)(A0) for answers of the type: \(2.58 \times {10^5}\,({{\text{m}}^3}).\)
Follow through from part (c).
the volume of a wall would be \(430\,000 \times 5 \times 1\) (M1)
Note: Award (M1) for correct substitution into volume formula.
\(2150000\,({{\text{m}}^3})\) (A1)(G2)
which is less than the volume of the pyramid (R1)(ft)
Ahmad is correct. (A1)(ft)
OR
the length of the wall would be \(\frac{{{\text{their part (c)}}}}{{5 \times 1 \times 1000}}\) (M1)
Note: Award (M1) for dividing their part (c) by \(5000.\)
\(516\,({\text{km}})\) (A1)(ft)(G2)
which is more than the distance from Paris to Amsterdam (R1)(ft)
Ahmad is correct. (A1)(ft)
Note: Do not award final (A1) without an explicit comparison. Follow through from part (c) or part (d). Award (R1) for reasoning that is consistent with their working in part (e); comparing two volumes, or comparing two lengths.
Units are required in part (f)(ii).
i) \({\text{A}}{{\text{W}}^2} = {160^2} + {230^2} – 2 \times 160 \times 230 \times \cos \,(15^\circ )\) (M1)(A1)
Note: Award (M1) for substitution into cosine rule formula, (A1) for correct substitution.
\({\text{AW}} = 86.1\,({\text{m}})\,\,\,(86.0689…)\) (A1)(G2)
Note: Award (M0)(A0)(A0) if \({\text{BAW}}\) or \({\text{AWB}}\) is considered to be a right angled triangle.
ii) \({\text{area}} = \frac{1}{2} \times 230 \times 160 \times \sin \,(15^\circ )\) (M1)(A1)
Note: Award (M1) for substitution into area formula, (A1) for correct substitutions.
\( = 4760\,{{\text{m}}^2}\,\,\,(4762.27…\,{{\text{m}}^2})\) (A1)(G2)
Note: The answer is \(4760\,{{\text{m}}^2}\) , the units are required.
Question
A playground, when viewed from above, is shaped like a quadrilateral, \({\text{ABCD}}\), where \({\text{AB}} = 21.8\,{\text{m}}\) and \({\text{CD}} = 11\,{\text{m}}\) . Three of the internal angles have been measured and angle \({\text{ABC}} = 47^\circ \) , angle \({\text{ACB}} = 63^\circ \) and angle \({\text{CAD}} = 30^\circ \) . This information is represented in the following diagram.
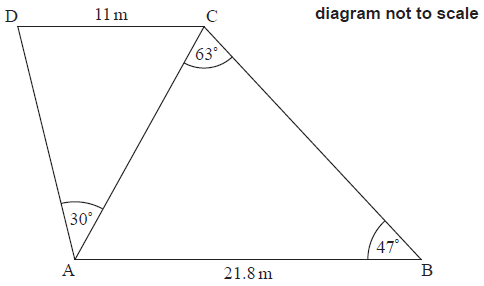
Calculate the distance \({\text{AC}}\).[3]
Calculate angle \({\text{ADC}}\).[3]
There is a tree at \({\text{C}}\), perpendicular to the ground. The angle of elevation to the top of the tree from \({\text{D}}\) is \(35^\circ \).
Calculate the height of the tree.[2]
Chavi estimates that the height of the tree is \(6\,{\text{m}}\).
Calculate the percentage error in Chavi’s estimate.[2]
Chavi is celebrating her birthday with her friends on the playground. Her mother brings a \(2\,\,{\text{litre}}\) bottle of orange juice to share among them. She also brings cone-shaped paper cups.
Each cup has a vertical height of \(10\,{\text{cm}}\) and the top of the cup has a diameter of \(6\,{\text{cm}}\).
Calculate the volume of one paper cup.[3]
Calculate the maximum number of cups that can be completely filled with the \(2\,\,{\text{litre}}\) bottle of orange juice.[3]
Answer/Explanation
Markscheme
\(\frac{{21.8}}{{\sin 63^\circ }} = \frac{{{\text{AC}}}}{{\sin 47^\circ }}\) (M1)(A1)
Note: Award (M1) for substitution into the sine rule formula, (A1) for correct substitution.
\(({\text{AC}} = )\,\,17.9\,({\text{m}})\,\,\,(17.8938…\,({\text{m}}))\) (A1)(G2)
\(\frac{{11}}{{\sin 30}} = \frac{{17.8938…}}{{\sin {\text{ADC}}}}\) (M1)(A1)(ft)
Note: Award (M1) for substitution into the sine rule formula, (A1) for correct substitution.
\(\left( {{\text{Angle ADC}} = } \right)\,\,\,54.4^\circ \,\,\,(54.4250…^\circ )\) (A1)(ft)(G2)
Note: Accept \(54.5\,\,(54.4527…)\) or \(126\,\,(125.547…)\) from using their \(3\) sf answer.
Follow through from part (a). Accept \(125.575…\)
\(11 \times \tan 35^\circ \) (or equivalent) (M1)
Note: Award (M1) for correct substitution into trigonometric ratio.
\(7.70\,({\text{m}})\,\,\,(7.70228…\,({\text{m}}))\) (A1)(G2)
\(\left| {\frac{{6 – 7.70228…}}{{7.70228…}}} \right| \times 100\,\% \) (M1)
Note: Award (M1) for correct substitution into the percentage error formula.
OR
\(100 – \left| {\frac{{6 \times 100}}{{7.70228…}}} \right|\) (M1)
Note: Award (M1) for the alternative method.
\(22.1\,(\% )\,\,\,(22.1009…\,(\% ))\) (A1)(ft)(G2)
Note: Award at most (M1)(A0) for a final answer that is negative. Follow through from part (c).
\(\frac{1}{3}\pi \times {3^2} \times 10\) (A1)(M1)
Note: Award (A1) for \(3\) seen, (M1) for their correct substitution into volume of a cone formula.
\(94.2\,{\text{c}}{{\text{m}}^3}\,\,\,(30\pi \,{\text{c}}{{\text{m}}^3},\,\,94.2477…\,{\text{c}}{{\text{m}}^3})\) (A1)(G3)
Note: The answer is \(94.2\,{\text{c}}{{\text{m}}^3}\), units are required. Award at most (A0)(M1)(A0) if an incorrect value for \(r\) is used.
\(\frac{{2000}}{{94.2477…}}\) OR \(\frac{2}{{0.0942477…}}\) (M1)(M1)
Note: Award (M1) for correct conversion (litres to \({\text{c}}{{\text{m}}^3}\) or \({\text{c}}{{\text{m}}^3}\) to litres), (M1) for dividing by their part (e) (or their converted part (e)).
\(21\) (A1)(ft)(G2)
Note: The final (A1) is not awarded if the final answer is not an integer. Follow through from part (e), but only if the answer is rounded down.
Question
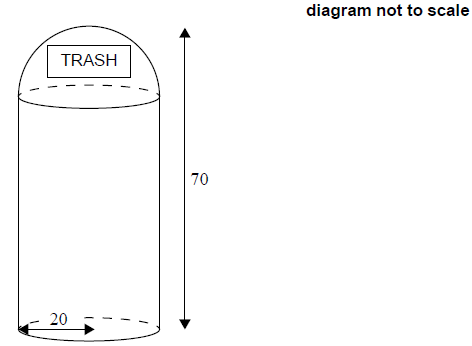
A manufacturer makes trash cans in the form of a cylinder with a hemispherical top. The trash can has a height of 70 cm. The base radius of both the cylinder and the hemispherical top is 20 cm.
A designer is asked to produce a new trash can.
The new trash can will also be in the form of a cylinder with a hemispherical top.
This trash can will have a height of H cm and a base radius of r cm.
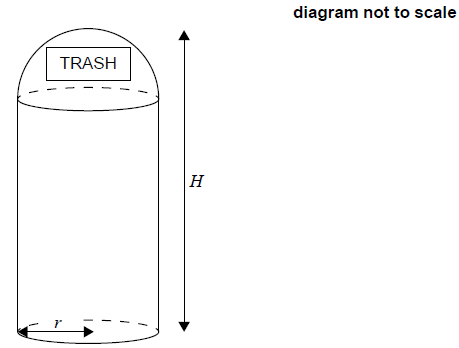
There is a design constraint such that H + 2r = 110 cm.
The designer has to maximize the volume of the trash can.
Write down the height of the cylinder.[1]
Find the total volume of the trash can.[4]
Find the height of the cylinder, h , of the new trash can, in terms of r.[2]
Show that the volume, V cm3 , of the new trash can is given by
\(V = 110\pi {r^3}\).[3]
Using your graphic display calculator, find the value of r which maximizes the value of V.[2]
The designer claims that the new trash can has a capacity that is at least 40% greater than the capacity of the original trash can.
State whether the designer’s claim is correct. Justify your answer.[4]
Answer/Explanation
Markscheme
50 (cm) (A1)[1 mark]
\(\pi \times 50 \times {20^2} + \frac{1}{2} \times \frac{4}{3} \times \pi \times {20^3}\) (M1)(M1)(M1)
Note: Award (M1) for their correctly substituted volume of cylinder, (M1) for correctly substituted volume of sphere formula, (M1) for halving the substituted volume of sphere formula. Award at most (M1)(M1)(M0) if there is no addition of the volumes.
\( = 79600\,\,\left( {{\text{c}}{{\text{m}}^3}} \right)\,\,\left( {79587.0 \ldots \left( {{\text{c}}{{\text{m}}^3}} \right)\,,\,\,\frac{{76000}}{3}\pi } \right)\) (A1)(ft) (G3)
Note: Follow through from part (a).[4 marks]
h = H − r (or equivalent) OR H = 110 − 2r (M1)
Note: Award (M1) for writing h in terms of H and r or for writing H in terms of r.
(h =) 110 − 3r (A1) (G2)[2 marks]
\(\left( {V = } \right)\,\,\,\,\frac{2}{3}\pi {r^3} + \pi {r^2} \times \left( {110 – 3r} \right)\) (M1)(M1)(M1)
Note: Award (M1) for volume of hemisphere, (M1) for correct substitution of their h into the volume of a cylinder, (M1) for addition of two correctly substituted volumes leading to the given answer. Award at most (M1)(M1)(M0) for subsequent working that does not lead to the given answer. Award at most (M1)(M1)(M0) for substituting H = 110 − 2r as their h.
\(V = 110\pi {r^2} – \frac{7}{3}\pi {r^3}\) (AG)[3 marks]
(r =) 31.4 (cm) (31.4285… (cm)) (G2)
OR
\(\left( \pi \right)\left( {220r – 7{r^2}} \right) = 0\) (M1)
Note: Award (M1) for setting the correct derivative equal to zero.
(r =) 31.4 (cm) (31.4285… (cm)) (A1)[2 marks]
\(\left( {V = } \right)\,\,\,\,110\pi {\left( {31.4285 \ldots } \right)^3} – \frac{7}{3}\pi {\left( {31.4285 \ldots } \right)^3}\) (M1)
Note: Award (M1) for correct substitution of their 31.4285… into the given equation.
= 114000 (113781…) (A1)(ft)
Note: Follow through from part (e).
(increase in capacity =) \(\frac{{113.781 \ldots – 79587.0 \ldots }}{{79587.0 \ldots }} \times 100 = 43.0\,\,\left( {\text{% }} \right)\) (R1)(ft)
Note: Award (R1)(ft) for finding the correct percentage increase from their two volumes.
OR
1.4 × 79587.0… = 111421.81… (R1)(ft)
Note: Award (R1)(ft) for finding the capacity of a trash can 40% larger than the original.
Claim is correct (A1)(ft)
Note: Follow through from parts (b), (e) and within part (f). The final (R1)(A1)(ft) can be awarded for their correct reason and conclusion. Do not award (R0)(A1)(ft).[4 marks]
Question
An office block, ABCPQR, is built in the shape of a triangular prism with its “footprint”, ABC, on horizontal ground. \({\text{AB}} = 70{\text{ m}}\), \({\text{BC}} = 50{\text{ m}}\) and \({\text{AC}} = 30{\text{ m}}\). The vertical height of the office block is \(120{\text{ m}}\) .
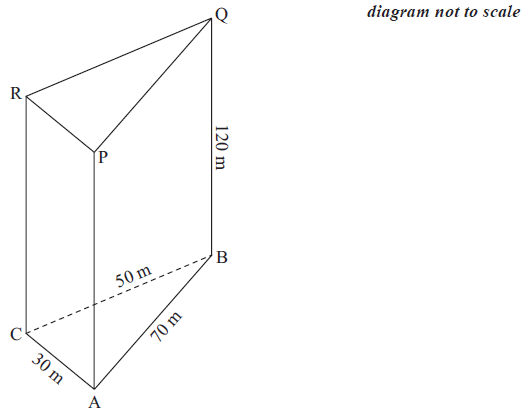
Calculate the size of angle ACB.[3]
Calculate the area of the building’s footprint, ABC.[3]
Calculate the volume of the office block.[2]
To stabilize the structure, a steel beam must be made that runs from point C to point Q.
Calculate the length of CQ.[2]
Calculate the angle CQ makes with BC.
Answer/Explanation
Markscheme
\(\cos {\text{ACB}} = \frac{{{{30}^2} + {{50}^2} – {{70}^2}}}{{2 \times 30 \times 50}}\) (M1)(A1)
Note: Award (M1) for substituted cosine rule formula, (A1) for correct substitution.
\({\text{ACB}} = {120^ \circ }\) (A1)(G2)
\({\text{Area of triangle ABC}} = \frac{{30(50)\sin {{120}^ \circ }}}{2}\) (M1)(A1)(ft)
Note: Award (M1) for substituted area formula, (A1)(ft) for correct substitution.
\( = 650{\text{ }}{{\text{m}}^2}\) \((649.519 \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G2)
Notes: The answer is \(650{\text{ }}{{\text{m}}^2}\) ; the units are required. Follow through from their answer in part (a).
\({\text{Volume}} = 649.519 \ldots \times 120\) (M1)
\( = 77900{\text{ }}{{\text{m}}^3}\) (\(77942.2 \ldots {\text{ }}{{\text{m}}^3}\)) (A1)(G2)
Note: The answer is \(77900{\text{ }}{{\text{m}}^3}\) ; the units are required. Do not penalise lack of units if already penalized in part (b). Accept \(78000{\text{ }}{{\text{m}}^3}\) from use of 3sf answer \(650{\text{ }}{{\text{m}}^2}\) from part (b).
\({\text{C}}{{\text{Q}}^2} = {50^2} + {120^2}\) (M1)
\({\text{CQ}} = 130{\text{ (m)}}\) (A1)(G2)
Note: The units are not required.
\(\tan {\text{QCB}} = \frac{{120}}{{50}}\) (M1)
Note: Award (M1) for correct substituted trig formula.
\({\text{QCB}} = {67.4^ \circ }\) (\(67.3801 \ldots \)) (A1)(G2)
Note: Accept equivalent methods.