Question
The function \(f(x) = 5 – 3({2^{ – x}})\) is defined for \(x \geqslant 0\).
On the axes below sketch the graph of f (x) and show the behaviour of the curve as x increases.[3]
Write down the coordinates of any intercepts with the axes.
[1]
Draw the line y = 5 on your sketch.[1]
Write down the number of solutions to the equation f (x) = 5 .[1]
Answer/Explanation
Markscheme
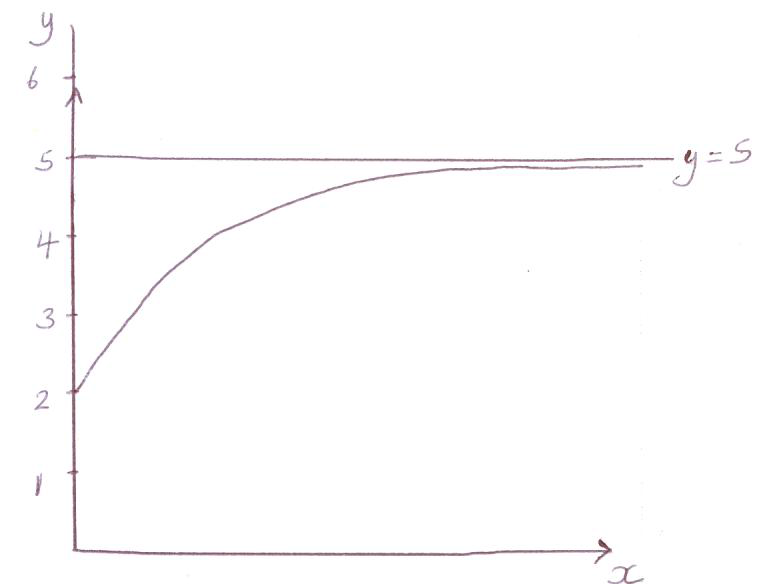(A1)(A1)(A1)
Notes: Award (A1) for labels and scale on y-axis.
Award (A1) for smooth increasing curve in the given domain.
Award (A1) for asymptote implied (\({\text{gradient}} \to {\text{0}}\)).[3 marks]
(0, 2) accept x = 0, y = 2 (A1) (C4)
Note: If incorrect domain used and both (0, 2) and (\( – \)0.737, 0) seen award (A1)(ft).[1 mark]
line passing through (0, 5), parallel to x axis and not intersecting their graph. (A1) (C1)[1 mark]
zero (A1) (C1)[1 mark]
Question
The \(x\)-coordinate of the minimum point of the quadratic function \(f(x) = 2{x^2} + kx + 4\) is \(x =1.25\).
(i) Find the value of \(k\) .
(ii) Calculate the \(y\)-coordinate of this minimum point.[4]
Sketch the graph of \(y = f(x)\) for the domain \( – 1 \leqslant x \leqslant 3\).
[2]
Answer/Explanation
Markscheme
(i) \(1.25 = – \frac{k}{{2(2)}}\) (M1)
OR
\(f'(x) = 4x + k = 0\) (M1)
Note: Award (M1) for setting the gradient function to zero.
\(k = – 5\) (A1) (C2)
(ii) \(2{(1.25)^2} – 5(1.25) + 4\) (M1)
\( = 0.875\) (A1)(ft) (C2)
Note: Follow through from their \(k\).[4 marks]
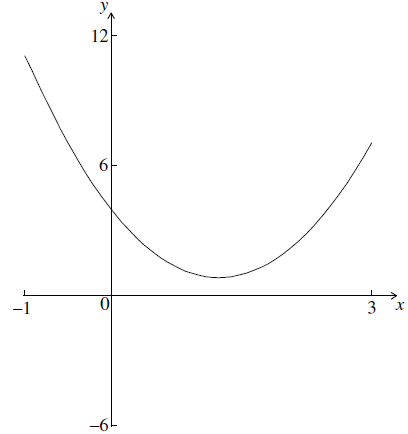(A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for a curve with correct concavity consistent with their \(k\) passing through (0, 4).
(A1)(ft) for minimum in approximately the correct place. Follow through from their part (a).[2 marks]
Question
y = f (x) is a quadratic function. The graph of f (x) intersects the y-axis at the point A(0, 6) and the x-axis at the point B(1, 0). The vertex of the graph is at the point C(2, –2).
Write down the equation of the axis of symmetry.[2]
Sketch the graph of y = f (x) on the axes below for 0 ≤ x ≤ 4 . Mark clearly on the sketch the points A , B , and C.
[3]
The graph of y = f (x) intersects the x-axis for a second time at point D.
Write down the x-coordinate of point D.[1]
Answer/Explanation
Markscheme
x = 2 (A1)(A1) (C2)
Notes: Award (A1)(A0) for “ x = constant” (other than 2). Award (A0)(A1) for y = 2. Award (A0)(A0) for only seeing 2. Award (A0)(A0) for 2 = –b / 2a.[2 marks]
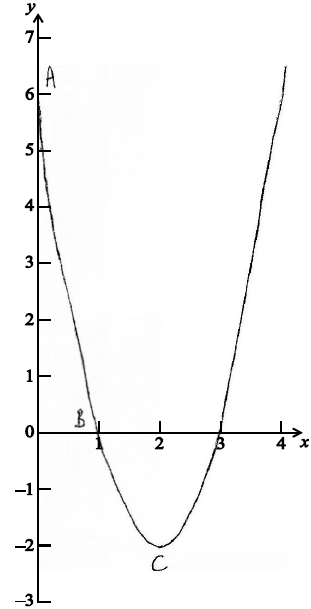
(A1) for correctly plotting and labelling A, B and C
(A1) for a smooth curve passing through the three given points
(A1) for completing the symmetry of the curve over the domain given. (A3) (C3)
Notes: For A marks to be awarded for the curve, each segment must be a reasonable attempt at a continuous curve. If straight line segments are used, penalise once only in the last two marks.[3 marks]
3 (A1)(ft) (C1)
Notes: (A0) for coordinates. Accept x = 3 or D = 3 .[1 mark]
Question
Consider the two functions, \(f\) and \(g\), where
\(f(x) = \frac{5}{{{x^2} + 1}}\)
\(g(x) = {(x – 2)^2}\)
Sketch the graphs of \(y = f(x)\) and \(y = g(x)\) on the axes below. Indicate clearly the points where each graph intersects the y-axis.
[4]Use your graphic display calculator to solve \(f(x) = g(x)\).[2]
Answer/Explanation
Markscheme
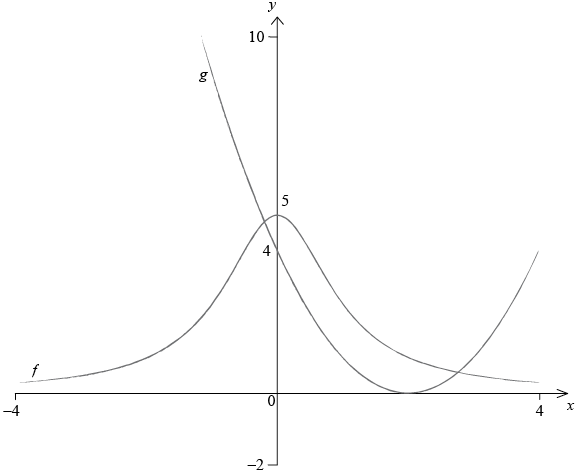
\(f(x)\): a smooth curve symmetrical about y-axis, \(f(x) > 0\) (A1)
Note: If the graph crosses the x-axis award (A0).
Intercept at their numbered \(y = 5\) (A1)
Note: Accept clear scale marks instead of a number.
\(g(x)\): a smooth parabola with axis of symmetry at about \(x = 2\) (the 2 does not need to be numbered) and \(g(x) \geqslant 0\) (A1)
Note: Right hand side must not be higher than the maximum of \(f(x)\) at \(x = 4\).
Accept the quadratic correctly drawn beyond \(x = 4\).
Intercept at their numbered \(y = 4\) (A1) (C4)
Note: Accept clear scale marks instead of a number.[4 marks]
\(–0.195, 2.76\) \((–0.194808…, 2.761377…)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A0)(A1)(ft) if both coordinates are given.
Follow through only if \(f(x) = \frac{5}{{{x^2}}} + 1\) is sketched; the solutions are \(–0.841, 3.22\) \((–0.840913…, 3.217747…)\)[2 marks]
Question
Consider the functions \(f(x) = x + 1\) and \(g(x) = {3^x} – 2\).
Write down
(i) the \(x\)-intercept of the graph of \(y = {\text{ }}f(x)\);
(ii) the \(y\)-intercept of the graph of \(y = {\text{ }}g(x)\).[2]
Solve \(f(x) = g(x)\).[2]
Write down the interval for the values of \(x\) for which \(f(x) > g(x)\).[2]
Answer/Explanation
Markscheme
(i) \(( – 1,{\text{ }}0)\) (A1)
Note: Accept \( – 1\).
(ii) \((0,{\text{ }} – 1)\) (A1) (C2)
Note: Accept \( – 1\).
\((x = ){\text{ }} – 2.96{\text{ }}( – 2.96135 \ldots )\) (A1)
\((x = ){\text{ }}1.34{\text{ }}(1.33508 \ldots )\) (A1) (C2)
\( – 2.96 < x < 1.34\;\;\;{\mathbf{OR}}\;\;\;\left] { – 2.96,{\text{ }}1.34} \right[\;\;\;{\mathbf{OR}}\;\;\;( – 2.96,{\text{ }}1.34)\) (A1)(ft)(A1) (C2)
Notes: Award (A1)(ft) for both correct endpoints of the interval, (A1) for correct strict inequalities (or correct open interval notation).
Follow through from part (b).
Question
The axis of symmetry of the graph of a quadratic function has the equation x \( = – \frac{1}{2}\)
Draw the axis of symmetry on the following axes.
The graph of the quadratic function intersects the x-axis at the point N(2, 0) . There is a second point, M, at which the graph of the quadratic function intersects the x-axis.[1]
Draw the axis of symmetry on the following axes.
[1]
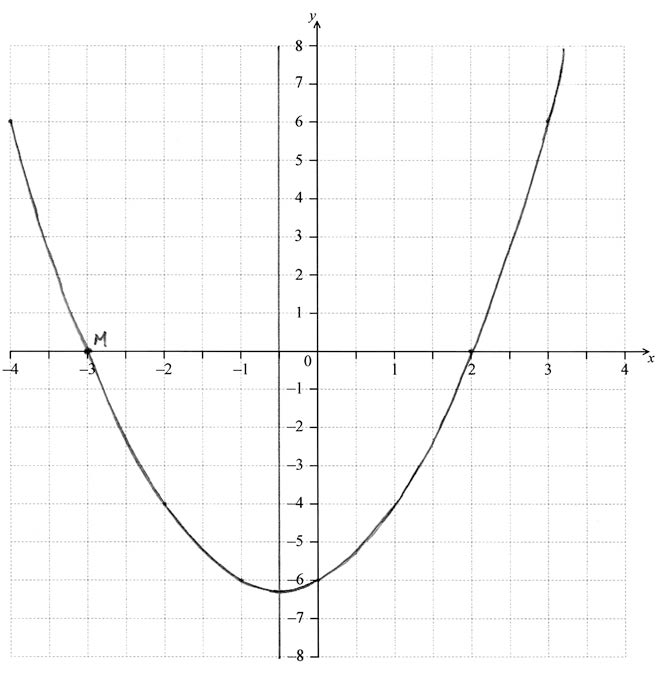
The graph of the quadratic function intersects the \(x\)-axis at the point \({\text{N}}(2, 0)\). There is a second point, \({\text{M}}\), at which the graph of the quadratic function intersects the \(x\)-axis.
Clearly mark and label point \({\text{M}}\) on the axes.[1]
(i) Find the value of \(b\) and the value of \(c\).
(ii) Draw the graph of the function on the axes.[4]
Answer/Explanation
Markscheme
vertical straight line which may be dotted passing through \(\left( { – \frac{1}{2},{\text{ }}0} \right)\) (A1) (C1)
vertical straight line which may be dotted passing through \(\left( { – \frac{1}{2},{\text{ }}0} \right)\) (A1) (C1)
point \({\text{M }}( – 3,{\text{ }}0)\) correctly marked on the \(x\)-axis (A1)(ft) (C1)
Note: Follow through from part (a).
(i) \(b = 1\), \(c = – 6\) (A1)(ft)(A1)(ft)
Notes: Follow through from (b).
(ii) smooth parabola passing through \({\text{M}}\) and \({\text{N}}\) (A1)(ft)
Note: Follow through from their point \({\text{M}}\) from part (b).
parabola passing through \((0,{\text{ }} – 6)\) and symmetrical about \(x = – 0.5\) (A1)(ft) (C4)
Note: Follow through from part (c)(i).
If parabola is not smooth and not concave up award at most (A1)(A0).
Question
Consider the curve \(y = 1 + \frac{1}{{2x}},\,\,x \ne 0.\)
For this curve, write down
i) the value of the \(x\)-intercept;
ii) the equation of the vertical asymptote.[3]
Sketch the curve for \( – 2 \leqslant x \leqslant 4\) on the axes below.
[3]
Answer/Explanation
Markscheme
i) \(\left( {x = } \right) – 0.5\,\,\left( { – \frac{1}{2}} \right)\) (A1)
ii) \(x = 0\) (A1)(A1) (C3)
Note: Award (A1) for “\(x = \)” and (A1) for “\(0\)” seen as part of an equation.
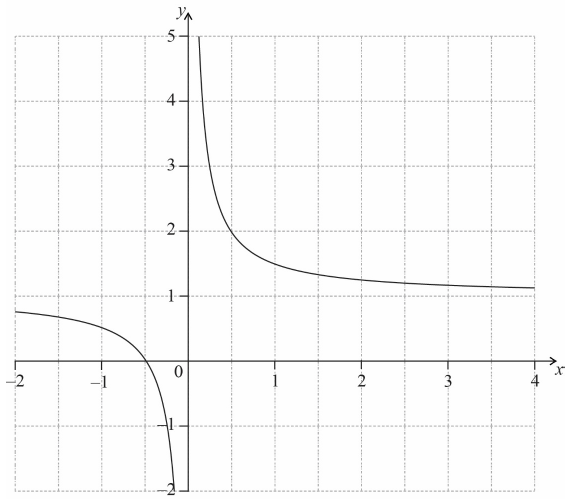
(A1)(ft)(A1)(ft)(A1) (C3)
Note: Award (A1)(ft) for correct \(x\)-intercept, (A1)(ft) for asymptotic behaviour at \(y\)-axis, (A1) for approximately correct shape (cannot intersect the horizontal asymptote of \(y = 1\)). Follow through from part (a).
Question
The function \(f\) is of the form \(f(x) = ax + b + \frac{c}{x}\), where \(a\) , \(b\) and \(c\) are positive integers.
Part of the graph of \(y = f(x)\) is shown on the axes below. The graph of the function has its local maximum at \(( – 2,{\text{ }} – 2)\) and its local minimum at \((2,{\text{ }}6)\).
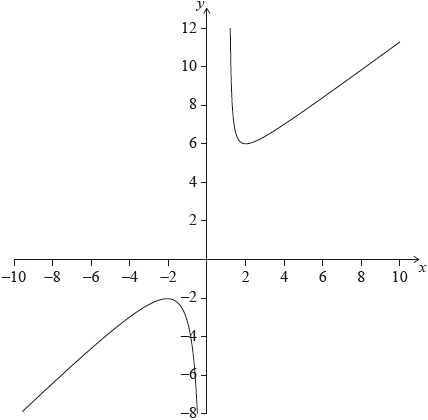
Write down the domain of the function.[2]
Draw the line \(y = – 6\) on the axes.[1]
Write down the number of solutions to \(f(x) = – 6\).[1]
Find the range of values of \(k\) for which \(f(x) = k\) has no solution.[2]
Answer/Explanation
Markscheme
\((x \in \mathbb{R}),{\text{ }}x \ne 0\) (A2) (C2)
Note: Accept equivalent notation. Award (A1)(A0) for \(y \ne 0\).
Award (A1) for a clear statement that demonstrates understanding of the meaning of domain. For example, \({\text{D}}:( – \infty ,{\text{ }}0) \cup (1,{\text{ }}\infty )\) should be awarded (A1)(A0).[2 marks]
(A1) (C1)
Note: The command term “Draw” states: “A ruler (straight edge) should be used for straight lines”; do not accept a freehand \(y = – 6\) line.[1 mark]
2 (A1)(ft) (C1)
Note: Follow through from part (b)(i).[1 mark]
\( – 2 < k < 6\) (A1)(A1) (C2)
Note: Award (A1) for both end points correct and (A1) for correct strict inequalities.
Award at most (A1)(A0) if the stated variable is different from \(k\) or \(y\) for example \( – 2 < x < 6\) is (A1)(A0).[2 marks]
Question
The diagram shows part of the graph of a function \(y = f(x)\). The graph passes through point \({\text{A}}(1,{\text{ }}3)\).
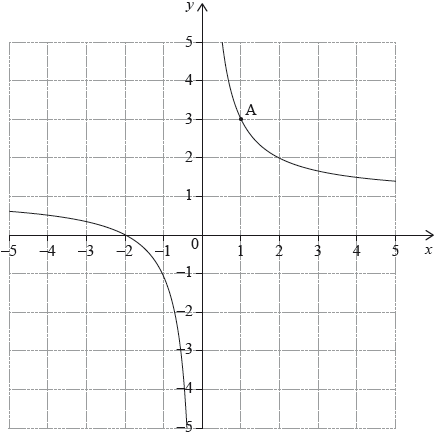
The tangent to the graph of \(y = f(x)\) at A has equation \(y = – 2x + 5\). Let \(N\) be the normal to the graph of \(y = f(x)\) at A.
Write down the value of \(f(1)\).[1]
Find the equation of \(N\). Give your answer in the form \(ax + by + d = 0\) where \(a\), \(b\), \(d \in \mathbb{Z}\).[3]
Draw the line \(N\) on the diagram above.[2]
Answer/Explanation
Markscheme
3 (A1) (C1)
Notes: Accept \(y = 3\)[1 mark]
\(3 = 0.5(1) + c\)\(\,\,\,\)OR\(\,\,\,\)\(y – 3 = 0.5(x – 1)\) (A1)(A1)
Note: Award (A1) for correct gradient, (A1) for correct substitution of \({\text{A}}(1,{\text{ }}3)\) in the equation of line.
\(x – 2y + 5 = 0\) or any integer multiple (A1)(ft) (C3)
Note: Award (A1)(ft) for their equation correctly rearranged in the indicated form.
The candidate’s answer must be an equation for this mark.[3 marks]
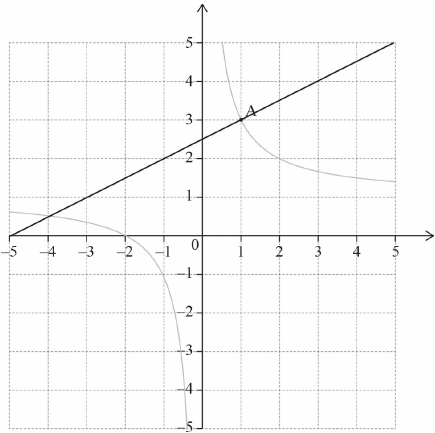(M1)(A1)(ft) (C2)
Note: Award M1) for a straight line, with positive gradient, passing through \((1,{\text{ }}3)\), (A1)(ft) for line (or extension of their line) passing approximately through 2.5 or their intercept with the \(y\)-axis.[2 marks]
Question
Consider the graph of the function \(y = f(x)\) defined below.
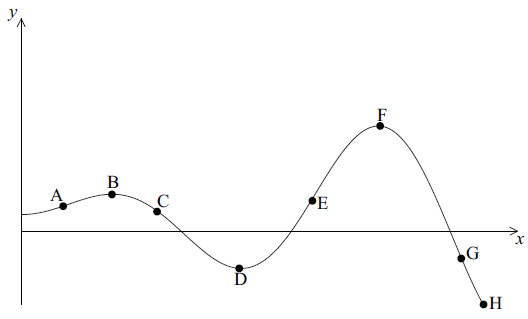
Write down all the labelled points on the curve
that are local maximum points;[1]
where the function attains its least value;[1]
where the function attains its greatest value;[1]
where the gradient of the tangent to the curve is positive;[1]
where \(f(x) > 0\) and \(f'(x) < 0\) .[2]
Answer/Explanation
Markscheme
B, F (C1)
H (C1)
F (C1)
A, E (C1)
C (C2)
Question
On the grid below sketch the graph of the function \(f(x) = 2{(1.6)^x}\) for the domain \(0 \leqslant x \leqslant 3\) .
[2]
Write down the coordinates of the \(y\)-intercept of the graph of \(y = f(x)\) .[1]
On the grid draw the graph of the function \(g(x) = 5 – 2x\) for the domain \(0 \leqslant x \leqslant 3\).[2]
Use your graphic display calculator to solve \(f(x) = g(x)\) .[1]
Answer/Explanation
Markscheme
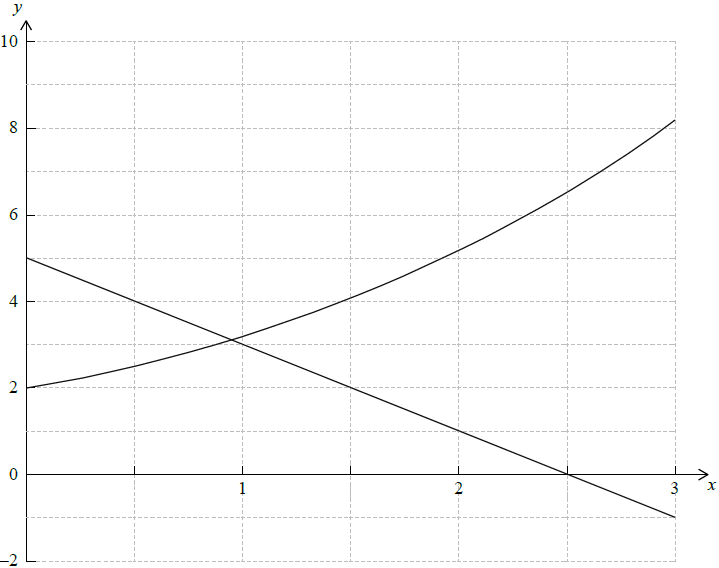
Note: Award (A1) correct endpoints, (A1) for smooth curve. (A1)(A1) (C2)
\((0{\text{, }}2)\) (A1) (C1)
Note: Accept \(x = 0\), \(y = 2\)
Straight line in the given domain (A1)
Axes intercepts in the correct positions (A1) (C2)
\(x = 0.943\) (\(0.94259 \ldots \)) (A1) (C1)
Note: Award (A0) if \(y\)-coordinate given.