Question
[without GDC]
The random variable \(X\) follows the binomial distribution B(\(n,p\)). Given that \(E(X)\) = \(10\) and Var(\(X\)) = \(6\) find the values of \(n\) and \(p\).
Answer/Explanation
Ans
\(np=10\) and \(np(1-p)=6\). Hence \(10(1-p)=6 \Leftrightarrow \(p=0.4\) and \(n=25\)
Question
[without GDC]
The random variable \(X\) follows the binomial distribution B(\(n,p\)). Given that \(E(X)\) = \(10\) and Var(\(X\)) = \(6\) find the values of \(n\) and \(p\).
Answer/Explanation
Ans
\(np=10\) and \(np(1-p)=6\). Hence \(10(1-p)=6 \Leftrightarrow \(p=0.4\) and \(n=25\)
Question
[without GDC]
Two fair four-sided dice, one red and one green, are thrown. For each die, the faces are labelled 1, 2, 3, 4. The score for each die is the number which lands face down.
The sample space is shown below:
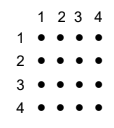
(a) Write down the probability that two scores of \(4\) are obtained.
Let \(X\) be the number of \(4\)s that land face down.
(b) Complete the following probability distribution for \(X\).

(c) Find \(E(X)\).
Chris plays a game where he rolls the dice above. If two \(4\)s are obtained he wins \(20\)€.
If only one \(4\) is obtained he wins \(5\)€. If no \(4\) is obtained he loses \(2\)€
(d) Find the expected amount earned in one game.
(e) If Chris plays this game \(100\) times find the amount he is expected to win.
Answer/Explanation
Ans
(a) Probability of two \(4\)s is \(\frac{1}{16}(=0.0625)\)
(b) 
(c) \(E(X)=\sum_{0}^{2} xP(X=x),=0\times \frac{9}{16}+1\times \frac{6}{16}+2\times \frac{1}{16}\frac{8}{16}\left ( =\frac{1}{2} \right )\)
or \(E(X)=np=2\times \frac{1}{4}=\frac{1}{2}\)
(d) 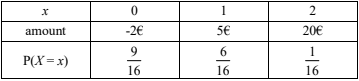
Expected amount = \(-2\times \frac{9}{16}+5\times \frac{6}{16}+20\times \frac{1}{16}= 2\)€
(e) \(100\times 2\)= \(200\) €