Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = {x^3} – 4x + 1\) .
Expand \({(x + h)^3}\) .
Use the formula \(f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) – f(x)}}{h}\) to show that the derivative of \(f(x)\) is \(3{x^2} – 4\) .
The tangent to the curve of f at the point \({\text{P}}(1{\text{, }} – 2)\) is parallel to the tangent at a point Q. Find the coordinates of Q.
The graph of f is decreasing for \(p < x < q\) . Find the value of p and of q.
Write down the range of values for the gradient of \(f\) .
Answer/Explanation
Markscheme
attempt to expand (M1)
\({(x + h)^3} = {x^3} + 3{x^2}h + 3x{h^2} + {h^3}\) A1 N2
[2 marks]
evidence of substituting \(x + h\) (M1)
correct substitution A1
e.g. \(f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{{{(x + h)}^3} – 4(x + h) + 1 – ({x^3} – 4x + 1)}}{h}\)
simplifying A1
e.g. \(\frac{{({x^3} + 3{x^2}h + 3x{h^2} + {h^3} – 4x – 4h + 1 – {x^3} + 4x – 1)}}{h}\)
factoring out h A1
e.g. \(\frac{{h(3{x^2} + 3xh + {h^2} – 4)}}{h}\)
\(f'(x) = 3{x^2} – 4\) AG N0
[4 marks]
\(f'(1) = – 1\) (A1)
setting up an appropriate equation M1
e.g. \(3{x^2} – 4 = – 1\)
at Q, \(x = – 1,y = 4\) (Q is \(( – 1{\text{, }}4)\)) A1 A1
[4 marks]
recognizing that f is decreasing when \(f'(x) < 0\) R1
correct values for p and q (but do not accept \(p = 1.15{\text{, }}q = – 1.15\) ) A1A1 N1N1
e.g. \(p = – 1.15{\text{, }}q = 1.15\) ; \( \pm \frac{2}{{\sqrt 3 }}\) ; an interval such as \( – 1.15 \le x \le 1.15\)
[3 marks]
\(f'(x) \ge – 4\) , \(y \ge – 4\) , \(\left[ { – 4,\infty } \right[\) A2 N2
[2 marks]
Question
Let \(f(x) = \frac{{100}}{{(1 + 50{{\rm{e}}^{ – 0.2x}})}}\) . Part of the graph of \(f\) is shown below.
Write down \(f(0)\) .
Solve \(f(x) = 95\) .
Find the range of \(f\) .
Show that \(f'(x) = \frac{{1000{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) .
Find the maximum rate of change of \(f\) .
Answer/Explanation
Markscheme
\(f(0) = \frac{{100}}{{51}}\) (exact), \(1.96\) A1 N1
[1 mark]
setting up equation (M1)
eg \(95 = \frac{{100}}{{1 + 50{{\rm{e}}^{ – 0.2x}}}}\) , sketch of graph with horizontal line at \(y = 95\)
\(x = 34.3\) A1 N2
[2 marks]
upper bound of \(y\) is \(100\) (A1)
lower bound of \(y\) is \(0\) (A1)
range is \(0 < y < 100\) A1 N3
[3 marks]
METHOD 1
setting function ready to apply the chain rule (M1)
eg \(100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 1}}\)
evidence of correct differentiation (must be substituted into chain rule) (A1)(A1)
eg \(u’ = – 100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}\) , \(v’ = (50{{\rm{e}}^{ – 0.2x}})( – 0.2)\)
correct chain rule derivative A1
eg \(f'(x) = – 100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}(50{{\rm{e}}^{ – 0.2x}})( – 0.2)\)
correct working clearly leading to the required answer A1
eg \(f'(x) = 1000{{\rm{e}}^{ – 0.2x}}{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}\)
\(f'(x) = \frac{{1000{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) AG N0
METHOD 2
attempt to apply the quotient rule (accept reversed numerator terms) (M1)
eg \(\frac{{vu’ – uv’}}{{{v^2}}}\) , \(\frac{{uv’ – vu’}}{{{v^2}}}\)
evidence of correct differentiation inside the quotient rule (A1)(A1)
eg \(f'(x) = \frac{{(1 + 50{{\rm{e}}^{ – 0.2x}})(0) – 100(50{{\rm{e}}^{ – 0.2x}} \times – 0.2)}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) , \(\frac{{100( – 10){{\rm{e}}^{ – 0.2x}} – 0}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
any correct expression for derivative (\(0\) may not be explicitly seen) (A1)
eg \(\frac{{ – 100(50{{\rm{e}}^{ – 0.2x}} \times – 0.2)}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
correct working clearly leading to the required answer A1
eg \(f'(x) = \frac{{0 – 100( – 10){{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) , \(\frac{{ – 100( – 10){{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
\(f'(x) = \frac{{{\rm{1000}}{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) AG N0
[5 marks]
METHOD 1
sketch of \(f'(x)\) (A1)
eg
recognizing maximum on \(f'(x)\) (M1)
eg dot on max of sketch
finding maximum on graph of \(f'(x)\) A1
eg (\(19.6\), \(5\)) , \(x = 19.560 \ldots \)
maximum rate of increase is \(5\) A1 N2
METHOD 2
recognizing \(f”(x) = 0\) (M1)
finding any correct expression for \(f”(x) = 0\) (A1)
eg \(\frac{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}( – 200{{\rm{e}}^{ – 0.2x}}) – (1000{{\rm{e}}^{ – 0.2x}})(2(1 + 50{{\rm{e}}^{ – 0.2x}})( – 10{{\rm{e}}^{ – 0.2x}}))}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^4}}}\)
finding \(x = 19.560 \ldots \) A1
maximum rate of increase is \(5\) A1 N2
[4 marks]
Question
Let \(f(x) = {x^2} + 2x + 1\) and \(g(x) = x – 5\), for \(x \in \mathbb{R}\).
Find \(f(8)\).
Find \((g \circ f)(x)\).
Solve \((g \circ f)(x) = 0\).
Answer/Explanation
Markscheme
attempt to substitute \(x = 8\) (M1)
eg\(\,\,\,\,\,\)\({8^2} + 2 \times 8 + 1\)
\(f(8) = 81\) A1 N2
[2 marks]
attempt to form composition (in any order) (M1)
eg\(\,\,\,\,\,\)\(f(x – 5),{\text{ }}g\left( {f(x)} \right),{\text{ }}\left( {{x^2} + 2x + 1} \right) – 5\)
\((g \circ f)(x) = {x^2} + 2x – 4\) A1 N2
[2 marks]
valid approach (M1)
eg \(x = \frac{{ – 2 \pm \sqrt {20} }}{2}\),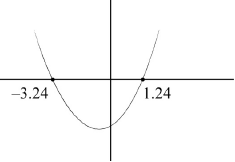 
\(1.23606,{\text{ }} – 3.23606\)
\(x = 1.24,{\text{ }}x = – 3.24\) A1A1 N3
[3 marks]
Question
The following diagram shows the graph of a function \(y = f(x)\), for \( – 6 \leqslant x \leqslant – 2\).
The points \(( – 6,{\text{ }}6)\) and \(( – 2,{\text{ }}6)\) lie on the graph of \(f\). There is a minimum point at \(( – 4,{\text{ }}0)\).
Let \(g(x) = f(x – 5)\).
Write down the range of \(f\).
On the grid above, sketch the graph of \(g\).
Write down the domain of \(g\).
Answer/Explanation
Markscheme
correct interval A2 N2
eg\(\,\,\,\,\,\)\(0 \leqslant y \leqslant 6,{\text{ }}[0,{\text{ }}6]\), from 0 to 6
[2 marks]
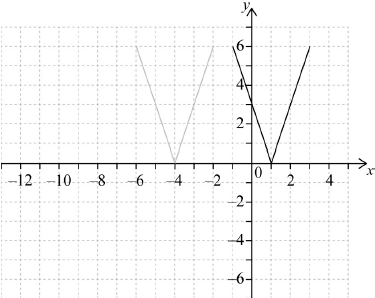M1A1 N2
Note: Award M1 for a horizontal shift of the whole shape, 5 units to the left or right and A1 for the correct graph.
[2 marks]
correct interval A2 N2
eg\(\,\,\,\,\,\)\( – 1 \leqslant x \leqslant 3,{\text{ }}[ – 1,{\text{ }}3]\), from \( – 1\) to 3
[2 marks]
Question
A rock falls off the top of a cliff. Let \(h\) be its height above ground in metres, after \(t\) seconds.
The table below gives values of \(h\) and \(t\) .
Jane thinks that the function \(f(t) = – 0.25{t^3} – 2.32{t^2} + 1.93t + 106\) is a suitable model for the data. Use Jane’s model to
(i) write down the height of the cliff;
(ii) find the height of the rock after 4.5 seconds;
(iii) find after how many seconds the height of the rock is \(30{\text{ m}}\).
Kevin thinks that the function \(g(t) = – 5.2{t^2} + 9.5t + 100\) is a better model for the data. Use Kevin’s model to find when the rock hits the ground.
(i) On graph paper, using a scale of 1 cm to 1 second, and 1 cm to 10 m, plot the data given in the table.
(ii) By comparing the graphs of f and g with the plotted data, explain which function is a better model for the height of the falling rock.
Answer/Explanation
Markscheme
(i) \(106{\text{ m}}\) A1 N1
(ii) substitute \(t = 4.5\) M1
\(h = 44.9{\text{ m}}\) A1 N2
(iii) set up suitable equation M1
e.g. \(f(t) = 30\)
\(t = 4.91\) A1 N1
[5 marks]
recognizing that height is 0 A1
set up suitable equation M1
e.g. \(g(t) = 0\)
\(t = 5.39{\text{ secs}}\) A1 N2
[3 marks]
A1A2 N3
Note: Award A1 for correct scales on axes, A2 for 5 correct points, A1 for 3 or 4 correct points.
(ii) Jane’s function, with 2 valid reasons A1R1R1 N3
e.g. Jane’s passes very close to all the points, Kevin’s has the rock clearly going up initially – not possible if rock falls
Note: Although Jane’s also goes up initially, it only goes up very slightly, and so is the better model.
[6 marks]