Question: [Maximum mark: 20]
Consider the function f (x) = \(\sqrt{x^{2}-1}\), where 1 ≤ x ≤ 2.
(a) Sketch the curve y = f (x), clearly indicating the coordinates of the endpoints.
(b) (i) Show that the inverse function of f is given by f-1(x) = \(\sqrt{x^{2}+1}\).
(ii) State the domain and range of f -1.
The curve y = f (x) is rotated 2π about the y-axis to form a solid of revolution that is used to model a water container.
(c) (i) Show that the volume, Vm3, of water in the container when it is filled to a height of h metres is given by V = \(\pi \left ( \frac{1}{3}h^{3}+h \right )\).
(ii) Hence, determine the maximum volume of the container.
At t = 0, the container is empty. Water is then added to the container at a constant rate of 0.4m3 s-1.
(d) Find the time it takes to fill the container to its maximum volume.
(e) Find the rate of change of the height of the water when the container is filled to half its maximum volume.
Answer/Explanation
Ans:
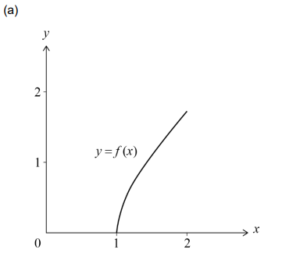
correct shape (concave down) within the given domain 1≤ x ≤ 2
(1, 0) and \(\left ( 2, \sqrt{3} \right )\) (=(2, 1.73))
Note: The coordinates of endpoints may be seen on the graph or marked on the axes.




Question: [Maximum mark: 20]
A function f is defined by \(f(x) = \frac{1}{x^{2}-2x-3},\) where x ∈ R, x ≠ -1, x ≠ 3 .
(a) Sketch the curve y = f (x), clearly indicating any asymptotes with their equations. State the coordinates of any local maximum or minimum points and any points of intersection with the coordinate axes.
A function g is defined by \(g(x) = \frac{1}{x^{2}-2x-3},\) where x ∈ R, x >3.
(b) The inverse of g is g-1.
(i) Show that \(g^{-1}(x)=1+\frac{\sqrt{4x^{2}+x}}{x}.\)
(ii) State the domain of g-1.
A function h is defined by h(x) = arctan \(\frac{x}{2}\), where x ∈ R.
(c) Given that (h º g) (a) = \(\frac{\pi }{4},\) find the value of a.
Give your answer in the form \(p + \frac{q}{2}\sqrt{r},\) where p, q, r ∈ Z+ .
Answer/Explanation
Ans:
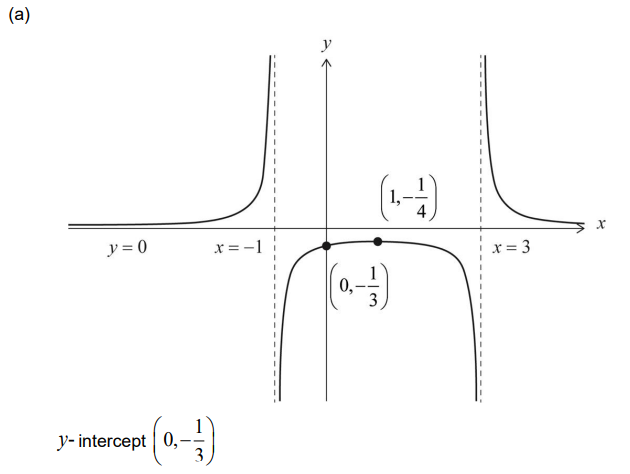
Note: Accept an indication of \(-\frac{1}{3} on the y-axis.\)
vertical asymptotes x =−1 and x = 3
horizontal asymptote y = 0
uses a valid method to find the x-coordinate of the local maximum point
Note: For example, uses the axis of symmetry or attempts to solve f’ (x) = 0 .
local maximum point \(\left ( 1,-\frac{1}{4} \right )\)
Note: Award (M1)A0 for a local maximum point at x =1 and coordinates not given.
three correct branches with correct asymptotic behaviour and the key features in approximately correct relative positions to each other

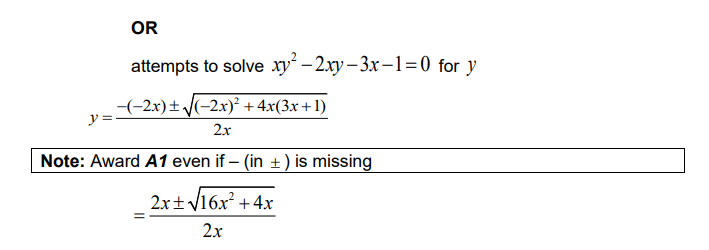



Question
The functions f and g are defined as:
\[f(x) = {{\text{e}}^{{x^2}}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{1}{{x + 3}},{\text{ }}x \ne – 3.\]
(a) Find \(h(x){\text{ where }}h(x) = g \circ f(x)\) .
(b) State the domain of \({h^{ – 1}}(x)\) .
(c) Find \({h^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
(a) \(h(x) = g \circ f(x) = \frac{1}{{{{\text{e}}^{{x^2}}} + 3}},{\text{ }}(x \geqslant 0)\) (M1)A1
(b) \(0 < x \leqslant \frac{1}{4}\) A1A1
Note: Award A1 for limits and A1 for correct inequality signs.
(c) \(y = \frac{1}{{{{\text{e}}^{{x^2}}} + 3}}\)
\(y{{\text{e}}^{{x^2}}} + 3y = 1\) M1
\({{\text{e}}^{{x^2}}} = \frac{{1 – 3y}}{y}\) A1
\({x^2} = \ln \frac{{1 – 3y}}{y}\) M1
\(x = \pm \sqrt {\ln \frac{{1 – 3y}}{y}} \)
\( \Rightarrow {h^{ – 1}}(x) = \sqrt {\ln \frac{{1 – 3x}}{x}} {\text{ }}\left( { = \sqrt {\ln \left( {\frac{1}{x} – 3} \right)} } \right)\) A1
[8 marks]
Question
Let \(f(x) = \frac{4}{{x + 2}},{\text{ }}x \ne – 2{\text{ and }}g(x) = x – 1\).
If \(h = g \circ f\) , find
(a) h(x) ;
(b) \({h^{ – 1}}(x)\) , where \({h^{ – 1}}\) is the inverse of h.
Answer/Explanation
Markscheme
(a) \(h(x) = g\left( {\frac{4}{{x + 2}}} \right)\) (M1)
\( = \frac{4}{{x + 2}} – 1\,\,\,\,\,\left( { = \frac{{2 – x}}{{2 + x}}} \right)\) A1
(b) METHOD 1
\(x = \frac{4}{{y + 2}} – 1\,\,\,\,\,\)(interchanging x and y) M1
Attempting to solve for y M1
\((y + 2)(x + 1) = 4\,\,\,\,\,\left( {y + 2 = \frac{4}{{x + 1}}} \right)\) (A1)
\({h^{ – 1}}(x) = \frac{4}{{x + 1}} – 2\,\,\,\,\,(x \ne – 1)\) A1 N1
METHOD 2
\(x = \frac{{2 – y}}{{2 + y}}\,\,\,\,\,\)(interchanging x and y) M1
Attempting to solve for y M1
\(xy + y = 2 – 2x\,\,\,\,\,\left( {y(x + 1) = 2(1 – x)} \right)\) (A1)
\({h^{ – 1}}(x) = \frac{{2(1 – x)}}{{x + 1}}\,\,\,\,\,(x \ne – 1)\) A1 N1
Note: In either METHOD 1 or METHOD 2 rearranging first and interchanging afterwards is equally acceptable.
[6 marks]
Question
Consider the function f , where \(f(x) = \arcsin (\ln x)\).
(a) Find the domain of f .
(b) Find \({f^{ – 1}}(x)\).
Answer/Explanation
Markscheme
(a) \( – 1 \leqslant \ln x \leqslant 1\) (M1)
\( \Rightarrow \frac{1}{{\text{e}}} \leqslant x \leqslant {\text{e}}\) A1A1
(b) \(y = \arcsin (\ln x) \Rightarrow \ln x = \sin y\) (M1)
\(\ln y = \sin x \Rightarrow y = {{\text{e}}^{\sin x}}\) (M1)
\( \Rightarrow {f^{ – 1}}(x) = {{\text{e}}^{\sin x}}\) A1
[6 marks]
Question
A function f is defined by \(f(x) = \frac{{2x – 3}}{{x – 1}},{\text{ }}x \ne 1\).
(a) Find an expression for \({f^{ – 1}}(x)\).
(b) Solve the equation \(\left| {{f^{ – 1}}(x)} \right| = 1 + {f^{ – 1}}(x)\).
Answer/Explanation
Markscheme
(a) Note: Interchange of variables may take place at any stage.
for the inverse, solve for x in
\(y = \frac{{2x – 3}}{{x – 1}}\)
\(y(x – 1) = 2x – 3\) M1
\(yx – 2x = y – 3\)
\(x(y – 2) = y – 3\) (A1)
\(x = \frac{{y – 3}}{{y – 2}}\)
\( \Rightarrow {f^{ – 1}}(x) = \frac{{x – 3}}{{x – 2}}\,\,\,\,\,(x \ne 2)\) A1
Note: Do not award final A1 unless written in the form \({f^{ – 1}}(x) = \ldots \)
(b) \( \pm {f^{ – 1}}(x) = 1 + {f^{ – 1}}(x)\) leads to
\(2\frac{{x – 3}}{{x – 2}} = – 1\) (M1)
\(x = \frac{8}{3}\) A1
[6 marks]
Question
Consider the function \(f:x \to \sqrt {\frac{\pi }{4} – \arccos x} \).
(a) Find the largest possible domain of f.
(b) Determine an expression for the inverse function, \({f^{ – 1}}\), and write down its domain.
Answer/Explanation
Markscheme
(a) \(\frac{\pi }{4} – \arccos x \geqslant 0\)
\(\arccos x \leqslant \frac{\pi }{4}\) (M1)
\(x \geqslant \frac{{\sqrt 2 }}{2}\,\,\,\,\,\left( {{\text{accept }}x \geqslant \frac{1}{{\sqrt 2 }}} \right)\) (A1)
since \( – 1 \leqslant x \leqslant 1\) (M1)
\( \Rightarrow \frac{{\sqrt 2 }}{2} \leqslant x \leqslant 1\,\,\,\,\,\left( {{\text{accept }}\frac{1}{{\sqrt 2 }} \leqslant x \leqslant 1} \right)\) A1
Note: Penalize the use of \( < \) instead of \( \leqslant \) only once.
(b) \(y = \sqrt {\frac{\pi }{4} – \arccos x} \Rightarrow x = \cos \left( {\frac{\pi }{4} – {y^2}} \right)\) M1A1
\({f^{ – 1}}:x \to \cos \left( {\frac{\pi }{4} – {x^2}} \right)\) A1
\(0 \leqslant x \leqslant \sqrt {\frac{\pi }{4}} \) A1
[8 marks]
