Section B
[Maximum mark: 20]
Question:
Consider the function f (x) = \(\sqrt{x^{2}-1}\), where 1 ≤ x ≤ 2.
(a) Sketch the curve y = f (x), clearly indicating the coordinates of the endpoints.
▶️Answer/Explanation
Ans: 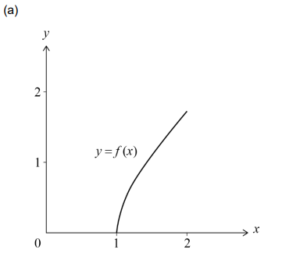
correct shape (concave down) within the given domain 1≤ x ≤ 2
(1, 0) and \(\left ( 2, \sqrt{3} \right )\) (=(2, 1.73))
Note: The coordinates of endpoints may be seen on the graph or marked on the axes.
(b) (i) Show that the inverse function of f is given by f-1(x) = \(\sqrt{x^{2}+1}\).
(ii) State the domain and range of f -1.
The curve y = f (x) is rotated 2π about the y-axis to form a solid of revolution that is used to model a water container.
▶️Answer/Explanation
Ans: 
(c) (i) Show that the volume, Vm3, of water in the container when it is filled to a height of h metres is given by V = \(\pi \left ( \frac{1}{3}h^{3}+h \right )\).
(ii) Hence, determine the maximum volume of the container.
At t = 0, the container is empty. Water is then added to the container at a constant rate of 0.4m3 s-1.
▶️Answer/Explanation
Ans: 
(d) Find the time it takes to fill the container to its maximum volume.
▶️Answer/Explanation
Ans: 
(e) Find the rate of change of the height of the water when the container is filled to half its maximum volume.
▶️Answer/Explanation
Ans: 
[Maximum mark: 8]
Question:
A function f is defined by f(x) = \(\frac{2x – 1}{x + 1}\), where x ∈ R, x ≠ -1.
(a) The graph of y = f (x) has a vertical asymptote and a horizontal asymptote.
Write down the equation of
(i) the vertical asymptote;
(ii) the horizontal asymptote.
▶️Answer/Explanation
Ans: (i) x =−1
(ii) y = 2
(b) On the set of axes below, sketch the graph of y = f (x) .
On your sketch, clearly indicate the asymptotes and the position of any points of intersection with the axes.
▶️Answer/Explanation
Ans: 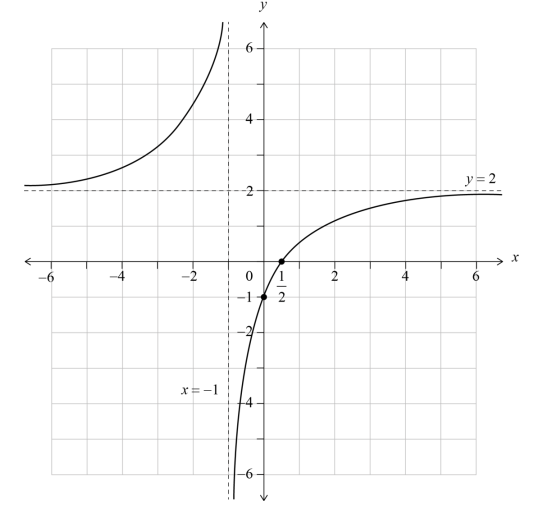
rational function shape with two branches in opposite quadrants, with two correctly positioned asymptotes and asymptotic behaviour shown axes intercepts clearly shown at \(x = \frac{1}{2} and y = -1\)
(c) Hence, solve the inequality \(0<\frac{2x – 1}{x + 1} <2.\)
▶️Answer/Explanation
Ans: x > \(\frac{1}{2}\)
Note: Accept correct alternative correct notation, such as \(\left ( \frac{1}{2}, \infty \right ) and ]\frac{1}{2}, \infty [.\)
(d) Solve the inequality \(0<\frac{2|x|-1}{|x| + 1} <2.\)
▶️Answer/Explanation
Ans: EITHER
attempts to sketch \(y = \frac{2|x| – 1}{|x|+1}\)
OR
attempts to solve 2|x| – 1 = 0
Note: Award the (M1) if \(x = \frac{1}{2} and x = -\frac{1}{2}\) are identified.
THEN
\(x <-\frac{1}{2} and x >\frac{1}{2}\)
Note: Accept the use of a comma. Condone the use of ‘and’. Accept correct alternative notation.
[Maximum mark: 20]
Question:
A function f is defined by \(f(x) = \frac{1}{x^{2}-2x-3},\) where x ∈ R, x ≠ -1, x ≠ 3 .
(a) Sketch the curve y = f (x), clearly indicating any asymptotes with their equations. State the coordinates of any local maximum or minimum points and any points of intersection with the coordinate axes. A function g is defined by \(g(x) = \frac{1}{x^{2}-2x-3},\) where x ∈ R, x >3.
▶️Answer/Explanation
Ans: 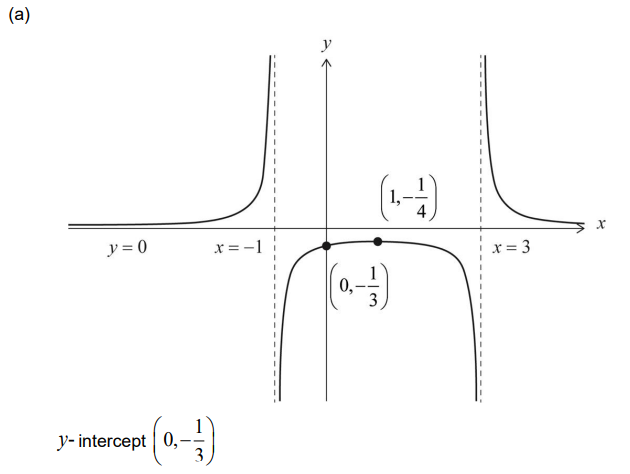
Note: Accept an indication of \(-\frac{1}{3} on the y-axis.\)
vertical asymptotes x =−1 and x = 3
horizontal asymptote y = 0
uses a valid method to find the x-coordinate of the local maximum point
Note: For example, uses the axis of symmetry or attempts to solve f’ (x) = 0 .
local maximum point \(\left ( 1,-\frac{1}{4} \right )\)
Note: Award (M1)A0 for a local maximum point at x =1 and coordinates not given.
three correct branches with correct asymptotic behaviour and the key features in approximately correct relative positions to each other
(b) The inverse of g is g-1.
(i) Show that \(g^{-1}(x)=1+\frac{\sqrt{4x^{2}+x}}{x}.\)
(ii) State the domain of g-1.
A function h is defined by h(x) = arctan \(\frac{x}{2}\), where x ∈ R.
▶️Answer/Explanation
Ans: 
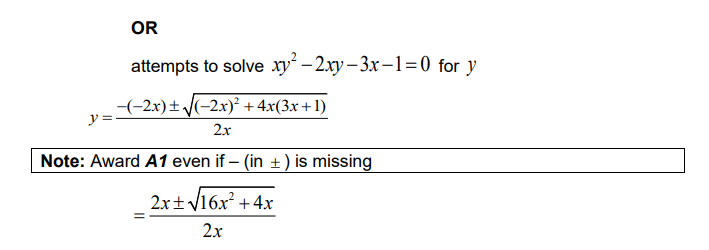

(c) Given that (h º g) (a) = \(\frac{\pi }{4},\) find the value of a.
Give your answer in the form \(p + \frac{q}{2}\sqrt{r},\) where p, q, r ∈ Z+ .
▶️Answer/Explanation
Ans: 

Question
A function is defined as \(f(x) = k\sqrt x \), with \(k > 0\) and \(x \geqslant 0\) .
(a) Sketch the graph of \(y = f(x)\) .
▶️Answer/Explanation
Ans: 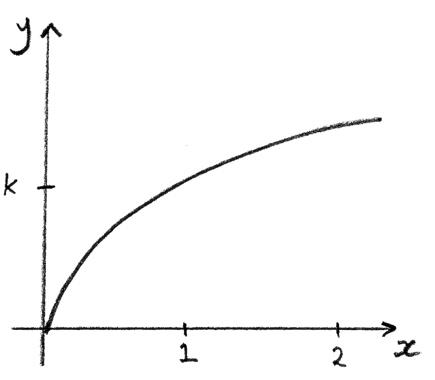
A1
Note: Award A1 for correct concavity, passing through (0, 0) and increasing.
Scales need not be there.
[1 mark]
▶️Answer/Explanation
Ans: a statement involving the application of the Horizontal Line Test or equivalent A1
[1 mark]
▶️Answer/Explanation
Ans: \(y = k\sqrt x \)
for either \(x = k\sqrt y \) or \(x = \frac{{{y^2}}}{{{k^2}}}\) A1
\({f^{ – 1}}(x) = \frac{{{x^2}}}{{{k^2}}}\) A1
\({\text{dom}}\left( {{f^{ – 1}}(x)} \right) = \left[ {0,\infty } \right[\) A1
[3 marks]
▶️Answer/Explanation
Ans: \(\frac{{{x^2}}}{{{k^2}}} = k\sqrt x \,\,\,\,\,\)or equivalent method M1
\(k = \sqrt x \)
\(k = 2\) A1
[2 marks]
(i) Find the area enclosed by the two graphs.
(ii) The line x = c cuts the graphs of \(y = f(x)\) and \(y = {f^{ – 1}}(x)\) at the points P and Q respectively. Given that the tangent to \(y = f(x)\) at point P is parallel to the tangent to \(y = {f^{ – 1}}(x)\) at point Q find the value of c .
▶️Answer/Explanation
Ans: (i) \(A = \int_a^b {({y_1} – {y_2}){\text{d}}x} \) (M1)
\(A = \int_0^4 {\left( {2{x^{\frac{1}{2}}} – \frac{1}{4}{x^2}} \right){\text{d}}x} \) A1
\( = \left[ {\frac{4}{3}{x^{\frac{3}{2}}} – \frac{1}{{12}}{x^3}} \right]_0^4\) A1
\( = \frac{{16}}{3}\) A1
(ii) attempt to find either \(f'(x)\) or \(({f^{ – 1}})'(x)\) M1
\(f'(x) = \frac{1}{{\sqrt x }},{\text{ }}\left( {({f^{ – 1}})'(x) = \frac{x}{2}} \right)\) A1A1
\(\frac{1}{{\sqrt c }} = \frac{c}{2}\) M1
\(c = {2^{\frac{2}{3}}}\) A1
[9 marks]
Total [16 marks]
Question
The graph of \(y = \frac{{a + x}}{{b + cx}}\) is drawn below.
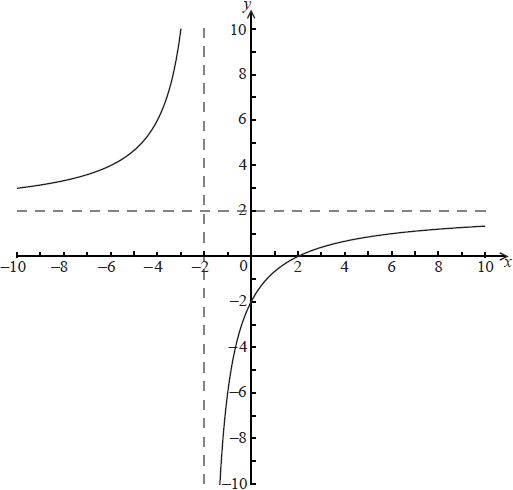
(a) Find the value of a, the value of b and the value of c.
▶️Answer/Explanation
Ans: an attempt to use either asymptotes or intercepts (M1)
\(a = – 2,{\text{ }}b = 1,{\text{ }}c = \frac{1}{2}\) A1A1A1
▶️Answer/Explanation
Ans: 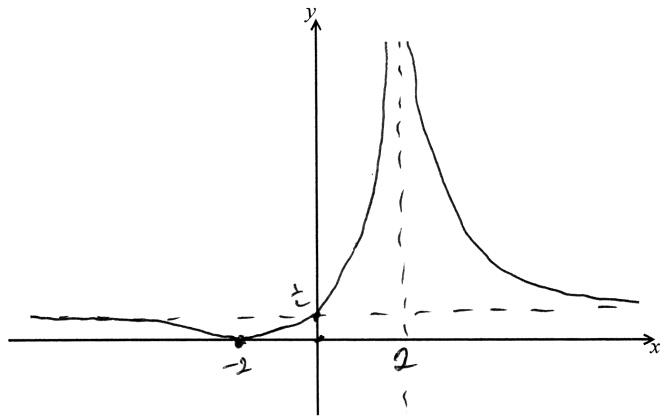
A4
Note: Award A1 for both asymptotes,
A1 for both intercepts,
A1, A1 for the shape of each branch, ignoring shape at \((x = – 2)\).
[8 marks]
Question
The diagram below shows the graph of the function \(y = f(x)\) , defined for all \(x \in \mathbb{R}\), where \(b > a > 0\) .
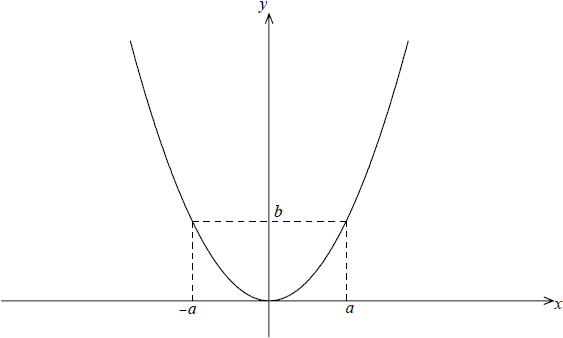
Consider the function \(g(x) = \frac{1}{{f(x – a) – b}}\).
a. Find the largest possible domain of the function \(g\) .[2]
▶️Answer/Explanation
Ans: \(f(x – a) \ne b\) (M1)
\(x \ne 0\) and \(x \ne 2a\) (or equivalent) A1
[2 marks]
 [6]
[6]
▶️Answer/Explanation
Ans: vertical asymptotes \(x = 0\), \(x = 2a\) A1
horizontal asymptote \(y = 0\) A1
Note: Equations must be seen to award these marks.
maximum \(\left( {a, – \frac{1}{b}} \right)\) A1A1
Note: Award A1 for correct x-coordinate and A1 for correct y-coordinate.
one branch correct shape A1
other 2 branches correct shape A1
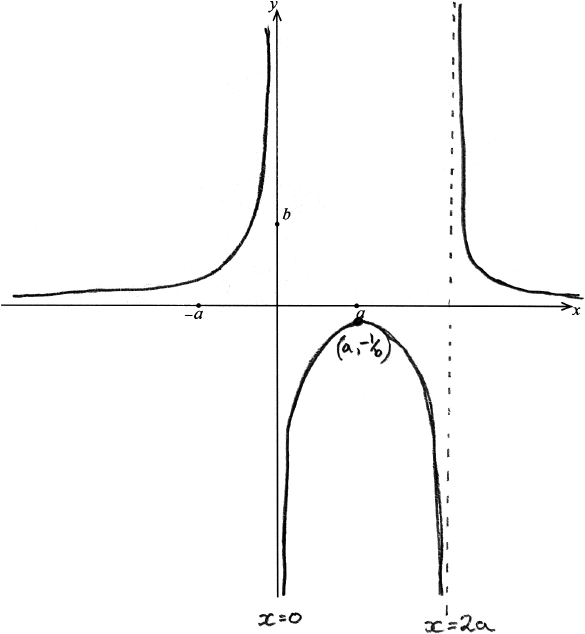
[6 marks]
Question
The graphs of \(y = \left| {x + 1} \right|\) and \(y = \left| {x – 3} \right|\) are shown below.
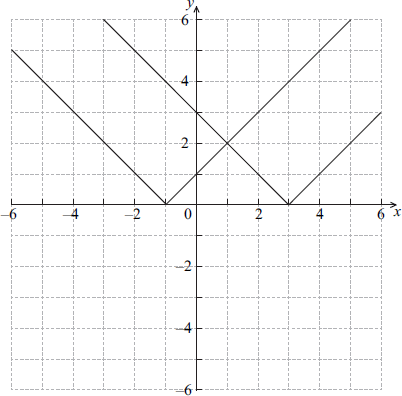
Let f (x) = \(\left| {\,x + 1\,} \right| – \left| {\,x – 3\,} \right|\).
a. Draw the graph of y = f (x) on the blank grid below. [4]
[4]
▶️Answer/Explanation
Ans: 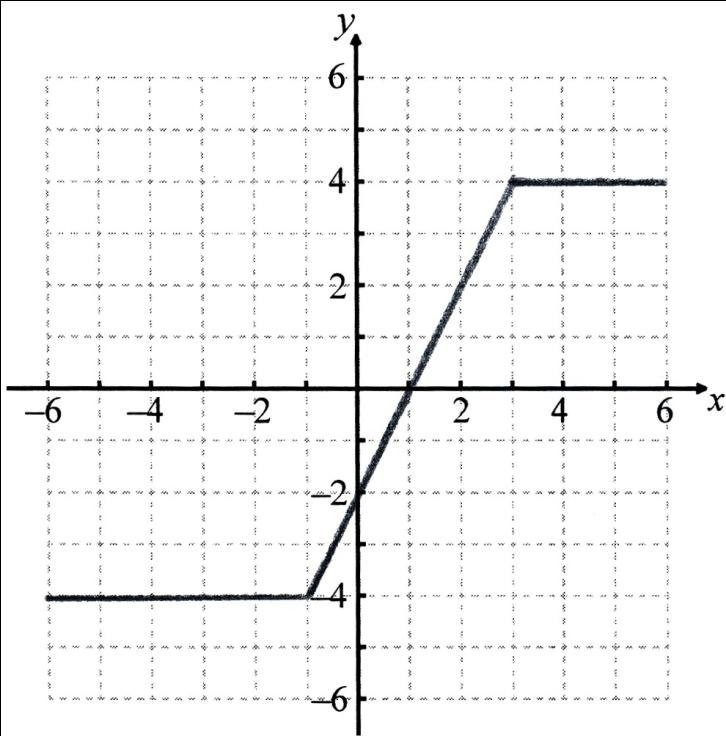
M1A1A1A1
Note: Award M1 for any of the three sections completely correct, A1 for each correct segment of the graph.
[4 marks]
(i) \(f'( – 3)\);
(ii) \(f'(2.7)\);
(iii) \(\int_{ – 3}^{ – 2} {f(x)dx} \).[4]
▶️Answer/Explanation
Ans:
(i) 0 A1
(ii) 2 A1
(iii) finding area of rectangle (M1)
\( – 4\) A1
Note: Award M1A0 for the answer 4.
[4 marks]
