Download IITian Academy App for accessing Online Mock Tests and More..
Question
The graph of \(y = (x – 1)\sin x\) , for \(0 \le x \le \frac{{5\pi }}{2}\) , is shown below.
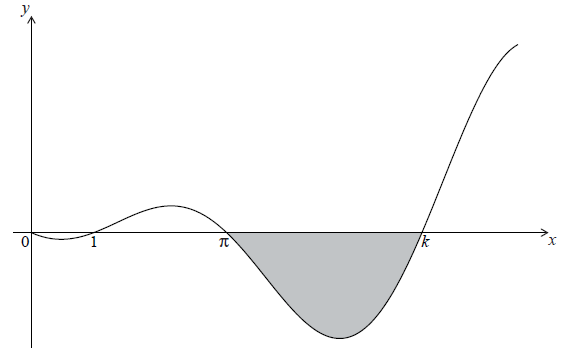
The graph has \(x\)-intercepts at \(0\), \(1\), \( \pi\) and \(k\) .
Find k .
The shaded region is rotated \(360^\circ \) about the x-axis. Let V be the volume of the solid formed.
Write down an expression for V .
The shaded region is rotated \(360^\circ \) about the x-axis. Let V be the volume of the solid formed.
Find V .
Answer/Explanation
Markscheme
evidence of valid approach (M1)
e.g. \(y = 0\) , \(\sin x = 0\)
\(2\pi = 6.283185 \ldots \)
\(k = 6.28\) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula (M1)
(accept absence of \({\rm{d}}x\) )
e.g. \(V = \pi \int_\pi ^k {{{(f(x))}^2}{\rm{d}}x} \) , \(\pi \int {{{((x – 1)\sin x)}^2}} \) , \(\pi \int_\pi ^{6.28 \ldots } {{y^2}{\rm{d}}x} \)
correct expression A2 N3
e.g. \(\pi \int_\pi ^{6.28} {{{(x – 1)}^2}{{\sin }^2}x{\rm{d}}x} \) , \(\pi \int_\pi ^{2\pi } {{{((x – 1)\sin x)}^2}{\rm{d}}x} \)
[3 marks]
\(V = 69.60192562 \ldots \)
\(V = 69.6\) A2 N2
[2 marks]
Question
The following diagram shows two ships A and B. At noon, ship A was 15 km due north of ship B. Ship A was moving south at 15 km h–1 and ship B was moving east at 11 km h–1.
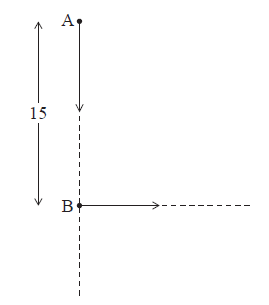
Find the distance between the ships
(i) at 13:00;
(ii) at 14:00.
Let \(s(t)\) be the distance between the ships t hours after noon, for \(0 \le t \le 4\) .
Show that \(s(t) = \sqrt {346{t^2} – 450t + 225} \) .
Sketch the graph of \(s(t)\) .
Due to poor weather, the captain of ship A can only see another ship if they are less than 8 km apart. Explain why the captain cannot see ship B between noon and 16:00.
Answer/Explanation
Markscheme
(i) evidence of valid approach (M1)
e.g. ship A where B was, B \(11{\text{ km}}\) away
\({\text{distance}} = 11\) A1 N2
(ii) evidence of valid approach (M1)
e.g. new diagram, Pythagoras, vectors
\(s = \sqrt {{{15}^2} + {{22}^2}} \) (A1)
\(\sqrt {709} = 26.62705\)
\(s = 26.6\) A1 N2
Note: Award M0A0A0 for using the formula given in part (b).
[5 marks]
evidence of valid approach (M1)
e.g. a table, diagram, formula \(d = r \times t\)
distance ship A travels t hours after noon is \(15(t – 1)\) (A2)
distance ship B travels in t hours after noon is \(11t\) (A1)
evidence of valid approach M1
e.g. \(s(t) = \sqrt {{{\left[ {15(t – 1)} \right]}^2} + {{(11t)}^2}} \)
correct simplification A1
e.g. \(\sqrt {225({t^2} – 2t + 1) + 121{t^2}} \)
\(s(t) = \sqrt {346{t^2} – 450t + 225} \) AG N0
[6 marks]
A1A1A1 N3
Note: Award A1 for shape, A1 for minimum at approximately \((0.7{\text{, }}9)\), A1 for domain.
[3 marks]
evidence of valid approach (M1)
e.g. \(s'(t) = 0\) , find minimum of \(s(t)\) , graph, reference to “more than 8 km”
\(\min = 8.870455 \ldots \) (accept 2 or more sf) A1
since \({s_{\min}} > 8\) , captain cannot see ship B R1 N0
[3 marks]
Question
Let \(f(x) = \cos ({{\rm{e}}^x})\) , for \( – 2 \le x \le 2\) .
Find \(f'(x)\) .
On the grid below, sketch the graph of \(f'(x)\) .
Answer/Explanation
Markscheme
\(f'(x) = – {{\rm{e}}^x}\sin ({{\rm{e}}^x})\) A1A1 N2
[2 marks]
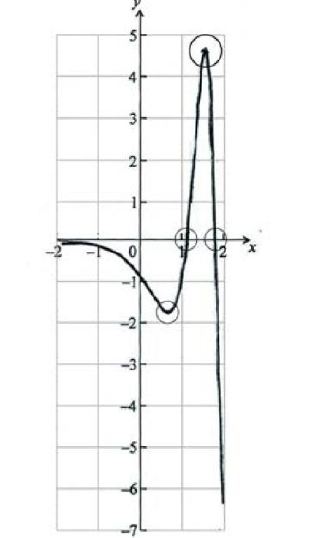A1A1A1A1 N4
Note: Award A1 for shape that must have the correct domain (from \( – 2\) to \( + 2\) ) and correct range (from \( – 6\) to \(4\) ), A1 for minimum in circle, A1 for maximum in circle and A1 for intercepts in circles.
[4 marks]
Question
Consider the following circle with centre O and radius r .
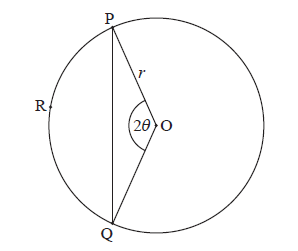
The points P, R and Q are on the circumference, \({\rm{P}}\widehat {\rm{O}}{\rm{Q}} = 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
Use the cosine rule to show that \({\rm{PQ}} = 2r\sin \theta \) .
Let l be the length of the arc PRQ .
Given that \(1.3{\rm{PQ}} – l = 0\) , find the value of \(\theta \) .
Consider the function \(f(\theta ) = 2.6\sin \theta – 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
(i) Sketch the graph of f .
(ii) Write down the root of \(f(\theta ) = 0\) .
Use the graph of f to find the values of \(\theta \) for which \(l < 1.3{\rm{PQ}}\) .
Answer/Explanation
Markscheme
correct substitution into cosine rule A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = {r^2} + {r^2} – 2(r)(r)\cos (2\theta )\) , \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2}(\cos (2\theta ))\)
substituting \(1 – 2{\sin ^2}\theta \) for \(\cos 2\theta \) (seen anywhere) A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2}(1 – 2{\sin ^2}\theta )\)
working towards answer (A1)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2} + 4{r^2}{\sin ^2}\theta \)
recognizing \(2{r^2} – 2{r^2} = 0\) (including crossing out) (seen anywhere)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 4{r^2}{\sin ^2}\theta \) , \({\rm{PQ}} = \sqrt {4{r^2}{{\sin }^2}\theta } \)
\({\rm{PQ = 2}}r{\rm{sin}}\theta \) AG N0
[4 marks]
\({\rm{PRQ}} = r \times 2\theta \) (seen anywhere) (A1)
correct set up A1
e.g. \(1.3 \times 2r\sin \theta – r \times (2\theta ) = 0\)
attempt to eliminate r (M1)
correct equation in terms of the one variable \(\theta \) (A1)
e.g. \(1.3 \times 2\sin \theta – 2\theta = 0\)
1.221496215
\(\theta = 1.22\) (accept \(70.0^\circ \) (69.9)) A1 N3
[5 marks]
(i)
A1A1A1 N3
Note: Award A1 for approximately correct shape, A1 for x-intercept in approximately correct position, A1 for domain. Do not penalise if sketch starts at origin.
(ii) \(1.221496215\)
\(\theta = 1.22\) A1 N1
[4 marks]
evidence of appropriate approach (may be seen earlier) M2
e.g. \(2\theta < 2.6\sin \theta \) , \(0 < f(\theta )\) , showing positive part of sketch
\(0 < \theta < 1.221496215\)
\(0 < \theta = 1.22\) (accept \(\theta < 1.22\) ) A1 N1
[3 marks]
Question
A particle’s displacement, in metres, is given by \(s(t) = 2t\cos t\) , for \(0 \le t \le 6\) , where t is the time in seconds.
On the grid below, sketch the graph of \(s\) .
Find the maximum velocity of the particle.
Answer/Explanation
Markscheme
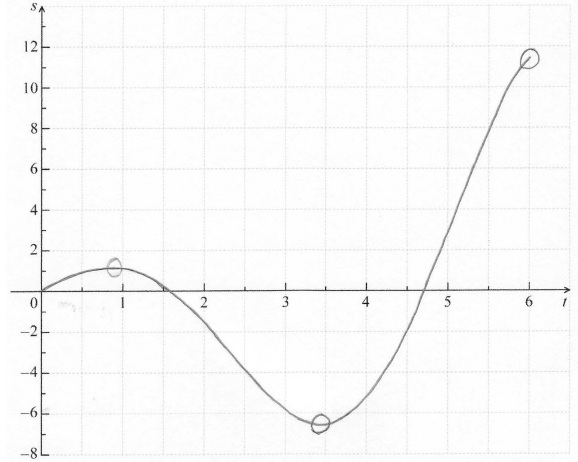A1A1A1A1 N4
Note: Award A1 for approximately correct shape (do not accept line segments).
Only if this A1 is awarded, award the following:
A1 for maximum and minimum within circles,
A1 for x-intercepts between 1 and 2 and between 4 and 5,
A1 for left endpoint at \((0{\text{, }}0)\) and right endpoint within circle.
[4 marks]
appropriate approach (M1)
e.g. recognizing that \(v = s’\) , finding derivative, \(a = s”\)
valid method to find maximum (M1)
e.g. sketch of \(v\) , \(v'(t) = 0\) , \(t = 5.08698 \ldots \)
\(v = 10.20025 \ldots \)
\(v = 10.2\) \([10.2{\text{, }}10.3]\) A1 N2
[3 marks]
Question
Consider the function \(f(x) = {x^2} – 4x + 1\) .
Sketch the graph of f , for \( – 1 \le x \le 5\) .
This function can also be written as \(f(x) = {(x – p)^2} – 3\) .
Write down the value of p .
The graph of g is obtained by reflecting the graph of f in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0\\
6
\end{array}} \right)\) .
Show that \(g(x) = – {x^2} + 4x + 5\) .
The graph of g is obtained by reflecting the graph of f in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0\\
6
\end{array}} \right)\) .
The graphs of f and g intersect at two points.
Write down the x-coordinates of these two points.
The graph of \(g\) is obtained by reflecting the graph of \(f\) in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0 \\
6
\end{array}} \right)\) .
Let R be the region enclosed by the graphs of f and g .
Find the area of R .
Answer/Explanation
Markscheme
A1A1A1A1 N4
Note: The shape must be an approximately correct upwards parabola.
Only if the shape is approximately correct, award the following:
A1 for vertex \(x \approx 2\) , A1 for x-intercepts between 0 and 1, and 3 and 4, A1 for correct y-intercept \((0{\text{, }}1)\), A1 for correct domain \([ – 1{\text{, }}5]\).
Scale not required on the axes, but approximate positions need to be clear.
[4 marks]
\(p = 2\) A1 N1
[1 mark]
correct vertical reflection, correct vertical translation (A1)(A1)
e.g. \( – f(x)\) , \( – ({(x – 2)^2} – 3)\) , \( – y\) , \( – f(x) + 6\) , \(y + 6\)
transformations in correct order (A1)
e.g. \( – ({x^2} – 4x + 1) + 6\) , \( – ({(x – 2)^2} – 3) + 6\)
simplification which clearly leads to given answer A1
e.g. \( – {x^2} + 4x – 1 + 6\) , \( – ({x^2} – 4x + 4 – 3) + 6\)
\(g(x) = – {x^2} + 4x + 5\) AG N0
Note: If working shown, award A1A1A0A0 if transformations correct, but done in reverse order, e.g. \( – ({x^2} – 4x + 1 + 6)\).
[4 marks]
valid approach (M1)
e.g. sketch, \(f = g\)
\( – 0.449489 \ldots \) , \(4.449489 \ldots \)
\((2 \pm \sqrt 6 )\) (exact), \( – 0.449{\text{ }}[ – 0.450{\text{, }} – 0.449]\) ; \(4.45{\text{ }}[4.44{\text{, }}4.45]\) A1A1 N3
[3 marks]
attempt to substitute limits or functions into area formula (accept absence of \({\rm{d}}x\) ) (M1)
e.g. \(\int_a^b {(( – {x^2}} + 4x + 5) – ({x^2} – 4x + 1)){\rm{d}}x\) , \(\int_{4.45}^{ – 0.449} {(f – g)} \) , \(\int {( – 2{x^2}} + 8x + 4){\rm{d}}x\)
approach involving subtraction of integrals/areas (accept absence of \({\rm{d}}x\) ) (M1)
e.g. \(\int_a^b {( – {x^2}} + 4x + 5) – \int_a^b {({x^2}} – 4x + 1)\) , \(\int {(f – g){\rm{d}}x} \)
\({\rm{area}} = 39.19183 \ldots \)
\({\rm{area}} = 39.2\) \([39.1{\text{, }}39.2]\) A1 N3
[3 marks]
Question
Let \(G(x) = 95{{\text{e}}^{( – 0.02x)}} + 40\), for \(20 \le x \le 200\).
On the following grid, sketch the graph of \(G\).
Robin and Pat are planning a wedding banquet. The cost per guest, \(G\) dollars, is modelled by the function \(G(n) = 95{{\text{e}}^{( – 0.02n)}} + 40\), for \(20 \le n \le 200\), where \(n\) is the number of guests.
Calculate the total cost for \(45\) guests.
Answer/Explanation
Markscheme
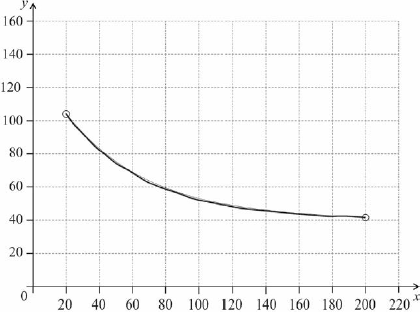A1A1A1 N3
Note: Curve must be approximately correct exponential shape (concave up and decreasing). Only if the shape is approximately correct, award the following:
A1 for left endpoint in circle,
A1 for right endpoint in circle,
A1 for asymptotic to \(y = 40\) (must not go below \(y = 40\)).
[3 marks]
attempt to find \(G(45)\) (M1)
eg\(\;\;\;78.6241\), value read from their graph
multiplying cost times number of people (M1)
eg\(\;\;\;45 \times 78.6241,{\text{ }}G(45) \times 45\)
\(3538.08\)
\(3540\) (dollars) A1 N2
[3 marks]
Total [6 marks]
Question
Let \(f(x) = {x^2} – 1\) and \(g(x) = {x^2} – 2\), for \(x \in \mathbb{R}\).
Show that \((f \circ g)(x) = {x^4} – 4{x^2} + 3\).
On the following grid, sketch the graph of \((f \circ g)(x)\), for \(0 \leqslant x \leqslant 2.25\).
The equation \((f \circ g)(x) = k\) has exactly two solutions, for \(0 \leqslant x \leqslant 2.25\). Find the possible values of \(k\).
Answer/Explanation
Markscheme
attempt to form composite in either order (M1)
eg\(\,\,\,\,\,\)\(f({x^2} – 2),{\text{ }}{({x^2} – 1)^2} – 2\)
\(({x^4} – 4{x^2} + 4) – 1\) A1
\((f \circ g)(x) = {x^4} – 4{x^2} + 3\) AG N0
[2 marks]
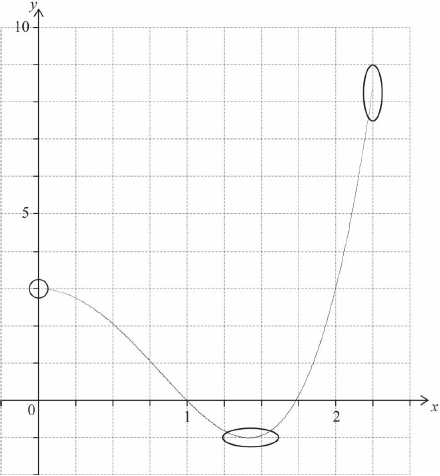A1
A1A1 N3
Note: Award A1 for approximately correct shape which changes from concave down to concave up. Only if this A1 is awarded, award the following:
A1 for left hand endpoint in circle and right hand endpoint in oval,
A1 for minimum in oval.
[3 marks]
evidence of identifying max/min as relevant points (M1)
eg\(\,\,\,\,\,\)\(x = 0,{\text{ }}1.41421,{\text{ }}y = – 1,{\text{ }}3\)
correct interval (inclusion/exclusion of endpoints must be correct) A2 N3
eg\(\,\,\,\,\,\)\( – 1 < k \leqslant 3,{\text{ }}\left] { – 1,{\text{ 3}}} \right],{\text{ }}( – 1,{\text{ }}3]\)
[3 marks]
Question
Let \(f(x) = \frac{{6{x^2} – 4}}{{{{\text{e}}^x}}}\), for \(0 \leqslant x \leqslant 7\).
Find the \(x\)-intercept of the graph of \(f\).
The graph of \(f\) has a maximum at the point A. Write down the coordinates of A.
On the following grid, sketch the graph of \(f\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }} \pm 0.816\)
0.816496
\(x = \sqrt {\frac{2}{3}} \) (exact), 0.816 A1 N2
[2 marks]
\((2.29099,{\text{ }}2.78124)\)
\({\text{A}}(2.29,{\text{ }}2.78)\) A1A1 N2
[2 marks]
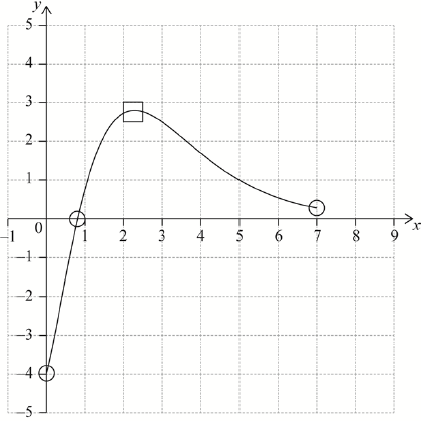A1A1A1 N3
Notes: Award A1 for correct domain and endpoints at \(x = 0\) and \(x = 7\) in circles,
A1 for maximum in square,
A1 for approximately correct shape that passes through their \(x\)-intercept in circle and has changed from concave down to concave up between 2.29 and 7.
[3 marks]
Question
Let g(x) = −(x − 1)2 + 5.
Let f(x) = x2. The following diagram shows part of the graph of f.
The graph of g intersects the graph of f at x = −1 and x = 2.
Write down the coordinates of the vertex of the graph of g.
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
Find the area of the region enclosed by the graphs of f and g.
Answer/Explanation
Markscheme
(1,5) (exact) A1 N1
[1 mark]
A1A1A1 N3
Note: The shape must be a concave-down parabola.
Only if the shape is correct, award the following for points in circles:
A1 for vertex,
A1 for correct intersection points,
A1 for correct endpoints.
[3 marks]
integrating and subtracting functions (in any order) (M1)
eg \(\int {f – g} \)
correct substitution of limits or functions (accept missing dx, but do not accept any errors, including extra bits) (A1)
eg \(\int_{ – 1}^2 {g – f,\,\,\int { – {{\left( {x – 1} \right)}^2}} } + 5 – {x^2}\)
area = 9 (exact) A1 N2
[3 marks]