Question
Consider the quartic equation z4 + 4z3 + 8z2 + 80z + 400 = 0 , z \(\in \mathbb{C}\).
Two of the roots of this equation are a + bi and b + ai , where a , b ∈ \(\mathbb{Z}\)
Find the possible values of a .
▶️Answer/Explanation
Ans:
METHOD 1
other two roots are a – bi and b – ai
sum of roots = −4 and product of roots = 400
attempt to set sum of four roots equal to −4 or 4 OR
attempt to set product of four roots equal to 400
a + bi+a −bi+ b + ai +b − ai = − 4
2a + 2b = -4 \((\Rightarrow a+ b = -2)\)
(a+bi)(a-bi)(b+ai)(b-ai)= 400
(a2+b2)2 = 400
a2+b2= 20
attempt to solve simultaneous equations other two roots are
a =2 or a= 4
METHOD 2
other two roots are a-bi and b-ai
(z −(a +bi))(z −(a −bi))(z −(b + ai))(z −(b − ai))(= 0) A1
((z − a)2 + b2 )((z −b)2 + a2 )(= 0)
(z2 − 2az + a2 + b2 )(z2 − 2bz + b2 + a2 )(= 0) A1
Attempt to equate coefficient of z3 and constant with the given quartic equation M1
-2a=2b=4 and (a2+b2)2 = 400
attempt to solve simultaneous equations (M1)
a = 2 or a = −4 A1A1
Question
The same remainder is found when \(2{x^3} + k{x^2} + 6x + 32\) and \({x^4} – 6{x^2} – {k^2}x + 9\) are divided by \(x + 1\) . Find the possible values of k .
▶️Answer/Explanation
Markscheme
let \(f(x) = 2{x^3} + k{x^2} + 6x + 32\)
let \(g(x) = {x^4} – 6{x^2} – {k^2}x + 9\)
\(f( – 1) = – 2 + k – 6 + 32( = 24 + k)\) A1
\(g( – 1) = 1 – 6 + {k^2} + 9( = 4 + {k^2})\) A1
\( \Rightarrow 24 + k = 4 + {k^2}\) M1
\( \Rightarrow {k^2} – k – 20 = 0\)
\( \Rightarrow (k – 5)(k + 4) = 0\) (M1)
\( \Rightarrow k = 5,\, – 4\) A1A1
[6 marks]
Question
The function f is defined by \(f(x) = \frac{1}{{4{x^2} – 4x + 5}}\).
Express \(4{x^2} – 4x + 5\) in the form \(a{(x – h)^2} + k\) where a, h, \(k \in \mathbb{Q}\).[2]
The graph of \(y = {x^2}\) is transformed onto the graph of \(y = 4{x^2} – 4x + 5\). Describe a sequence of transformations that does this, making the order of transformations clear.[3]
Sketch the graph of \(y = f(x)\).[2]
Find the range of f.[2]
By using a suitable substitution show that \(\int {f(x){\text{d}}x = \frac{1}{4}\int {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \).[3]
Prove that \(\int_1^{3.5} {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \frac{\pi }{{16}}} \).[7]
▶️Answer/Explanation
Markscheme
\(4{(x – 0.5)^2} + 4\) A1A1
Note: A1 for two correct parameters, A2 for all three correct.
[2 marks]
translation \(\left( {\begin{array}{*{20}{c}}
{0.5} \\
0
\end{array}} \right)\) (allow “0.5 to the right”) A1
stretch parallel to y-axis, scale factor 4 (allow vertical stretch or similar) A1
translation \(\left( {\begin{array}{*{20}{c}}
0 \\
4
\end{array}} \right)\) (allow “4 up”) A1
Note: All transformations must state magnitude and direction.
Note: First two transformations can be in either order.
It could be a stretch followed by a single translation of \(\left( {\begin{array}{*{20}{c}}
{0.5} \\
4
\end{array}} \right)\). If the vertical translation is before the stretch it is \(\left( {\begin{array}{*{20}{c}}
0 \\
1
\end{array}} \right)\).
[3 marks]
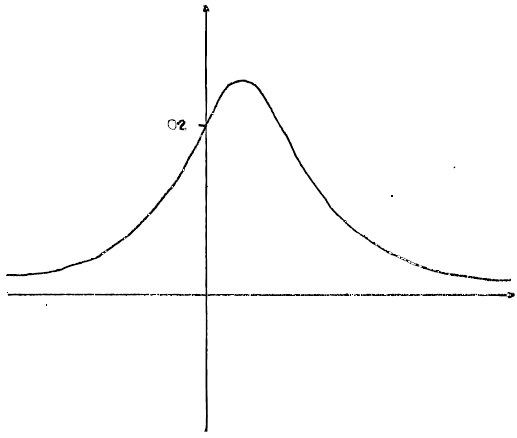
general shape (including asymptote and single maximum in first quadrant), A1
intercept \(\left( {0,\frac{1}{5}} \right)\) or maximum \(\left( {\frac{1}{2},\frac{1}{4}} \right)\) shown A1
[2 marks]
\(0 < f(x) \leqslant \frac{1}{4}\) A1A1
Note: A1 for \( \leqslant \frac{1}{4}\), A1 for \(0 < \).
[2 marks]
let \(u = x – \frac{1}{2}\) A1
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = 1\,\,\,\,\,{\text{(or d}}u = {\text{d}}x)\) A1
\(\int {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \int {\frac{1}{{4{{\left( {x – \frac{1}{2}} \right)}^2} + 4}}{\text{d}}x} } \) A1
\(\int {\frac{1}{{4{u^2} + 4}}{\text{d}}u = \frac{1}{4}\int {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \) AG
Note: If following through an incorrect answer to part (a), do not award final A1 mark.
[3 marks]
\(\int_1^{3.5} {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \frac{1}{4}\int_{0.5}^3 {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \) A1
Note: A1 for correct change of limits. Award also if they do not change limits but go back to x values when substituting the limit (even if there is an error in the integral).
\(\frac{1}{4}\left[ {\arctan (u)} \right]_{0.5}^3\) (M1)
\(\frac{1}{4}\left( {\arctan (3) – \arctan \left( {\frac{1}{2}} \right)} \right)\) A1
let the integral = I
\(\tan 4I = \tan \left( {\arctan (3) – \arctan \left( {\frac{1}{2}} \right)} \right)\) M1
\(\frac{{3 – 0.5}}{{1 + 3 \times 0.5}} = \frac{{2.5}}{{2.5}} = 1\) (M1)A1
\(4I = \frac{\pi }{4} \Rightarrow I = \frac{\pi }{{16}}\) A1AG
[7 marks]
Question
Consider the polynomial \(q(x) = 3{x^3} – 11{x^2} + kx + 8\).
Given that \(q(x)\) has a factor \((x – 4)\), find the value of \(k\).[3]
Hence or otherwise, factorize \(q(x)\) as a product of linear factors.[3]
▶️Answer/Explanation
Markscheme
\(q(4) = 0\) (M1)
\(192 – 176 + 4k + 8 = 0{\text{ }}(24 + 4k = 0)\) A1
\(k = – 6\) A1
[3 marks]
\(3{x^3} – 11{x^2} – 6x + 8 = (x – 4)(3{x^2} + px – 2)\)
equate coefficients of \({x^2}\): (M1)
\( – 12 + p = – 11\)
\(p = 1\)
\((x – 4)(3{x^2} + x – 2)\) (A1)
\((x – 4)(3x – 2)(x + 1)\) A1
Note: Allow part (b) marks if any of this work is seen in part (a).
Note: Allow equivalent methods (eg, synthetic division) for the M marks in each part.
[3 marks]
Question
Consider the polynomial \(f(x) =4x^3-4x^2-5x+3.\)
(a) Show that x = –1 is a root and find the other two roots by using long division.
(b) Express the polynomial in the form f(x) = (x – a)(bx – c)(dx – e), where a,b,c,d,e∈Z.
▶️Answer/Explanation
Ans
(a) \(x = -1, x=\frac{1}{2}, x = \frac{3}{2}\) (b) f(x) = (x+1)(2x-1)(2x-3)
