Download IITian Academy App for accessing Online Mock Tests and More..
Question
A city is concerned about pollution, and decides to look at the number of people using taxis. At the end of the year 2000, there were 280 taxis in the city. After n years the number of taxis, T, in the city is given by\[T = 280 \times {1.12^n} .\]
(i) Find the number of taxis in the city at the end of 2005.
(ii) Find the year in which the number of taxis is double the number of taxis there were at the end of 2000.
At the end of 2000 there were \(25600\) people in the city who used taxis.
After n years the number of people, P, in the city who used taxis is given by\[P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1n}}}} .\](i) Find the value of P at the end of 2005, giving your answer to the nearest whole number.
(ii) After seven complete years, will the value of P be double its value at the end of 2000? Justify your answer.
Let R be the ratio of the number of people using taxis in the city to the number of taxis. The city will reduce the number of taxis if \(R < 70\) .
(i) Find the value of R at the end of 2000.
(ii) After how many complete years will the city first reduce the number of taxis?
Answer/Explanation
Markscheme
(i) \(n = 5\) (A1)
\(T = 280 \times {1.12^5}\)
\(T = 493\) A1 N2
(ii) evidence of doubling (A1)
e.g. 560
setting up equation A1
e.g. \(280 \times {1.12^n} = 560\), \({1.12^n} = 2\)
\(n = 6.116 \ldots \) (A1)
in the year 2007 A1 N3
[6 marks]
(i) \(P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1(5)}}}}\) (A1)
\(P = 39635.993 \ldots \) (A1)
\(P = 39636\) A1 N3
(ii) \(P = \frac{{2560000}}{{10 + 90{{\rm{e}}^{ – 0.1(7)}}}}\)
\(P = 46806.997 \ldots \) A1
not doubled A1 N0
valid reason for their answer R1
e.g. \(P < 51200\)
[6 marks]
(i) correct value A2 N2
e.g. \(\frac{{25600}}{{280}}\) , 91.4, \(640:7\)
(ii) setting up an inequality (accept an equation, or reversed inequality) M1
e.g. \(\frac{P}{T} < 70\) , \(\frac{{2560000}}{{(10 + 90{{\rm{e}}^{ – 0.1n}})280 \times {{1.12}^n}}} < 70\)
finding the value \(9.31 \ldots \) (A1)
after 10 years A1 N2
[5 marks]
Question
Let \(f(x) = A{{\rm{e}}^{kx}} + 3\) . Part of the graph of f is shown below.
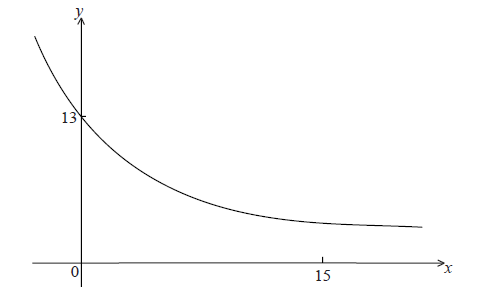
The y-intercept is at (0, 13) .
Show that \(A = 10\) .
Given that \(f(15) = 3.49\) (correct to 3 significant figures), find the value of k.
(i) Using your value of k , find \(f'(x)\) .
(ii) Hence, explain why f is a decreasing function.
(iii) Write down the equation of the horizontal asymptote of the graph f .
Let \(g(x) = – {x^2} + 12x – 24\) .
Find the area enclosed by the graphs of f and g .
Answer/Explanation
Markscheme
substituting (0, 13) into function M1
e.g. \(13 = A{{\rm{e}}^0} + 3\)
\(13 = A + 3\) A1
\(A = 10\) AG N0
[2 marks]
substituting into \(f(15) = 3.49\) A1
e.g. \(3.49 = 10{{\rm{e}}^{15k}} + 3\) , \(0.049 = {{\rm{e}}^{15k}}\)
evidence of solving equation (M1)
e.g. sketch, using \(\ln \)
\(k = – 0.201\) (accept \(\frac{{\ln 0.049}}{{15}}\) ) A1 N2
[3 marks]
(i) \(f(x) = 10{{\rm{e}}^{ – 0.201x}} + 3\)
\(f(x) = 10{{\rm{e}}^{ – 0.201x}} \times – 0.201\) \(( = – 2.01{{\rm{e}}^{ – 0.201x}})\) A1A1A1 N3
Note: Award A1 for \(10{{\rm{e}}^{ – 0.201x}}\) , A1 for \( \times – 0.201\) , A1 for the derivative of 3 is zero.
(ii) valid reason with reference to derivative R1 N1
e.g. \(f'(x) < 0\) , derivative always negative
(iii) \(y = 3\) A1 N1
[5 marks]
finding limits \(3.8953 \ldots \), \(8.6940 \ldots \) (seen anywhere) A1A1
evidence of integrating and subtracting functions (M1)
correct expression A1
e.g. \(\int_{3.90}^{8.69} {g(x) – f(x){\rm{d}}x} \) , \(\int_{3.90}^{8.69} {\left[ {\left( { – {x^2} + 12x – 24} \right) – \left( {10{{\rm{e}}^{ – 0.201x}} + 3} \right)} \right]} {\rm{d}}x\)
area \(= 19.5\) A2 N4
[6 marks]
Question
The number of bacteria, n , in a dish, after t minutes is given by \(n = 800{{\rm{e}}^{0.13t}}\) .
Find the value of n when \(t = 0\) .
Find the rate at which n is increasing when \(t = 15\) .
Answer/Explanation
Markscheme
\(n = 800{{\rm{e}}^0}\) (A1)
\(n = 800\) A1 N2
[2 marks]
evidence of using the derivative (M1)
\(n'(15) = 731\) A1 N2
[2 marks]
METHOD 1
setting up inequality (accept equation or reverse inequality) A1
e.g. \(n'(t) > 10000\)
evidence of appropriate approach M1
e.g. sketch, finding derivative
\(k = 35.1226 \ldots \) (A1)
least value of k is 36 A1 N2
METHOD 2
\(n'(35) = 9842\) , and \(n'(36) = 11208\) A2
least value of k is 36 A2 N2
[4 marks]
Question
Jose takes medication. After t minutes, the concentration of medication left in his bloodstream is given by \(A(t) = 10{(0.5)^{0.014t}}\) , where A is in milligrams per litre.
Write down \(A(0)\) .
Find the concentration of medication left in his bloodstream after 50 minutes.
At 13:00, when there is no medication in Jose’s bloodstream, he takes his first dose of medication. He can take his medication again when the concentration of medication reaches 0.395 milligrams per litre. What time will Jose be able to take his medication again?
Answer/Explanation
Markscheme
\(A(0) = 10\) A1 N1
[1 mark]
substitution into formula (A1)
e.g. \(10{(0.5)^{0.014(50)}}\) , \(A(50)\)
\(A(50) = 6.16\) A1 N2
[2 marks]
set up equation (M1)
e.g. \(A(t) = 0.395\)
attempting to solve (M1)
e.g. graph, use of logs
correct working (A1)
e.g. sketch of intersection, \(0.014t\log 0.5 = \log 0.0395\)
\(t = 333.00025 \ldots \) A1
correct time 18:33 or 18:34 (accept 6:33 or 6:34 but nothing else) A1 N3
[5 marks]
Question
Let \(f(x) = {{\rm{e}}^{\frac{x}{4}}}\) and \(g(x) = mx\) , where \(m \ge 0\) , and \( – 5 \le x \le 5\) . Let \(R\) be the region enclosed by the \(y\)-axis, the graph of \(f\) , and the graph of \(g\) .
Let \(m = 1\).
(i) Sketch the graphs of \(f\) and \(g\) on the same axes.
(ii) Find the area of \(R\) .
Find the area of \(R\) .
Consider all values of \(m\) such that the graphs of \(f\) and \(g\) intersect. Find the value of \(m\) that gives the greatest value for the area of \(R\) .
Answer/Explanation
Markscheme
(i)
A1A1 N2
Notes: Award A1 for the graph of \(f\) positive, increasing and concave up.
Award A1 for graph of \(g\) increasing and linear with \(y\)-intercept of \(0\).
Penalize one mark if domain is not [\( – 5\), \(5\)] and/or if \(f\) and \(g\) do not intersect in the first quadrant.
[2 marks]
(ii)
attempt to find intersection of the graphs of \(f\) and \(g\) (M1)
eg \({{\rm{e}}^{\frac{x}{4}}} = x\)
\(x = 1.42961 \ldots \) A1
valid attempt to find area of \(R\) (M1)
eg \(\int {(x – {{\rm{e}}^{\frac{x}{4}}}} ){\rm{d}}x\) , \(\int_0^1 {(g – f)} \) , \(\int {(f – g)} \)
area \( = 0.697\) A2 N3
[5 marks]
attempt to find intersection of the graphs of \(f\) and \(g\) (M1)
eg \({{\rm{e}}^{\frac{x}{4}}} = x\)
\(x = 1.42961 \ldots \) A1
valid attempt to find area of \(R\) (M1)
eg \(\int {(x – {{\rm{e}}^{\frac{x}{4}}}} ){\rm{d}}x\) , \(\int_0^1 {(g – f)} \) , \(\int {(f – g)} \)
area \( = 0.697\) A2 N3
[5 marks]
recognize that area of \(R\) is a maximum at point of tangency (R1)
eg \(m = f'(x)\)
equating functions (M1)
eg \(f(x) = g(x)\) , \({{\rm{e}}^{\frac{x}{4}}} = mx\)
\(f'(x) = \frac{1}{4}{{\rm{e}}^{\frac{x}{4}}}\) (A1)
equating gradients (A1)
eg \(f'(x) = g'(x)\) , \(\frac{1}{4}{{\rm{e}}^{\frac{x}{4}}} = m\)
attempt to solve system of two equations for \(x\) (M1)
eg \(\frac{1}{4}{{\rm{e}}^{\frac{x}{4}}} \times x = {{\rm{e}}^{\frac{x}{4}}}\)
\(x = 4\) (A1)
attempt to find \(m\) (M1)
eg \(f'(4)\) , \(\frac{1}{4}{{\rm{e}}^{\frac{4}{4}}}\)
\(m = \frac{1}{4}e\) (exact), \(0.680\) A1 N3
[8 marks]
Question
The number of bacteria in two colonies, \(\rm{A}\) and \(\rm{B}\), starts increasing at the same time.
The number of bacteria in colony \(\rm{A}\) after \(t\) hours is modelled by the function \(\rm{A}(t) = 12{{\text{e}}^{0.4t}}\).
Find the number of bacteria in colony \({\text{A}}\) after four hours.
Find the number of bacteria in colony \({\text{A}}\) after four hours.
How long does it take for the number of bacteria in colony \({\text{A}}\) to reach \(400\)?
The number of bacteria in colony \({\text{B}}\) after \(t\) hours is modelled by the function \(B(t) = 24{{\text{e}}^{kt}}\).
After four hours, there are \(60\) bacteria in colony \({\text{B}}\). Find the value of \(k\).
The number of bacteria in colony \({\text{B}}\) after \(t\) hours is modelled by the function \(B(t) = 24{{\text{e}}^{kt}}\).
The number of bacteria in colony \({\text{A}}\) first exceeds the number of bacteria in colony \({\text{B}}\) after \(n\) hours, where \(n \in \mathbb{Z}\). Find the value of \(n\).
Answer/Explanation
Markscheme
correct substitution into formula (A1)
eg \(12{{\text{e}}^{0.4(0)}}\)
\(12\) bacteria in the dish A1 N2
[2 marks]
correct substitution into formula (A1)
eg \(12{{\text{e}}^{0.4(4)}}\)
\(59.4363\) (A1)
\(59\) bacteria in the dish (integer answer only) A1 N3
[3 marks]
correct equation (A1)
eg \(A(t) = 400,{\text{ }}12{{\text{e}}^{0.4t}} = 400\)
valid attempt to solve (M1)
eg graph, use of logs
\(8.76639\)
\(8.77\) (hours) A1 N3
[3 marks]
valid attempt to solve (M1)
eg \(n(4) = 60,{\text{ }}60 = 24{{\text{e}}^{4k}}\), use of logs
correct working (A1)
eg sketch of intersection, \(4k = \ln 2.5\)
\(k = 0.229072\)
\(k = \frac{{\ln 2.5}}{4}\) (exact), \(k = 0.229\) A1 N3
[3 marks]
METHOD 1
setting up an equation or inequality (accept any variable for \(n\)) (M1)
eg \(A(t) > B(t),{\text{ }}12{{\text{e}}^{0.4n}} = 24{{\text{e}}^{0.229n}},{\text{ }}{{\text{e}}^{0.4n}} = 2{{\text{e}}^{0.229n}}\)
correct working (A1)
eg sketch of intersection, \({{\text{e}}^{0.171n}} = 2\)
\(4.05521\) (accept \(4.05349\)) (A1)
\(n = 5\) (integer answer only) A1 N3
METHOD 2
\(A(4) = 59,{\text{ }}B(4) = 60\) (from earlier work)
\(A(5) = 88.668,{\text{ }}B(5) = 75.446\) A1A1
valid reasoning (R1)
eg \(A(4) < B(4)\) and \(A(5) > B(5)\)
\(n = 5\) (integer answer only) A1 N3
[4 marks]
Question
The price of a used car depends partly on the distance it has travelled. The following table shows the distance and the price for seven cars on 1 January 2010.
The relationship between \(x\) and \(y\) can be modelled by the regression equation \(y = ax + b\).
On 1 January 2010, Lina buys a car which has travelled \(11\,000{\text{ km}}\).
The price of a car decreases by 5% each year.
Lina will sell her car when its price reaches \(10\,000\) dollars.
(i) Find the correlation coefficient.
(ii) Write down the value of \(a\) and of \(b\).
Use the regression equation to estimate the price of Lina’s car, giving your answer to the nearest 100 dollars.
Calculate the price of Lina’s car after 6 years.
Find the year when Lina sells her car.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
(i) valid approach (M1)
eg\(\,\,\,\,\,\)correct value for \(r\) (or for \(a\) or \(b\) seen in (ii))
\( – 0.994347\)
\(r = – 0.994\) A1 N2
(ii) \( – 1.58095,{\text{ }}33480.3\)
\(a = – 1.58,{\text{ }}b = 33500\) A1A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
correct substitution into their regression equation
eg\(\,\,\,\,\,\)\( – 1.58095(11000){\text{ }} + 33480.3\) (A1)
\(16\,089.85{\text{ }}(16\,120{\text{ from 3sf}})\) (A1)
\({\text{price}} = 16\,100{\text{ }}({\text{dollars}})\) (must be rounded to the nearest 100 dollars) A1 N3
[3 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(P \times {({\text{rate}})^t}\)
\({\text{rate}} = 0.95\) (may be seen in their expression) (A1)
correct expression (A1)
eg\(\,\,\,\,\,\)\(16100 \times {0.95^6}\)
\(11\,834.97\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
METHOD 2
attempt to find all six terms (M1)
eg\(\,\,\,\,\,\)\(\left( {\left( {(16\,100 \times 0.95) \times 0.95} \right) \ldots } \right) \times 0.95\), table of values
5 correct values (accept values that round correctly to the nearest dollar)
\(15\,295,{\text{ }}14\,530,{\text{ }}13\,804,{\text{ }}13\,114,{\text{ }}12\,458\) A2
\(11\,835\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
correct equation (A1)
eg\(\,\,\,\,\,\)\(16\,100 \times {0.95^x}{\text{ = }}10\,000\)
valid attempt to solve (M1)
eg\(\,\,\,\,\,\)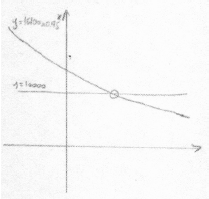
, using logs
9.28453 (A1)
year 2019 A1 N2
METHOD 2
valid approach using table of values (M1)
both crossover values (accept values that round correctly to the nearest dollar) A2
eg\(\,\,\,\,\,\)\({\text{P}} = 10\,147{\text{ }}({\text{1 Jan 2019}}),{\text{ P}} = 9\,639.7{\text{ }}({\text{1 Jan 2020}})\)
year 2019 A1 N2
[4 marks]
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
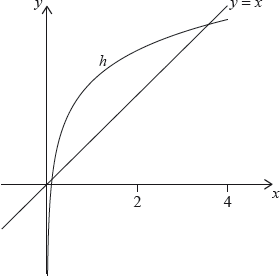
The graph of \(h\) intersects the graph of \({h^{ – 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) – x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ – 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Answer/Explanation
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)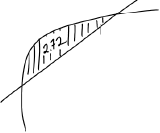
recognizing graphs of \(h\) and \({h^{ – 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ – 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x – {h^{ – 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) – x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) – x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]