Question
Let \(f(x) = \frac{{{{(\ln x)}^2}}}{2}\), for \(x > 0\).
Let \(g(x) = \frac{1}{x}\). The following diagram shows parts of the graphs of \(f’\) and g.
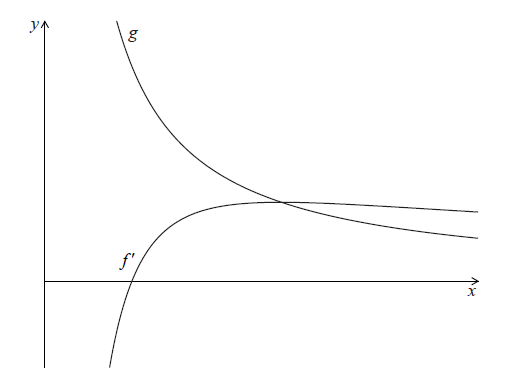
The graph of \(f’\) has an x-intercept at \(x = p\).
Show that \(f'(x) = \frac{{\ln x}}{x}\).
There is a minimum on the graph of \(f\). Find the \(x\)-coordinate of this minimum.
Write down the value of \(p\).
The graph of \(g\) intersects the graph of \(f’\) when \(x = q\).
Find the value of \(q\).
The graph of \(g\) intersects the graph of \(f’\) when \(x = q\).
Let \(R\) be the region enclosed by the graph of \(f’\), the graph of \(g\) and the line \(x = p\).
Show that the area of \(R\) is \(\frac{1}{2}\).
Answer/Explanation
Markscheme
METHOD 1
correct use of chain rule A1A1
eg \(\frac{{2\ln x}}{2} \times \frac{1}{x},{\text{ }}\frac{{2\ln x}}{{2x}}\)
Note: Award A1 for \(\frac{{2\ln x}}{{2x}}\), A1 for \( \times \frac{1}{x}\).
\(f'(x) = \frac{{\ln x}}{x}\) AG N0
[2 marks]
METHOD 2
correct substitution into quotient rule, with derivatives seen A1
eg \(\frac{{2 \times 2\ln x \times \frac{1}{x} – 0 \times {{(\ln x)}^2}}}{4}\)
correct working A1
eg \(\frac{{4\ln x \times \frac{1}{x}}}{4}\)
\(f'(x) = \frac{{\ln x}}{x}\) AG N0
[2 marks]
setting derivative \( = 0\) (M1)
eg \(f'(x) = 0,{\text{ }}\frac{{\ln x}}{x} = 0\)
correct working (A1)
eg \(\ln x = 0,{\text{ }}x = {{\text{e}}^0}\)
\(x = 1\) A1 N2
[3 marks]
intercept when \(f'(x) = 0\) (M1)
\(p = 1\) A1 N2
[2 marks]
equating functions (M1)
eg \(f’ = g,{\text{ }}\frac{{\ln x}}{x} = \frac{1}{x}\)
correct working (A1)
eg \(\ln x = 1\)
\(q = {\text{e (accept }}x = {\text{e)}}\) A1 N2
[3 marks]
evidence of integrating and subtracting functions (in any order, seen anywhere) (M1)
eg \(\int_q^e {\left( {\frac{1}{x} – \frac{{\ln x}}{x}} \right){\text{d}}x{\text{, }}\int {f’ – g} } \)
correct integration \(\ln x – \frac{{{{(\ln x)}^2}}}{2}\) A2
substituting limits into their integrated function and subtracting (in any order) (M1)
eg \((\ln {\text{e}} – \ln 1) – \left( {\frac{{{{(\ln {\text{e}})}^2}}}{2} – \frac{{{{(\ln 1)}^2}}}{2}} \right)\)
Note: Do not award M1 if the integrated function has only one term.
correct working A1
eg \((1 – 0) – \left( {\frac{1}{2} – 0} \right),{\text{ }}1 – \frac{1}{2}\)
\({\text{area}} = \frac{1}{2}\) AG N0
Notes: Candidates may work with two separate integrals, and only combine them at the end. Award marks in line with the markscheme.
[5 marks]
Question
Write down the value of
(i) \({\log _3}27\);
(ii) \({\log _8}\frac{1}{8}\);
(iii) \({\log _{16}}4\).
Hence, solve \({\log _3}27 + {\log _8}\frac{1}{8} – {\log _{16}}4 = {\log _4}x\).
Answer/Explanation
Markscheme
(i) \({\log _3}27 = 3\) A1 N1
[1 mark]
(ii) \({\log _8}\frac{1}{8} = – 1\) A1 N1
[1 mark]
(iii) \({\log _{16}}4 = \frac{1}{2}\) A1 N1
[1 mark]
correct equation with their three values (A1)
eg \(\frac{3}{2} = {\log _4}x{\text{, }}3 + ( – 1) – \frac{1}{2} = {\log _4}x\)
correct working involving powers (A1)
eg \(x = {4^{\frac{3}{2}}}{\text{, }}{4^{\frac{3}{2}}} = {4^{{{\log }_4}x}}\)
\(x = 8\) A1 N2
[3 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
Let \(f(x) = 3{x^2} – 6x + p\). The equation \(f(x) = 0\) has two equal roots.
Write down the value of the discriminant.
Hence, show that \(p = 3\).
The graph of \(f\)has its vertex on the \(x\)-axis.
Find the coordinates of the vertex of the graph of \(f\).
The graph of \(f\) has its vertex on the \(x\)-axis.
Write down the solution of \(f(x) = 0\).
The graph of \(f\) has its vertex on the \(x\)-axis.
The function can be written in the form \(f(x) = a{(x – h)^2} + k\). Write down the value of \(a\).
The graph of \(f\) has its vertex on the \(x\)-axis.
The function can be written in the form \(f(x) = a{(x – h)^2} + k\). Write down the value of \(h\).
The graph of \(f\) has its vertex on the \(x\)-axis.
The function can be written in the form \(f(x) = a{(x – h)^2} + k\). Write down the value of \(k\).
The graph of \(f\) has its vertex on the \(x\)-axis.
The graph of a function \(g\) is obtained from the graph of \(f\) by a reflection of \(f\) in the \(x\)-axis, followed by a translation by the vector \(\left( \begin{array}{c}0\\6\end{array} \right)\). Find \(g\), giving your answer in the form \(g(x) = A{x^2} + Bx + C\).
Answer/Explanation
Markscheme
correct value \(0\), or \(36 – 12p\) A2 N2
[2 marks]
correct equation which clearly leads to \(p = 3\) A1
eg \(36 – 12p = 0,{\text{ }}36 = 12p\)
\(p = 3\) AG N0
[1 mark]
METHOD 1
valid approach (M1)
eg \(x = – \frac{b}{{2a}}\)
correct working A1
eg \( – \frac{{( – 6)}}{{2(3)}},{\text{ }}x = \frac{6}{6}\)
correct answers A1A1 N2
eg \(x = 1,{\text{ }}y = 0;{\text{ }}(1,{\text{ }}0)\)
METHOD 2
valid approach (M1)
eg \(f(x) = 0\), factorisation, completing the square
correct working A1
eg \({x^2} – 2x + 1 = 0,{\text{ }}(3x – 3)(x – 1),{\text{ }}f(x) = 3{(x – 1)^2}\)
correct answers A1A1 N2
eg \(x = 1,{\text{ }}y = 0;{\text{ }}(1,{\text{ }}0)\)
METHOD 3
valid approach using derivative (M1)
eg \(f'(x) = 0,{\text{ }}6x – 6\)
correct equation A1
eg \(6x – 6 = 0\)
correct answers A1A1 N2
eg \(x = 1,{\text{ }}y = 0;{\text{ }}(1,{\text{ }}0)\)
[4 marks]
\(x = 1\) A1 N1
[1 mark]
\(a = 3\) A1 N1
[1 mark]
\(h = 1\) A1 N1
[1 mark]
\(k = 0\) A1 N1
[1 mark]
attempt to apply vertical reflection (M1)
eg \( – f(x),{\text{ }} – 3{(x – 1)^2}\), sketch
attempt to apply vertical shift 6 units up (M1)
eg \( – f(x) + 6\), vertex \((1, 6)\)
transformations performed correctly (in correct order) (A1)
eg \( – 3{(x – 1)^2} + 6,{\text{ }} – 3{x^2} + 6x – 3 + 6\)
\(g(x) = – 3{x^2} + 6x + 3\) A1 N3
[4 marks]
Question
Write the expression \(3\ln 2 – \ln 4\) in the form \(\ln k\), where \(k \in \mathbb{Z}\).
Hence or otherwise, solve \(3\ln 2 – \ln 4 = – \ln x\).
Answer/Explanation
Markscheme
correct application of \(\ln {a^b} = b\ln a\) (seen anywhere) (A1)
eg\(\;\;\;\ln 4 = 2\ln 2,{\text{ }}3\ln 2 = \ln {2^3},{\text{ }}3\log 2 = \log 8\)
correct working (A1)
eg\(\;\;\;3\ln 2 – 2\ln 2,{\text{ }}\ln 8 – \ln 4\)
\(\ln 2\;\;\;{\text{(accept }}k = 2{\text{)}}\) A1 N2
[3 marks]
METHOD 1
attempt to substitute their answer into the equation (M1)
eg\(\;\;\;\ln 2 = – \ln x\)
correct application of a log rule (A1)
eg\(\;\;\;\ln \frac{1}{x},{\text{ }}\ln \frac{1}{2} = \ln x,{\text{ }}\ln 2 + \ln x = \ln 2x\;\;\;( = 0)\)
\(x = \frac{1}{2}\) A1 N2
METHOD 2
attempt to rearrange equation, with \(3\ln 2\) written as \(\ln {2^3}\) or \(\ln 8\) (M1)
eg\(\;\;\;\ln x = \ln 4 – \ln {2^3},{\text{ }}\ln 8 + \ln x = \ln 4,{\text{ }}\ln {2^3} = \ln 4 – \ln x\)
correct working applying \(\ln a \pm \ln b\) (A1)
eg\(\;\;\;\frac{4}{8},{\text{ }}8x = 4,{\text{ }}\ln {2^3} = \ln \frac{4}{x}\)
\(x = \frac{1}{2}\) A1 N2
[3 marks]
Total [6 marks]
Question
Three consecutive terms of a geometric sequence are \(x – 3\), 6 and \(x + 2\).
Find the possible values of \(x\).
Answer/Explanation
Markscheme
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(r = \frac{6}{{x – 3}},{\text{ }}(x – 3) \times r = 6,{\text{ }}(x – 3){r^2} = x + 2\)
correct equation in terms of \(x\) only A1
eg\(\,\,\,\,\,\)\(\frac{6}{{x – 3}} = \frac{{x + 2}}{6},{\text{ }}(x – 3)(x + 2) = {6^2},{\text{ }}36 = {x^2} – x – 6\)
correct working (A1)
eg\(\,\,\,\,\,\)\({x^2} – x – 42,{\text{ }}{x^2} – x = 42\)
valid attempt to solve their quadratic equation (M1)
eg\(\,\,\,\,\,\)factorizing, formula, completing the square
evidence of correct working (A1)
eg\(\,\,\,\,\,\)\((x – 7)(x + 6),{\text{ }}\frac{{1 \pm \sqrt {169} }}{2}\)
\(x = 7,{\text{ }}x = – 6\) A1 N4
METHOD 2 (finding r first)
valid approach (M1)
eg\(\,\,\,\,\,\)\(r = \frac{6}{{x – 3}},{\text{ }}6r = x + 2,{\text{ }}(x – 3){r^2} = x + 2\)
correct equation in terms of \(r\) only A1
eg\(\,\,\,\,\,\)\(\frac{6}{r} + 3 = 6r – 2,{\text{ }}6 + 3r = 6{r^2} – 2r,{\text{ }}6{r^2} – 5r – 6 = 0\)
evidence of correct working (A1)
eg\(\,\,\,\,\,\)\((3r + 2)(2r – 3),{\text{ }}\frac{{5 \pm \sqrt {25 + 144} }}{{12}}\)
\(r = – \frac{2}{3},{\text{ }}r = \frac{3}{2}\) A1
substituting their values of \(r\) to find \(x\) (M1)
eg\(\,\,\,\,\,\)\((x – 3)\left( {\frac{2}{3}} \right) = 6,{\text{ }}x = 6\left( {\frac{3}{2}} \right) – 2\)
\(x = 7,{\text{ }}x = – 6\) A1 N4
[6 marks]
Question
Let \(f(x) = {x^2} – x\), for \(x \in \mathbb{R}\). The following diagram shows part of the graph of \(f\).
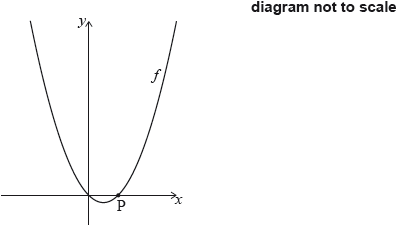
The graph of \(f\) crosses the \(x\)-axis at the origin and at the point \({\text{P}}(1,{\text{ }}0)\).
The line L is the normal to the graph of f at P.
The line \(L\) intersects the graph of \(f\) at another point Q, as shown in the following diagram.
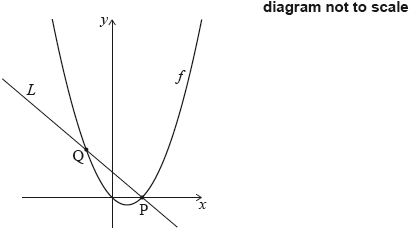
Show that \(f’(1) = 1\).
Find the equation of \(L\) in the form \(y = ax + b\).
Find the \(x\)-coordinate of Q.
Find the area of the region enclosed by the graph of \(f\) and the line \(L\).
Answer/Explanation
Markscheme
\(f’(x) = 2x – 1\) A1A1
correct substitution A1
eg\(\,\,\,\,\,\)\(2(1) – 1,{\text{ }}2 – 1\)
\(f’(1) = 1\) AG N0
[3 marks]
correct approach to find the gradient of the normal (A1)
eg\(\,\,\,\,\,\)\(\frac{{ – 1}}{{f'(1)}},{\text{ }}{m_1}{m_2} = – 1,{\text{ slope}} = – 1\)
attempt to substitute correct normal gradient and coordinates into equation of a line (M1)
eg\(\,\,\,\,\,\)\(y – 0 = – 1(x – 1),{\text{ }}0 = – 1 + b,{\text{ }}b = 1,{\text{ }}L = – x + 1\)
\(y = – x + 1\) A1 N2
[3 marks]
equating expressions (M1)
eg\(\,\,\,\,\,\)\(f(x) = L,{\text{ }} – x + 1 = {x^2} – x\)
correct working (must involve combining terms) (A1)
eg\(\,\,\,\,\,\)\({x^2} – 1 = 0,{\text{ }}{x^2} = 1,{\text{ }}x = 1\)
\(x = – 1\,\,\,\,\,\left( {{\text{accept }}Q( – 1,{\text{ }}2)} \right)\) A2 N3
[4 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(\int {L – f,{\text{ }}\int_{ – 1}^1 {(1 – {x^2}){\text{d}}x} } \), splitting area into triangles and integrals
correct integration (A1)(A1)
eg\(\,\,\,\,\,\)\(\left[ {x – \frac{{{x^3}}}{3}} \right]_{ – 1}^1,{\text{ }} – \frac{{{x^3}}}{3} – \frac{{{x^2}}}{2} + \frac{{{x^2}}}{2} + x\)
substituting their limits into their integrated function and subtracting (in any order) (M1)
eg\(\,\,\,\,\,\)\(1 – \frac{1}{3} – \left( { – 1 – \frac{{ – 1}}{3}} \right)\)
Note: Award M0 for substituting into original or differentiated function.
area \( = \frac{4}{3}\) A2 N3
[6 marks]
