Download IITian Academy App for accessing Online Mock Tests and More..
Question
The following graph shows the depth of water, y metres , at a point P, during one day. The time t is given in hours, from midnight to noon.
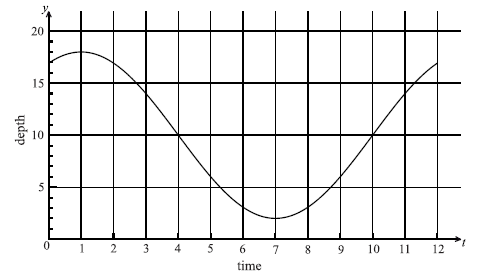
Use the graph to write down an estimate of the value of t when
(i) the depth of water is minimum;
(ii) the depth of water is maximum;
(iii) the depth of the water is increasing most rapidly.
The depth of water can be modelled by the function \(y = \cos A(B(t – 1)) + C\) .
(i) Show that \(A = 8\) .
(ii) Write down the value of C.
(iii) Find the value of B.
A sailor knows that he cannot sail past P when the depth of the water is less than 12 m . Calculate the values of t between which he cannot sail past P.
Answer/Explanation
Markscheme
(i) 7 A1 N1
(ii) 1 A1 N1
(iii) 10 A1 N1
[3 marks]
(i) evidence of appropriate approach M1
e.g. \(A = \frac{{18 – 2}}{2}\)
\(A = 8\) AG N0
(ii) \(C = 10\) A2 N2
(iii) METHOD 1
\({\text{period}} = 12\) (A1)
evidence of using \(B \times {\rm{period}} = 2\pi \) (accept \(360^\circ \) ) (M1)
e.g. \(12 = \frac{{2\pi }}{B}\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
METHOD 2
evidence of substituting (M1)
e.g. \(10 = 8\cos 3B + 10\)
simplifying (A1)
e.g. \(\cos 3B = 0\) \(\left( {3B = \frac{\pi }{2}} \right)\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
[6 marks]
correct answers A1A1
e.g. \(t = 3.52\) , \(t = 10.5\) , between 03:31 and 10:29 (accept 10:30) N2
[2 marks]
Question
Let \(f(x) = \frac{{3x}}{2} + 1\) , \(g(x) = 4\cos \left( {\frac{x}{3}} \right) – 1\) . Let \(h(x) = (g \circ f)(x)\) .
Find an expression for \(h(x)\) .
Write down the period of \(h\) .
Write down the range of \(h\) .
Answer/Explanation
Markscheme
attempt to form any composition (even if order is reversed) (M1)
correct composition \(h(x) = g\left( {\frac{{3x}}{2} + 1} \right)\) (A1)
\(h(x) = 4\cos \left( {\frac{{\frac{{3x}}{2} + 1}}{3}} \right) – 1\) \(\left( {4\cos \left( {\frac{1}{2}x + \frac{1}{3}} \right) – 1,4\cos \left( {\frac{{3x + 2}}{6}} \right) – 1} \right)\) A1 N3
[3 marks]
period is \(4\pi (12.6)\) A1 N1
[1 mark]
range is \( – 5 \le h(x) \le 3\) \(\left( {\left[ { – 5,3} \right]} \right)\) A1A1 N2
[2 marks]
Question
Let \(f(x) = 3\sin x + 4\cos x\) , for \( – 2\pi \le x \le 2\pi \) .
Sketch the graph of f .
Write down
(i) the amplitude;
(ii) the period;
(iii) the x-intercept that lies between \( – \frac{\pi }{2}\) and 0.
Hence write \(f(x)\) in the form \(p\sin (qx + r)\) .
Write down one value of x such that \(f'(x) = 0\) .
Write down the two values of k for which the equation \(f(x) = k\) has exactly two solutions.
Let \(g(x) = \ln (x + 1)\) , for \(0 \le x \le \pi \) . There is a value of x, between \(0\) and \(1\), for which the gradient of f is equal to the gradient of g. Find this value of x.
Answer/Explanation
Markscheme
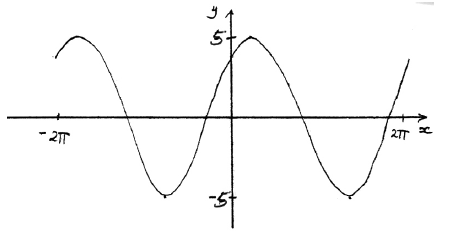A1A1A1 N3
Note: Award A1 for approximately sinusoidal shape, A1 for end points approximately correct \(( – 2\pi {\text{, }}4)\) \((2\pi {\text{, }}4)\), A1 for approximately correct position of graph, (y-intercept \((0{\text{, }}4)\), maximum to right of y-axis).
[3 marks]
(i) 5 A1 N1
(ii) \(2\pi \) (6.28) A1 N1
(iii) \( – 0.927\) A1 N1
[3 marks]
\(f(x) = 5\sin (x + 0.927)\) (accept \(p = 5\) , \(q = 1\) , \(r = 0.927\) ) A1A1A1 N3
[3 marks]
evidence of correct approach (M1)
e.g. max/min, sketch of \(f'(x)\) indicating roots
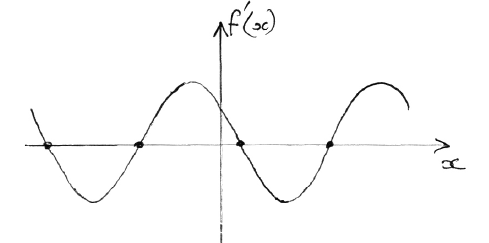
one 3 s.f. value which rounds to one of \( – 5.6\), \( – 2.5\), \(0.64\), \(3.8\) A1 N2
[2 marks]
\(k = – 5\) , \(k = 5\) A1A1 N2
[2 marks]
METHOD 1
graphical approach (but must involve derivative functions) M1
e.g.
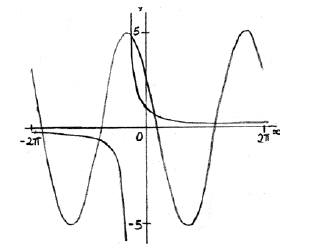
each curve A1A1
\(x = 0.511\) A2 N2
METHOD 2
\(g'(x) = \frac{1}{{x + 1}}\) A1
\(f'(x) = 3\cos x – 4\sin x\) \((5\cos (x + 0.927))\) A1
evidence of attempt to solve \(g'(x) = f'(x)\) M1
\(x = 0.511\) A2 N2
[5 marks]
Question
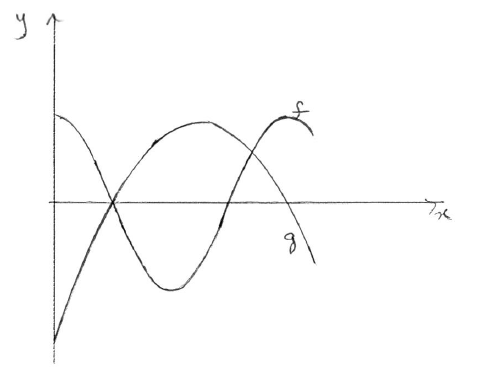
Let \(f(x) = 5\cos \frac{\pi }{4}x\) and \(g(x) = – 0.5{x^2} + 5x – 8\) for \(0 \le x \le 9\) .
On the same diagram, sketch the graphs of f and g .
Consider the graph of \(f\) . Write down
(i) the x-intercept that lies between \(x = 0\) and \(x = 3\) ;
(ii) the period;
(iii) the amplitude.
Consider the graph of g . Write down
(i) the two x-intercepts;
(ii) the equation of the axis of symmetry.
Let R be the region enclosed by the graphs of f and g . Find the area of R.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for f being of sinusoidal shape, with 2 maxima and one minimum, A1 for g being a parabola opening down, A1 for two intersection points in approximately correct position.
[3 marks]
(i) \((2{\text{, }}0)\) (accept \(x = 2\) ) A1 N1
(ii) \({\text{period}} = 8\) A2 N2
(iii) \({\text{amplitude}} = 5\) A1 N1
[4 marks]
(i) \((2{\text{, }}0)\) , \((8{\text{, }}0)\) (accept \(x = 2\) , \(x = 8\) ) A1A1 N1N1
(ii) \(x = 5\) (must be an equation) A1 N1
[3 marks]
METHOD 1
intersect when \(x = 2\) and \(x = 6.79\) (may be seen as limits of integration) A1A1
evidence of approach (M1)
e.g. \(\int {g – f} \) , \(\int {f(x){\rm{d}}x – \int {g(x){\rm{d}}x}}\) , \(\int_2^{6.79} {\left( {( – 0.5{x^2} + 5x – 8) – \left( {5\cos \frac{\pi }{4}x} \right)} \right)}\)
\({\text{area}} = 27.6\) A2 N3
METHOD 2
intersect when \(x = 2\) and \(x = 6.79\) (seen anywhere) A1A1
evidence of approach using a sketch of g and f , or \(g – f\) . (M1)
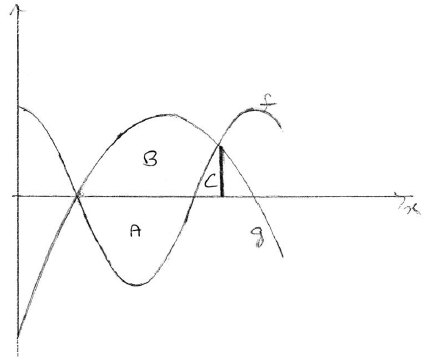
e.g. area = \(A + B – C\) , \(12.7324 + 16.0938 – 1.18129 \ldots \)
\({\text{area}} = 27.6\) A2 N3
[5 marks]
Question
The graph of \(y = p\cos qx + r\) , for \( – 5 \le x \le 14\) , is shown below.
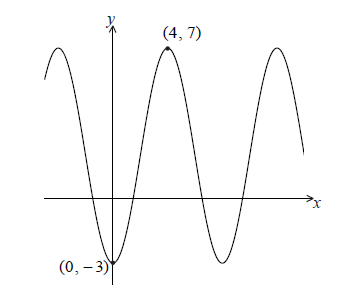
There is a minimum point at (0, −3) and a maximum point at (4, 7) .
Find the value of
(i) p ;
(ii) q ;
(iii) r.
The equation \(y = k\) has exactly two solutions. Write down the value of k.
Answer/Explanation
Markscheme
(i) evidence of finding the amplitude (M1)
e.g. \(\frac{{7 + 3}}{2}\) , amplitude \(= 5\)
\(p = – 5\) A1 N2
(ii) period \(= 8\) (A1)
\(q = 0.785\) \(\left( { = \frac{{2\pi }}{8} = \frac{\pi }{4}} \right)\) A1 N2
(iii) \(r = \frac{{7 – 3}}{2}\) (A1)
\(r = 2\) A1 N2
[6 marks]
\(k = – 3\) (accept \(y = – 3\) ) A1 N1
[1 mark]
Question
The following diagram represents a large Ferris wheel at an amusement park.
The points P, Q and R represent different positions of a seat on the wheel.
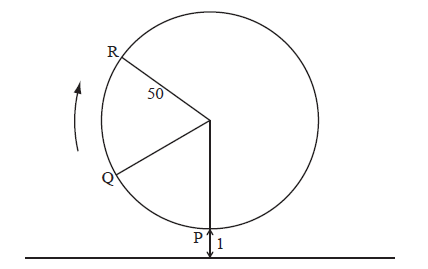
The wheel has a radius of 50 metres and rotates clockwise at a rate of one revolution every 30 minutes.
A seat starts at the lowest point P, when its height is one metre above the ground.
Find the height of a seat above the ground after 15 minutes.
After six minutes, the seat is at point Q. Find its height above the ground at Q.
The height of the seat above ground after t minutes can be modelled by the function \(h(t) = 50\sin (b(t – c)) + 51\).
Find the value of b and of c .
The height of the seat above ground after t minutes can be modelled by the function \(h(t) = 50\sin (b(t – c)) + 51\).
Hence find the value of t the first time the seat is \(96{\text{ m}}\) above the ground.
Answer/Explanation
Markscheme
valid approach (M1)
e.g. 15 mins is half way, top of the wheel, \(d + 1\)
height \( = 101\) (metres) A1 N2
[2 marks]
evidence of identifying rotation angle after 6 minutes A1
e.g. \(\frac{{2\pi }}{5}\) , \(\frac{1}{5}\) of a rotation, \({72^ \circ }\)
evidence of appropriate approach (M1)
e.g. drawing a right triangle and using cosine ratio
correct working (seen anywhere) A1
e.g. \(\cos \frac{{2\pi }}{5} = \frac{x}{{50}}\) , \(15.4(508 \ldots )\)
evidence of appropriate method M1
e.g. height \(= {\rm{radius}} + 1 – 15.45 \ldots \)
height \(= 35.5\) (metres) (accept 35.6) A1 N2
[5 marks]
METHOD 1
evidence of substituting into \(b = \frac{{2\pi }}{{{\rm{period}}}}\) (M1)
correct substitution
e.g. period = 30 minutes, \(b = \frac{{2\pi }}{{30}}\) A1
\(b = 0.209\) \(\left( {\frac{\pi }{{15}}} \right)\) A1 N2
substituting into \(h(t)\) (M1)
e.g. \(h(0) = 1\) , \(h(15) = 101\)
correct substitution A1
\(1 = 50\sin \left( { – \frac{\pi }{{15}}c} \right) + 51\)
\(c = 7.5\) A1 N2
METHOD 2
evidence of setting up a system of equations (M1)
two correct equations
e.g. \(1 = 50\sin b(0 – c) + 51\) , \(101 = 50\sin b(15 – c) + 51\) A1A1
attempt to solve simultaneously (M1)
e.g. evidence of combining two equations
\(b = 0.209\) \(\left( {\frac{\pi }{{15}}} \right)\) , \(c = 7.5\) A1A1 N2N2
[6 marks]
evidence of solving \(h(t) = 96\) (M1)
e.g. equation, graph
\(t = 12.8\) (minutes) A2 N3
[3 marks]
Question
The following diagram shows a waterwheel with a bucket. The wheel rotates at a constant rate in an anticlockwise (counter-clockwise) direction.
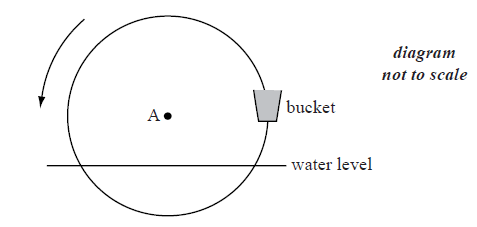
The diameter of the wheel is 8 metres. The centre of the wheel, A, is 2 metres above the water level. After t seconds, the height of the bucket above the water level is given by \(h = a\sin bt + 2\) .
Show that \(a = 4\) .
The wheel turns at a rate of one rotation every 30 seconds.
Show that \(b = \frac{\pi }{{15}}\) .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\) .
Find these values of t .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\) .
Determine whether the bucket is underwater at the second value of t .
Answer/Explanation
Markscheme
METHOD 1
evidence of recognizing the amplitude is the radius (M1)
e.g. amplitude is half the diameter
\(a = \frac{8}{2}\) A1
\(a = 4\) AG N0
METHOD 2
evidence of recognizing the maximum height (M1)
e.g. \(h = 6\) , \(a\sin bt + 2 = 6\)
correct reasoning
e.g. \(a\sin bt = 4\) and \(\sin bt\) has amplitude of 1 A1
\(a = 4\) AG N0
[2 marks]
METHOD 1
period = 30 (A1)
\(b = \frac{{2\pi }}{{30}}\) A1
\(b = \frac{\pi }{{15}}\) AG N0
METHOD 2
correct equation (A1)
e.g. \(2 = 4\sin 30b + 2\) , \(\sin 30b = 0\)
\(30b = 2\pi \) A1
\(b = \frac{\pi }{{15}}\) AG N0
[2 marks]
recognizing \(h'(t) = – 0.5\) (seen anywhere) R1
attempting to solve (M1)
e.g. sketch of \(h’\) , finding \(h’\)
correct work involving \(h’\) A2
e.g. sketch of \(h’\) showing intersection, \( – 0.5 = \frac{{4\pi }}{{15}}\cos \left( {\frac{\pi }{{15}}t} \right)\)
\(t = 10.6\) , \(t = 19.4\) A1A1 N3
[6 marks]
METHOD 1
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of substituting into h (M1)
e.g. \(h(19.4)\) , \(4\sin \frac{{19.4\pi }}{{15}} + 2\)
correct calculation A1
e.g. \(h(19.4) = – 1.19\)
correct statement A1 N0
e.g. the bucket is underwater, yes
METHOD 2
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of valid approach (M1)
e.g. solving \(h(t) = 0\) , graph showing region below x-axis
correct roots A1
e.g. \(17.5\), \(27.5\)
correct statement A1 N0
e.g. the bucket is underwater, yes
[4 marks]
Question
A Ferris wheel with diameter \(122\) metres rotates clockwise at a constant speed. The wheel completes \(2.4\) rotations every hour. The bottom of the wheel is \(13\) metres above the ground.
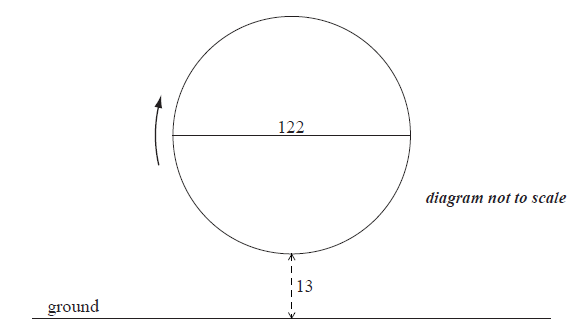
A seat starts at the bottom of the wheel.
After t minutes, the height \(h\) metres above the ground of the seat is given by\[h = 74 + a\cos bt {\rm{ .}}\]
Find the maximum height above the ground of the seat.
(i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(b) (i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(c) Find the value of \(a\) .
(d) Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
Find the value of \(a\) .
Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
In one rotation of the wheel, find the probability that a randomly selected seat is at least \(105\) metres above the ground.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(13 + {\rm{diameter}}\) , \(13 + 122\)
maximum height \( = 135\) (m) A1 N2
[2 marks]
(i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(a) (i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(b) METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
(c)
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
Total [9 marks]
METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
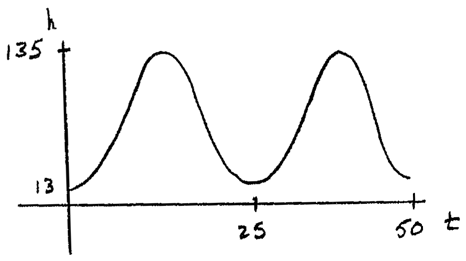A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
setting up inequality (accept equation) (M1)
eg \(h > 105\) , \(105 = 74 + a\cos bt\) , sketch of graph with line \(y = 105\)
any two correct values for t (seen anywhere) A1A1
eg \(t = 8.371 \ldots \) , \(t = 16.628 \ldots \) , \(t = 33.371 \ldots \) , \(t = 41.628 \ldots \)
valid approach M1
eg \(\frac{{16.628 – 8.371}}{{25}}\) , \(\frac{{{t_1} – {t_2}}}{{25}}\) , \(\frac{{2 \times 8.257}}{{50}}\) , \(\frac{{2(12.5 – 8.371)}}{{25}}\)
\(p = 0.330\) A1 N2
[5 marks]
Question
Let \(f(x) = p\cos \left( {q(x + r)} \right) + 10\), for \(0 \leqslant x \leqslant 20\). The following diagram shows the graph of \(f\).
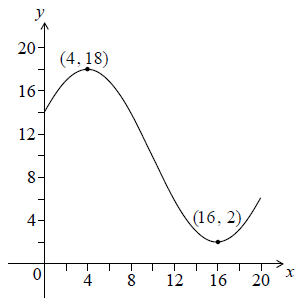
The graph has a maximum at \((4, 18)\) and a minimum at \((16, 2)\).
Write down the value of \(r\).
Find \(p\).
Find \(q\).
Solve \(f(x) = 7\).
Answer/Explanation
Markscheme
\(r = – 4\) A2 N2
Note: Award A1 for \(r = 4\).
[2 marks]
evidence of valid approach (M1)
eg \(\frac{{\max y{\text{ value — }}y{\text{ value}}}}{2}\), distance from \(y = 10\)
\(p = 8\) A1 N2
[2 marks]
valid approach (M1)
eg period is \(24\), \(\frac{{360}}{{24}}\), substitute a point into their \(f(x)\)
\(q = \frac{{2\pi }}{{24}}\left( {\frac{\pi }{{12}},{\text{ exact}}} \right)\), \(0.262\) (do not accept degrees) A1 N2
[2 marks]
valid approach (M1)
eg line on graph at \(y = 7,{\text{ }}8\cos \left( {\frac{{2\pi }}{{24}}(x – 4)} \right) + 10 = 7\)
\(x = 11.46828\)
\(x = 11.5\) (accept \((11.5, 7)\)) A1 N2
[2 marks]
Note: Do not award the final A1 if additional values are given. If an incorrect value of \(q\) leads to multiple solutions, award the final A1 only if all solutions within the domain are given.
Question
The following diagram shows part of the graph of \(y = p\sin (qx) + r\).
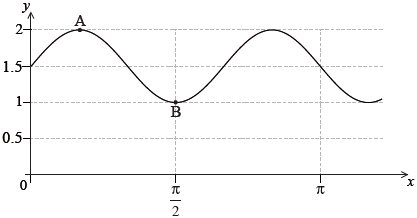
The point \({\text{A}}\left( {\frac{\pi }{6},{\text{ }}2} \right)\) is a maximum point and the point \({\text{B}}\left( {\frac{\pi }{6},{\text{ }}1} \right)\) is a minimum point.
Find the value of
\(p\);
\(r\);
\(q\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\;\;\;\)\(\frac{{2 – 1}}{2},{\text{ }}2 – 1.5\)
\(p = 0.5\) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;\)\(\frac{{1 + 2}}{2}\)
\(r = 1.5\) A1 N2
[2 marks]
METHOD 1
valid approach (seen anywhere) M1
eg\(\;\;\;\)\(q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{\left( {\frac{{2\pi }}{3}} \right)}}\)
period \( = \frac{{2\pi }}{3}\)\(\;\;\;\)(seen anywhere) (A1)
\(q = 3\) A1 N2
METHOD 2
attempt to substitute one point and their values for \(p\) and \(r\) into \(y\) M1
eg\(\;\;\;\)\(2 = 0.5\sin \left( {q\frac{\pi }{6}} \right) + 1.5,{\text{ }}\frac{\pi }{2} = 0.5\sin (q1) + 1.5\)
correct equation in \(q\) (A1)
eg\(\;\;\;\)\(q\frac{\pi }{6} = \frac{\pi }{2},{\text{ }}q\frac{\pi }{2} = \frac{{3\pi }}{2}\)
\(q = 3\) A1 N2
METHOD 3
valid reasoning comparing the graph with that of \(\sin x\) R1
eg\(\;\;\;\)position of max/min, graph goes faster
correct working (A1)
eg\(\;\;\;\)max at \(\frac{\pi }{6}\) not at \(\frac{\pi }{2}\), graph goes \(3\) times as fast
\(q = 3\) A1 N2
[3 marks]
Total [7 marks]
Question
The following diagram shows the graph of \(f(x) = a\sin bx + c\), for \(0 \leqslant x \leqslant 12\).
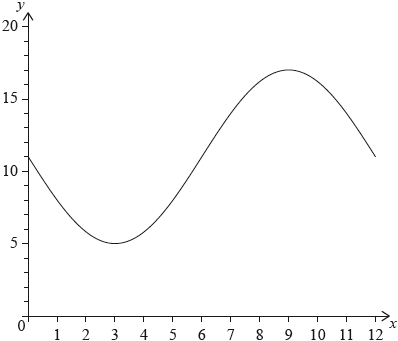
The graph of \(f\) has a minimum point at \((3,{\text{ }}5)\) and a maximum point at \((9,{\text{ }}17)\).
The graph of \(g\) is obtained from the graph of \(f\) by a translation of \(\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)\). The maximum point on the graph of \(g\) has coordinates \((11.5,{\text{ }}17)\).
The graph of \(g\) changes from concave-up to concave-down when \(x = w\).
(i) Find the value of \(c\).
(ii) Show that \(b = \frac{\pi }{6}\).
(iii) Find the value of \(a\).
(i) Write down the value of \(k\).
(ii) Find \(g(x)\).
(i) Find \(w\).
(ii) Hence or otherwise, find the maximum positive rate of change of \(g\).
Answer/Explanation
Markscheme
(i) valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{5 + 17}}{2}\)
\(c = 11\) A1 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)period is 12, per \( = \frac{{2\pi }}{b},{\text{ }}9 – 3\)
\(b = \frac{{2\pi }}{{12}}\) A1
\(b = \frac{\pi }{6}\) AG N0
(iii) METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11\), substitution of points
\(a = – 6\) A1 N2
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{17 – 5}}{2}\), amplitude is 6
\(a = – 6\) A1 N2
[6 marks]
(i) \(k = 2.5\) A1 N1
(ii) \(g(x) = – 6\sin \left( {\frac{\pi }{6}(x – 2.5)} \right) + 11\) A2 N2
[3 marks]
(i) METHOD 1 Using \(g\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(g”(x) = 0\), sketch, coordinates of max/min on \({g’}\)
\(w = 8.5\) (exact) A1 N2
METHOD 2 Using \(f\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach involving translation (M1)
eg\(\,\,\,\,\,\)\(x = w – k\), sketch, \(6 + 2.5\)
\(w = 8.5\) (exact) A1 N2
(ii) valid approach involving the derivative of \(g\) or \(f\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(g'(w),{\text{ }} – \pi \cos \left( {\frac{\pi }{6}x} \right)\), max on derivative, sketch of derivative
attempt to find max value on derivative M1
eg\(\,\,\,\,\,\)\( – \pi \cos \left( {\frac{\pi }{6}(8.5 – 2.5)} \right),{\text{ }}f'(6)\), dot on max of sketch
3.14159
max rate of change \( = \pi \) (exact), 3.14 A1 N2
[6 marks]
Question
The depth of water in a port is modelled by the function \(d(t) = p\cos qt + 7.5\), for \(0 \leqslant t \leqslant 12\), where \(t\) is the number of hours after high tide.
At high tide, the depth is 9.7 metres.
At low tide, which is 7 hours later, the depth is 5.3 metres.
Find the value of \(p\).
Find the value of \(q\).
Use the model to find the depth of the water 10 hours after high tide.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} – {\text{min}}}}{2}\), sketch of graph, \(9.7 = p\cos (0) + 7.5\)
\(p = 2.2\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(B = \frac{{2\pi }}{{{\text{period}}}}\), period is \(14,{\text{ }}\frac{{360}}{{14}},{\text{ }}5.3 = 2.2\cos 7q + 7.5\)
0.448798
\(q = \frac{{2\pi }}{{14}}{\text{ }}\left( {\frac{\pi }{7}} \right)\), (do not accept degrees) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(d(10),{\text{ }}2.2\cos \left( {\frac{{20\pi }}{{14}}} \right) + 7.5\)
7.01045
7.01 (m) A1 N2
[2 marks]
Question
Let \(f\left( x \right) = 12\,\,{\text{cos}}\,x – 5\,\,{\text{sin}}\,x,\,\, – \pi \leqslant x \leqslant 2\pi \), be a periodic function with \(f\left( x \right) = f\left( {x + 2\pi } \right)\)
The following diagram shows the graph of \(f\).
There is a maximum point at A. The minimum value of \(f\) is −13 .
A ball on a spring is attached to a fixed point O. The ball is then pulled down and released, so that it moves back and forth vertically.
The distance, d centimetres, of the centre of the ball from O at time t seconds, is given by
\(d\left( t \right) = f\left( t \right) + 17,\,\,0 \leqslant t \leqslant 5.\)
Find the coordinates of A.
For the graph of \(f\), write down the amplitude.
For the graph of \(f\), write down the period.
Hence, write \(f\left( x \right)\) in the form \(p\,\,{\text{cos}}\,\left( {x + r} \right)\).
Find the maximum speed of the ball.
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
Answer/Explanation
Markscheme
−0.394791,13
A(−0.395, 13) A1A1 N2
[2 marks]
13 A1 N1
[1 mark]
\({2\pi }\), 6.28 A1 N1
[1 mark]
valid approach (M1)
eg recognizing that amplitude is p or shift is r
\(f\left( x \right) = 13\,\,{\text{cos}}\,\left( {x + 0.395} \right)\) (accept p = 13, r = 0.395) A1A1 N3
Note: Accept any value of r of the form \(0.395 + 2\pi k,\,\,k \in \mathbb{Z}\)
[3 marks]
recognizing need for d ′(t) (M1)
eg −12 sin(t) − 5 cos(t)
correct approach (accept any variable for t) (A1)
eg −13 sin(t + 0.395), sketch of d′, (1.18, −13), t = 4.32
maximum speed = 13 (cms−1) A1 N2
[3 marks]
recognizing that acceleration is needed (M1)
eg a(t), d ”(t)
correct equation (accept any variable for t) (A1)
eg \(a\left( t \right) = – 2,\,\,\left| {\frac{{\text{d}}}{{{\text{d}}t}}\left( {d’\left( t \right)} \right)} \right| = 2,\,\, – 12\,\,{\text{cos}}\,\left( t \right) + 5\,\,{\text{sin}}\,\left( t \right) = – 2\)
valid attempt to solve their equation (M1)
eg sketch, 1.33
1.02154
1.02 A2 N3
[5 marks]