Question
The following diagram shows triangle ABC, with AB = 10 , BC = x and AC = 2x .
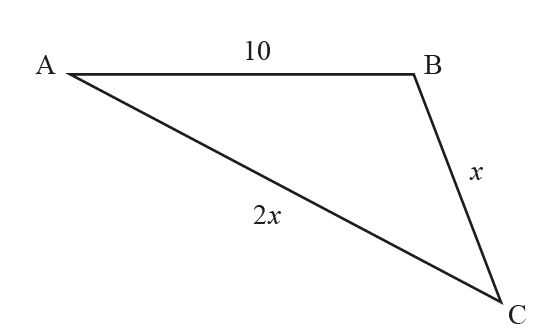
Given that cos\(\hat{C}\)=\(\frac{3}{4}\) , find the area of the triangle. Give your answer in the form \(\frac{p\sqrt{q}}{2}\) where p , q ∈ \(\mathbb{Z}^+\)
Answer/Explanation
Ans:
Let F be the foot of perpendicular of B on AC
Consider △BCF, since cos\(\hat{C}\)=\(\frac{3}{4}\), we have
\(\frac{\text{CF}}{x} = \frac{3}{4}\)
\(\text{CF} = \frac{3}{4}x.\)
Also, by Pythagoras’ Theorem, we have \(\text{BF}=\sqrt{x^2-\left(\frac{3}{4}x\right)^2}\), i.e., \(\text{BF}=\frac{\sqrt{7}}{4}x\).
Since \(\text{AC}=2x\), \(\text{AF}=\frac{5}{4}x\).
Consider \(\triangle\text{ABF}\), by Pythagoras’ Theorem, we have
\(10^2 = \left(\frac{\sqrt{7}}{4}x\right)^2 + \left(\frac{5}{4}x\right)^2 \)
\(2x^2 = 100
x^2 = 50. \)
Thus, we have
\(\text{area of }\triangle\text{ABC} = \frac{1}{2}\times 2x\times \frac{\sqrt{7}}{4}x \)
= \(\frac{\sqrt{7}}{4}x^2 \)
= \(\frac{50\sqrt{7}}{4} \)
= \(\frac{25\sqrt{7}}{2} \)
Question
The diagram shows a tangent, (TP) , to the circle with centre O and radius r . The size of \({\rm{P\hat OA}}\) is \(\theta \) radians.
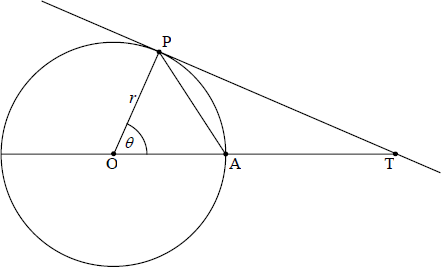
Find the area of triangle AOP in terms of r and \(\theta \) .[1]
Find the area of triangle POT in terms of r and \(\theta \) .[2]
Using your results from part (a) and part (b), show that \(\sin \theta < \theta < \tan \theta \) .[2]
Answer/Explanation
Markscheme
area of \({\text{AOP}} = \frac{1}{2}{r^2}\sin \theta \) A1
[1 mark]
\({\text{TP}} = r\tan \theta \) (M1)
area of POT \( = \frac{1}{2}r(r\tan \theta )\)
\( = \frac{1}{2}{r^2}\tan \theta \) A1
[2 marks]
area of sector OAP \( = \frac{1}{2}{r^2}\theta \) A1
area of triangle OAP < area of sector OAP < area of triangle POT R1
\(\frac{1}{2}{r^2}\sin \theta < \frac{1}{2}{r^2}\theta < \frac{1}{2}{r^2}\tan \theta \)
\(\sin \theta < \theta < \tan \theta \) AG
[2 marks]
Question
The diagram shows a tangent, (TP) , to the circle with centre O and radius r . The size of \({\rm{P\hat OA}}\) is \(\theta \) radians.
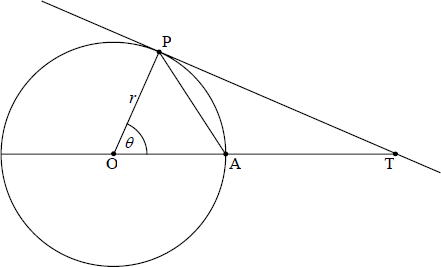
Find the area of triangle AOP in terms of r and \(\theta \) .[1]
Find the area of triangle POT in terms of r and \(\theta \) .[2]
Using your results from part (a) and part (b), show that \(\sin \theta < \theta < \tan \theta \) .[2]
Answer/Explanation
Markscheme
area of \({\text{AOP}} = \frac{1}{2}{r^2}\sin \theta \) A1
[1 mark]
\({\text{TP}} = r\tan \theta \) (M1)
area of POT \( = \frac{1}{2}r(r\tan \theta )\)
\( = \frac{1}{2}{r^2}\tan \theta \) A1
[2 marks]
area of sector OAP \( = \frac{1}{2}{r^2}\theta \) A1
area of triangle OAP < area of sector OAP < area of triangle POT R1
\(\frac{1}{2}{r^2}\sin \theta < \frac{1}{2}{r^2}\theta < \frac{1}{2}{r^2}\tan \theta \)
\(\sin \theta < \theta < \tan \theta \) AG
[2 marks]
Question
In the triangle PQR, PQ = 6 , PR = k and \({\rm{P\hat QR}} = 30^\circ \) .
For the case k = 4 , find the two possible values of QR.[4]
Determine the values of k for which the conditions above define a unique triangle.[3]
Answer/Explanation
Markscheme
attempt to apply cosine rule M1
\({4^2} = {6^2} + {\text{Q}}{{\text{R}}^2} – 2 \cdot {\text{QR}} \cdot 6\cos 30^\circ\) ( or \({\text{Q}}{{\text{R}}^2} – 6\sqrt 3 {\text{ QR}} + 20 = 0\) ) A1
\({\text{QR}} = 3\sqrt 3 + \sqrt 7 {\text{ or QR}} = 3\sqrt 3 – \sqrt 7 \) A1A1
[4 marks]
METHOD 1
\(k \geqslant 6\) A1
\(k = 6\sin 30^\circ = 3\) M1A1
Note: The M1 in (b) is for recognizing the right-angled triangle case.
METHOD 2
\(k \geqslant 6\) A1
use of discriminant: \(108 – 4(36 – {k^2}) = 0\) M1
k = 3 A1
Note: k = ±3 is M1A0.
[3 marks]
Question
The following diagram shows the triangle ABC where \({\text{AB}} = 2,{\text{ AC}} = \sqrt 2 \) and \({\rm{B\hat AC}} = 15^\circ \).
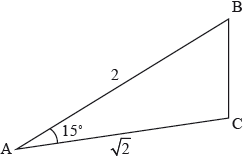
Expand and simplify \({\left( {1 – \sqrt 3 } \right)^2}\).[1]
By writing \(15^\circ \) as \(60^\circ – 45^\circ \) find the value of \(\cos (15^\circ )\).[3]
Find BC in the form \(a + \sqrt b \) where \(a,{\text{ }}b \in \mathbb{Z}\).[4]
Answer/Explanation
Markscheme
\({\left( {1 – \sqrt 3 } \right)^2} = 4 – 2\sqrt 3 \) A1
Note: Award A0 for \(1 – 2\sqrt 3 + 3\).
[1 mark]
\(\cos (60^\circ – 45^\circ ) = \cos (60^\circ )\cos (45^\circ ) + \sin (60^\circ )\sin (45^\circ )\) M1
\( = \frac{1}{2} \times \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 2 }}{2}{\text{ }}\left( {{\text{or }}\frac{1}{2} \times \frac{1}{{\sqrt 2 }} + \frac{{\sqrt 3 }}{2} \times \frac{1}{{\sqrt 2 }}} \right)\) (A1)
\( = \frac{{\sqrt 2 + \sqrt 6 }}{4}{\text{ }}\left( {{\text{or }}\frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}} \right)\) A1
[3 marks]
\(B{C^2} = 2 + 4 – 2 \times \sqrt 2 \times 2\cos (15^\circ )\) M1
\( = 6 – \sqrt 2 \left( {\sqrt 2 + \sqrt 6 } \right)\)
\( = 4 – \sqrt {12} {\text{ }}\left( { = 4 – 2\sqrt 3 } \right)\) A1
\(BC = \pm \left( {1 – \sqrt 3 } \right)\) (M1)
\(BC = – 1 + \sqrt 3 \) A1
Note: Accept \(BC = \sqrt 3 – 1\).
Note: Award M1A0 for \(1 – \sqrt 3 \).
Note: Valid geometrical methods may be seen.
[4 marks]