Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \({\boldsymbol{v}} = 3{\boldsymbol{i}} + 4{\boldsymbol{j}} + {\boldsymbol{k}}\) and \({\boldsymbol{w}} = {\boldsymbol{i}} + 2{\boldsymbol{j}} – 3{\boldsymbol{k}}\) . The vector \({\boldsymbol{v}} + p{\boldsymbol{w}}\) is perpendicular to w. Find the value of p.
Answer/Explanation
Markscheme
\(p{\boldsymbol{w}} = p{\boldsymbol{i}} + 2p{\boldsymbol{j}} – 3p{\boldsymbol{k}}\) (seen anywhere) (A1)
attempt to find \({\boldsymbol{v}} + p{\boldsymbol{w}}\) (M1)
e.g. \(3{\boldsymbol{i}} + 4{\boldsymbol{j}} + {\boldsymbol{k}} + p({\boldsymbol{i}} + 2{\boldsymbol{j}} – 3{\boldsymbol{k}})\)
collecting terms \((3 + p){\boldsymbol{i}} + (4 + 2p){\boldsymbol{j}} + (1 – 3p){\boldsymbol{k}}\) A1
attempt to find the dot product (M1)
e.g. \(1(3 + p) + 2(4 + 2p) – 3(1 – 3p)\)
setting their dot product equal to 0 (M1)
e.g. \(1(3 + p) + 2(4 + 2p) – 3(1 – 3p) = 0\)
simplifying A1
e.g. \(3 + p + 8 + 4p – 3 + 9p = 0\) , \(14p + 8 = 0\)
\(p = – 0.571\) \(\left( { – \frac{8}{{14}}} \right)\) A1 N3
[7 marks]
Question
Consider the lines \({L_1}\) and \({L_2}\) with equations \({L_1}\) : \(\boldsymbol{r}=\left( \begin{array}{c}11\\8\\2\end{array} \right) + s\left( \begin{array}{c}4\\3\\ – 1\end{array} \right)\) and \({L_2}\) : \(\boldsymbol{r} = \left( \begin{array}{c}1\\1\\ – 7\end{array} \right) + t\left( \begin{array}{c}2\\1\\11\end{array} \right)\).
The lines intersect at point \(\rm{P}\).
Find the coordinates of \({\text{P}}\).
Show that the lines are perpendicular.
The point \({\text{Q}}(7, 5, 3)\) lies on \({L_1}\). The point \({\text{R}}\) is the reflection of \({\text{Q}}\) in the line \({L_2}\).
Find the coordinates of \({\text{R}}\).
Answer/Explanation
Markscheme
appropriate approach (M1)
eg \(\left( \begin{array}{c}11\\8\\2\end{array} \right) + s\left( \begin{array}{c}4\\3\\ – 1\end{array} \right) = \left( \begin{array}{c}1\\1\\ – 7\end{array} \right) + t\left( \begin{array}{c}2\\1\\11\end{array} \right)\), \({L_1} = {L_2}\)
any two correct equations A1A1
eg \(11 + 4s = 1 + 2t,{\text{ }}8 + 3s = 1 + t,{\text{ }}2 – s = – 7 + 11t\)
attempt to solve system of equations (M1)
eg \(10 + 4s = 2(7 + 3s), \left\{ {\begin{array}{*{20}{c}} {4s – 2t = – 10} \\ {3s – t = – 7} \end{array}} \right.\)
one correct parameter A1
eg \(s = – 2,{\text{ }}t = 1\)
\({\text{P}}(3, 2, 4)\) (accept position vector) A1 N3
[6 marks]
choosing correct direction vectors for \({L_1}\) and \({L_2}\) (A1)(A1)
eg \(\left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right),\left( {\begin{array}{*{20}{c}} 2 \\ 1 \\ {11} \end{array}} \right)\) (or any scalar multiple)
evidence of scalar product (with any vectors) (M1)
eg \(a \cdot b\), \(\left( \begin{array}{c}4\\3\\ – 1\end{array} \right) \bullet \left( \begin{array}{c}2\\1\\11\end{array} \right)\)
correct substitution A1
eg \(4(2) + 3(1) + ( – 1)(11),{\text{ }}8 + 3 – 11\)
calculating \(a \cdot b = 0\) A1
Note: Do not award the final A1 without evidence of calculation.
vectors are perpendicular AG N0
[5 marks]
Note: Candidates may take different approaches, which do not necessarily involve vectors.
In particular, most of the working could be done on a diagram. Award marks in line with the markscheme.
METHOD 1
attempt to find \(\overrightarrow {{\text{QP}}} \) or \(\overrightarrow {{\text{PQ}}} \) (M1)
correct working (may be seen on diagram) A1
eg \(\overrightarrow {{\text{QP}}} \) = \(\left( \begin{array}{c} – 4\\ – 3\\1\end{array} \right)\), \(\overrightarrow {{\text{PQ}}} \) = \(\left( \begin{array}{c}7\\5\\3\end{array} \right) – \left( \begin{array}{c}3\\2\\4\end{array} \right)\)
recognizing \({\text{R}}\) is on \({L_1}\) (seen anywhere) (R1)
eg on diagram
\({\text{Q}}\) and \({\text{R}}\) are equidistant from \({\text{P}}\) (seen anywhere) (R1)
eg \(\overrightarrow {{\text{QP}}} = \overrightarrow {{\text{PR}}} \), marked on diagram
correct working (A1)
eg \(\left( \begin{array}{c}3\\2\\4\end{array} \right) – \left( \begin{array}{c}7\\5\\3\end{array} \right) = \left( \begin{array}{c}x\\y\\z\end{array} \right) – \left( \begin{array}{c}3\\2\\4\end{array} \right),\left( \begin{array}{c} – 4\\ – 3\\1\end{array} \right) + \left( \begin{array}{c}3\\2\\4\end{array} \right)\)
\({\text{R}}(–1, –1, 5)\) (accept position vector) A1 N3
METHOD 2
recognizing \({\text{R}}\) is on \({L_1}\) (seen anywhere) (R1)
eg on diagram
\({\text{Q}}\) and \({\text{R}}\) are equidistant from \({\text{P}}\) (seen anywhere) (R1)
eg \({\text{P}}\) midpoint of \({\text{QR}}\), marked on diagram
valid approach to find one coordinate of mid-point (M1)
eg \({x_p} = \frac{{{x_Q} + {x_R}}}{2},{\text{ }}2{y_p} = {y_Q} + {y_R},{\text{ }}\frac{1}{2}\left( {{z_Q} + {z_R}} \right)\)
one correct substitution A1
eg \({x_R} = 3 + (3 – 7),{\text{ }}2 = \frac{{5 + {y_R}}}{2},{\text{ }}4 = \frac{1}{2}(z + 3)\)
correct working for one coordinate (A1)
eg \({x_R} = 3 – 4,{\text{ }}4 – 5 = {y_R},{\text{ }}8 = (z + 3)\)
\({\text{R}} (-1, -1, 5)\) (accept position vector) A1 N3
[6 marks]
Question
The following diagram shows two perpendicular vectors u and v.
Let \(w = u – v\). Represent \(w\) on the diagram above.
Given that \(u = \left( \begin{array}{c}3\\2\\1\end{array} \right)\) and \(v = \left( \begin{array}{c}5\\n\\3\end{array} \right)\), where \(n \in \mathbb{Z}\), find \(n\).
Answer/Explanation
Markscheme
METHOD 1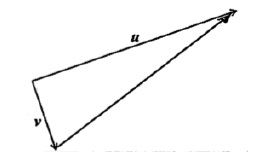
A1A1 N2
Note: Award A1 for segment connecting endpoints and A1 for direction (must see arrow).
METHOD 2
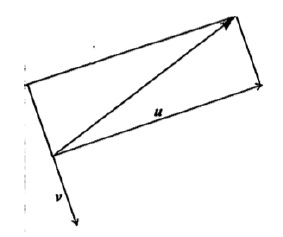A1A1 N2
Notes: Award A1 for segment connecting endpoints and A1 for direction (must see arrow).
Additional lines not required.
[2 marks]
evidence of setting scalar product equal to zero (seen anywhere) R1
eg u \( \cdot \) v \( = 0,{\text{ }}15 + 2n + 3 = 0\)
correct expression for scalar product (A1)
eg \(3 \times 5 + 2 \times n + 1 \times 3,{\text{ }}2n + 18 = 0\)
attempt to solve equation (M1)
eg \(2n = – 18\)
\(n = – 9\) A1 N3
[4 marks]
Question
Consider the lines \({L_1}\) , \({L_2}\) , \({L_2}\) , and \({L_4}\) , with respective equations.
\({L_1}\) : \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1\\
2\\
3
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
3\\
{ – 2}\\
1
\end{array}} \right)\)
\({L_2}\) : \(\left( \begin{array}{l}
x\\
y\\
z
\end{array} \right) = \left( \begin{array}{l}
1\\
2\\
3
\end{array} \right) + p\left( \begin{array}{l}
3\\
2\\
1
\end{array} \right)\)
\({L_3}\) : \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
0\\
1\\
0
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
{ – a}
\end{array}} \right)\)
\({L_4}\) : \(\left( {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right) = q\left( {\begin{array}{*{20}{c}}
{ – 6}\\
4\\
{ – 2}
\end{array}} \right)\)
Write down the line that is parallel to \({L_4}\) .
Write down the position vector of the point of intersection of \({L_1}\) and \({L_2}\) .
Given that \({L_1}\) is perpendicular to \({L_3}\) , find the value of a .
Answer/Explanation
Markscheme
\({L_1}\) A1 N1
[1 mark]
\(\left( \begin{array}{l}
1\\
2\\
3
\end{array} \right)\) A1 N1
[1 mark]
choosing correct direction vectors A1A1
e.g. \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 2}\\
1
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
{ – 1}\\
2\\
{ – a}
\end{array}} \right)\)
recognizing that \({\boldsymbol{a}} \bullet {\boldsymbol{b}} = 0\) M1
correct substitution A1
e.g. \( – 3 – 4 – a = 0\)
\(a = – 7\) A1 N3
[5 marks]