Question
[Maximum mark: 5] [without GDC]
The following results give the heights of sunflowers in centimetres.
180 184 195 177 175 173 169 167 197 173 166 183 161 195 177
192 161 165
Represent the data by a stem and leaf diagram.
Answer/Explanation
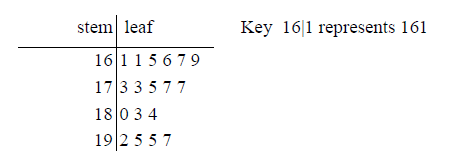
Question
[Maximum mark: 12] [without GDC]
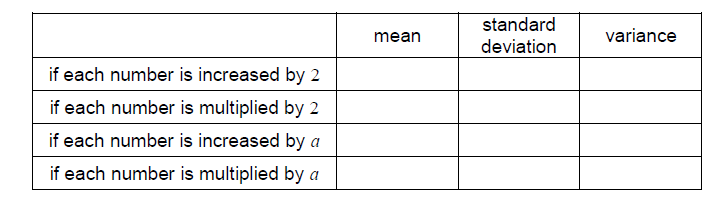
Consider the data 10, 20, 30, 40 with
mean = 25 standard deviation = \(5\sqrt{5}\) variance = 125
Find the new mean, standard deviation and variance in the following cases
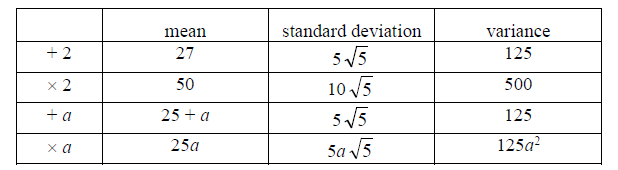
Answer/Explanation
mean = 25 standard deviation = \(5\sqrt{5}\) variance = 125
Question
[Maximum mark: 4] [without GDC]
The mean of the population x1, x2, … , x25 is \(m\)
(a) Given that \(\sum_{i=1}^{25}x_{i}=300\) find the value of \(m\) .
(b) Given that \(m\) = 10 find the value of \(\sum_{i=1}^{25}x_{i}\).
Answer/Explanation
(a) m = \(\frac{300}{25}=12\)
(b) \(\sum_{i=1}^{25}x_{i}=25×10=250\);
Question
[Maximum mark: 6] [without GDC]
The table below shows the marks gained in a test by a group of students.

The median is 3 and the mode is 2. Find the two possible values of \(p\).
Answer/Explanation
List of frequencies with \(p\) in the middle, \(eg\) 5 + 10, \(p\), 6 + 2
\(p\) > 7, \(p\) < 10 because 2 is the mode
Possible values of \(p\) are 8 and 9