Question
A four-sided die has three blue faces and one red face. The die is rolled.
Let B be the event a blue face lands down, and R be the event a red face lands down.
Write down
(i) P(B);
(ii) P(R).
If the blue face lands down, the die is not rolled again. If the red face lands down, the die is rolled once again. This is represented by the following tree diagram, where p, s, t are probabilities.
Find the value of p, of s and of t.
Guiseppi plays a game where he rolls the die. If a blue face lands down, he scores 2 and is finished. If the red face lands down, he scores 1 and rolls one more time. Let X be the total score obtained.
(i) Show that \({\text{P}}(X = 3) = \frac{3}{{16}}\) .
(ii) Find \({\text{P}}(X = 2)\) .
(i) Construct a probability distribution table for X.
(ii) Calculate the expected value of X.
If the total score is 3, Guiseppi wins \(\$ 10\). If the total score is 2, Guiseppi gets nothing.
Guiseppi plays the game twice. Find the probability that he wins exactly \(\$ 10\).
Answer/Explanation
Markscheme
(i) P(B) \( = \frac{3}{4}\) A1 N1
(ii) P(R) \( = \frac{1}{4}\) A1 N1
[2 marks]
\(p = \frac{3}{4}\) A1 N1
\(s = \frac{1}{4}\), \(t = \frac{3}{4}\) A1 N1
[2 marks]
(i) \({\text{P}}(X = 3)\)
\( = {\text{P (getting 1 and 2)}} = \frac{1}{4} \times \frac{3}{4}\) A1
\( = \frac{3}{{16}}\) AG N0
(ii) \({\text{P}}(X = 2) = \frac{1}{4} \times \frac{1}{4} + \frac{3}{4}{\text{ }}\left( {{\text{or }}1 – \frac{3}{{16}}} \right)\) (A1)
\( = \frac{{13}}{{16}}\) A1 N2
[3 marks]
(i)
A2 N2
(ii) evidence of using \({\text{E}}(X) = \sum{x{\text{P}}(X = x)} \) (M1)
\({\text{E}}(X) = 2\left( {\frac{{13}}{{16}}} \right) + 3\left( {\frac{3}{{16}}} \right)\) (A1)
\( = \frac{{35}}{{16}}{\text{ }}\left( { = 2\frac{3}{{16}}} \right)\) A1 N2
[5 marks]
win \(\$ 10 \Rightarrow \) scores 3 one time, 2 other time (M1)
\({\text{P}}(3) \times {\text{P}}(2) = \frac{{13}}{{16}} \times \frac{3}{{16}}\) (seen anywhere) A1
evidence of recognising there are different ways of winning \(\$ 10\) (M1)
e.g. \({\text{P}}(3) \times {\text{P}}(2) + {\text{P}}(2) \times {\text{P}}(3)\) , \(2\left( {\frac{{13}}{{16}} \times \frac{3}{{16}}} \right)\) , \(\frac{{36}}{{256}} + \frac{3}{{256}} + \frac{{36}}{{256}} + \frac{3}{{256}}\)
\({\text{P(win }}\$ 10) = \frac{{78}}{{256}}{\text{ }}\left( { = \frac{{39}}{{128}}} \right)\) A1 N3
[4 marks]
Question
The letters of the word PROBABILITY are written on 11 cards as shown below.
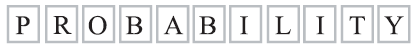
Two cards are drawn at random without replacement.
Let A be the event the first card drawn is the letter A.
Let B be the event the second card drawn is the letter B.
Find \({\rm{P}}(A)\) .
Find \({\rm{P}}(B|A)\) .
Find \({\rm{P}}(A \cap B)\) .
Answer/Explanation
Markscheme
\({\rm{P}}(A) = \frac{1}{{11}}\) A1 N1
[1 mark]
\({\rm{P}}(B|A) = \frac{2}{{10}}\) A2 N2
[2 marks]
recognising that \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B|A)\) (M1)
correct values (A1)
e.g. \({\rm{P}}(A \cap B) = \frac{1}{{11}} \times \frac{2}{{10}}\)
\({\rm{P}}(A \cap B) = \frac{2}{{110}}\) A1 N3
[3 marks]
Question
Two boxes contain numbered cards as shown below.
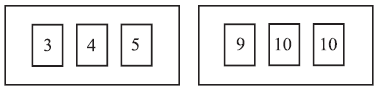
Two cards are drawn at random, one from each box.
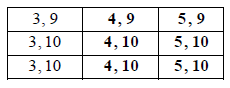
Copy and complete the table below to show all nine equally likely outcomes.
Let S be the sum of the numbers on the two cards.
Find the probability of each value of S.
Find the expected value of S.
Anna plays a game where she wins \(\$ 50\) if S is even and loses \(\$ 30\) if S is odd.
Anna plays the game 36 times. Find the amount she expects to have at the end of the 36 games.
Answer/Explanation
Markscheme
A2 N2
[2 marks]
\({\rm{P}}(12) = \frac{1}{9}\) , \({\rm{P}}(13) = \frac{3}{9}\) , \({\rm{P}}(14) = \frac{3}{9}\) , \({\rm{P}}(15) = \frac{2}{9}\) A2 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) A1
e.g. \({\rm{E}}(S) = 12 \times \frac{1}{9} + 13 \times \frac{3}{9} + 14 \times \frac{3}{9} + 15 \times \frac{2}{9}\)
\({\rm{E}}(S) = \frac{{123}}{9}\) A2 N2
[3 marks]
METHOD 1
correct expression for expected gain E(A) for 1 game (A1)
e.g. \(\frac{4}{9} \times 50 – \frac{5}{9} \times 30\)
\({\rm{E}}(A) = \frac{{50}}{9}\)
amount at end = expected gain for 1 game \( \times 36\) (M1)
= 200 (dollars) A1 N2
METHOD 2
attempt to find expected number of wins and losses (M1)
e.g. \(\frac{4}{9} \times 36\) , \(\frac{5}{9} \times 36\)
attempt to find expected gain E(G) (M1)
e.g. \(16 \times 50 – 30 \times 20\)
\({\text{E}}(G) = 200\) (dollars) A1 N2
[3 marks]
Question
In a class of 100 boys, 55 boys play football and 75 boys play rugby. Each boy must play at least one sport from football and rugby.
(i) Find the number of boys who play both sports.
(ii) Write down the number of boys who play only rugby.
One boy is selected at random.
(i) Find the probability that he plays only one sport.
(ii) Given that the boy selected plays only one sport, find the probability that he plays rugby.
Let A be the event that a boy plays football and B be the event that a boy plays rugby.
Explain why A and B are not mutually exclusive.
Show that A and B are not independent.
Answer/Explanation
Markscheme
(i) evidence of substituting into \(n(A \cup B) = n(A) + n(B) – n(A \cap B)\) (M1)
e.g. \(75 + 55 – 100\) , Venn diagram
30 A1 N2
(ii) 45 A1 N1
[3 marks]
(i) METHOD 1
evidence of using complement, Venn diagram (M1)
e.g. \(1 – p\) , \(100 – 30\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
METHOD 2
attempt to find P(only one sport) , Venn diagram (M1)
e.g. \(\frac{{25}}{{100}} + \frac{{45}}{{100}}\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
(ii) \(\frac{{45}}{{70}}\) \(\left( { = \frac{9}{{14}}} \right)\) A2 N2
[4 marks]
valid reason in words or symbols (R1)
e.g. \({\rm{P}}(A \cap B) = 0\) if mutually exclusive, \({\rm{P}}(A \cap B) \ne 0\) if not mutually exclusive
correct statement in words or symbols A1 N2
e.g. \({\rm{P}}(A \cap B) = 0.3\) , \({\rm{P}}(A \cup B) \ne {\rm{P}}(A) + {\rm{P}}(B)\) , \({\rm{P}}(A) + {\rm{P}}(B) > 1\) , some students play both sports, sets intersect
[2 marks]
valid reason for independence (R1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B)\) , \({\rm{P}}(B|A) = {\rm{P}}(B)\)
correct substitution A1A1 N3
e.g. \(\frac{{30}}{{100}} \ne \frac{{75}}{{100}} \times \frac{{55}}{{100}}\) , \(\frac{{30}}{{55}} \ne \frac{{75}}{{100}}\)
[3 marks]
Question
In a group of 16 students, 12 take art and 8 take music. One student takes neither art nor music. The Venn diagram below shows the events art and music. The values p , q , r and s represent numbers of students.
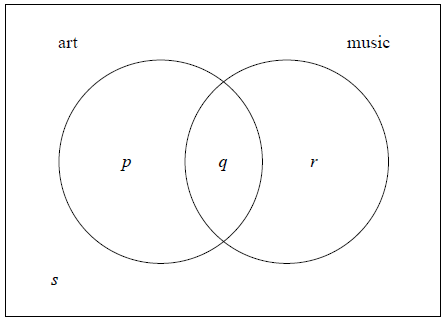
(i) Write down the value of s .
(ii) Find the value of q .
(iii) Write down the value of p and of r .
(i) A student is selected at random. Given that the student takes music, write down the probability the student takes art.
(ii) Hence, show that taking music and taking art are not independent events.
Two students are selected at random, one after the other. Find the probability that the first student takes only music and the second student takes only art.
Answer/Explanation
Markscheme
(i) \(s = 1\) A1 N1
(ii) evidence of appropriate approach (M1)
e.g. \(21 – 16\) , \(12 + 8 – q = 15\)
\(q = 5\) A1 N2
(iii) \(p = 7\) , \(r = 3\) A1A1 N2
[5 marks]
(i) \({\rm{P(art|music)}} = \frac{5}{8}\) A2 N2
(ii) METHOD 1
\({\rm{P(art)}} = \frac{{12}}{{16}}\) \(\left( { = \frac{3}{4}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{3}{4} \ne \frac{5}{8}\)
the events are not independent AG N0
METHOD 2
\({\rm{P(art)}} \times {\rm{P(music)}} = \frac{{96}}{{256}}\) \(\left( { = \frac{3}{8}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{{12}}{{16}} \times \frac{8}{{16}} \ne \frac{5}{{16}}\)
the events are not independent AG N0
[4 marks]
\({\text{P(first takes only music)}} = \frac{3}{{16}}\) (seen anywhere) A1
\({\text{P(second takes only art)}} = \frac{7}{{15}}\) (seen anywhere) A1
evidence of valid approach (M1)
e.g. \(\frac{3}{{16}} \times \frac{7}{{15}}\)
\({\text{P(music and art)}} = \frac{{21}}{{240}}\) \(\left( { = \frac{7}{{80}}} \right)\) A1 N2
[4 marks]
Question
A box contains six red marbles and two blue marbles. Anna selects a marble from the box. She replaces the marble and then selects a second marble.
Write down the probability that the first marble Anna selects is red.
Find the probability that Anna selects two red marbles.
Find the probability that one marble is red and one marble is blue.
Answer/Explanation
Markscheme
Note: In this question, method marks may be awarded for selecting without replacement, as noted in the examples.
\({\rm{P}}(R) = \frac{6}{8}\left( { = \frac{3}{4}} \right)\) A1 N1
[1 mark]
attempt to find \({\rm{P(Red)}} \times {\rm{P(Red)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}R{\rm{)}}\) , \(\frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\)
\({\rm{P}}(2R) = \frac{{36}}{{64}}\left( { = \frac{9}{{16}}} \right)\) A1 N2
[2 marks]
METHOD 1
attempt to find \({\rm{P(Red)}} \times {\rm{P(Blue)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}B{\rm{)}}\) , \(\frac{6}{8} \times \frac{2}{8}\) , \(\frac{6}{8} \times \frac{2}{7}\)
recognizing two ways to get one red, one blue (M1)
e.g. \({\rm{P}}(RB) + {\rm{P}}(BR)\) , \(2\left( {\frac{{12}}{{64}}} \right)\) , \(\frac{6}{8} \times \frac{2}{7} + \frac{2}{8} \times \frac{6}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
METHOD 2
recognizing that \({\rm{P}}(1R,1B)\) is \(1 – {\rm{P}}(2B) – {\rm{P}}(2R)\) (M1)
attempt to find \({\rm{P}}(2R)\) and \({\rm{P}}(2B)\) (M1)
e.g. \({\rm{P}}(2R) = \frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\) ; \({\rm{P}}(2B) = \frac{1}{4} \times \frac{1}{4}\) , \(\frac{2}{8} \times \frac{1}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
Question
Let \(f(x) = \frac{1}{2}{x^2} + kx + 8\) , where \(k \in \mathbb{Z}\) .
Find the values of k such that \(f(x) = 0\) has two equal roots.
Each value of k is equally likely for \( – 5 \le k \le 5\) . Find the probability that \(f(x) = 0\) has no roots.
Answer/Explanation
Markscheme
METHOD 1
evidence of discriminant (M1)
e.g. \({b^2} – 4ac\) , discriminant = 0
correct substitution into discriminant A1
e.g. \({k^2} – 4 \times \frac{1}{2} \times 8\) , \({k^2} – 16 = 0\)
\(k = \pm 4\) A1A1 N3
METHOD 2
recognizing that equal roots means perfect square (R1)
e.g. attempt to complete the square, \(\frac{1}{2}({x^2} + 2kx + 16)\)
correct working
e.g. \(\frac{1}{2}{(x + k)^2}\) , \(\frac{1}{2}{k^2} = 8\) A1
\(k = \pm 4\) A1A1 N3
[4 marks]
evidence of appropriate approach (M1)
e.g. \({b^2} – 4ac < 0\)
correct working for k A1
e.g. \( – 4 < k < 4\) , \({k^2} < 16\) , list all correct values of k
\(p = \frac{7}{{11}}\) A2 N3
[4 marks]
Question
Jar A contains three red marbles and five green marbles. Two marbles are drawn from the jar, one after the other, without replacement.
Jar B contains six red marbles and two green marbles. A fair six-sided die is tossed. If the score is \(1\) or \(2\), a marble is drawn from jar A. Otherwise, a marble is drawn from jar B.
Find the probability that
(i) none of the marbles are green;
(ii) exactly one marble is green.
Find the expected number of green marbles drawn from the jar.
(i) Write down the probability that the marble is drawn from jar B.
(ii) Given that the marble was drawn from jar B, write down the probability that it is red.
Given that the marble is red, find the probability that it was drawn from jar A.
Answer/Explanation
Markscheme
(i) attempt to find \({\rm{P(red)}} \times {\rm{P(red)}}\) (M1)
eg \(\frac{3}{8} \times \frac{2}{7}\) , \(\frac{3}{8} \times \frac{3}{8}\) , \(\frac{3}{8} \times \frac{2}{8}\)
\({\text{P(none green)}} = \frac{6}{{56}}\) \(\left( { = \frac{3}{{28}}} \right)\) A1 N2
(ii) attempt to find \({\rm{P(red)}} \times {\rm{P(green)}}\) (M1)
eg \(\frac{5}{8} \times \frac{3}{7}\) , \(\frac{3}{8} \times \frac{5}{8}\) , \(\frac{{15}}{{56}}\)
recognizing two ways to get one red, one green (M1)
eg \(2{\rm{P}}(R) \times {\rm{P}}(G)\) , \(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7}\) , \(\frac{3}{8} \times \frac{5}{8} \times 2\)
\({\text{P(exactly one green)}} = \frac{{30}}{{56}}\) \(\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[5 marks]
\({\text{P(both green)}} = \frac{{20}}{{56}}\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) A1
eg \(0 \times \frac{6}{{56}} + 1 \times \frac{{30}}{{56}} + 2 \times \frac{{20}}{{56}}\) , \(\frac{{30}}{{64}} + \frac{{50}}{{64}}\)
expected number of green marbles is \(\frac{{70}}{{56}}\) \(\left( { = \frac{5}{4}} \right)\) A1 N2
[3 marks]
(i) \({\text{P(jar B)}} = \frac{4}{6}\) \(\left( { = \frac{2}{3}} \right)\) A1 N1
(ii) \({\text{P(red| jar B)}} = \frac{6}{8}\) \(\left( { = \frac{3}{4}} \right)\) A1 N1
[2 marks]
recognizing conditional probability (M1)
eg \({\rm{P}}(A|R)\) , \(\frac{{{\text{P(jar A and red)}}}}{{{\rm{P(red)}}}}\) , tree diagram
attempt to multiply along either branch (may be seen on diagram) (M1)
eg \({\text{P(jar A and red)}} = \frac{1}{3} \times \frac{3}{8}\) \(\left( { = \frac{1}{8}} \right)\)
attempt to multiply along other branch (M1)
eg \({\text{P(jar B and red)}} = \frac{2}{3} \times \frac{6}{8}\) \(\left( { = \frac{1}{2}} \right)\)
adding the probabilities of two mutually exclusive paths (A1)
eg \({\rm{P(red)}} = \frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}\)
correct substitution
eg \({\text{P(jar A|red)}} = \frac{{\frac{1}{3} \times \frac{3}{8}}}{{\frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}}}\) , \(\frac{{\frac{1}{8}}}{{\frac{5}{8}}}\) A1
\({\text{P(jar A|red)}} = \frac{1}{5}\) A1 N3
[6 marks]
Question
A running club organizes a race to select girls to represent the club in a competition.
The times taken by the group of girls to complete the race are shown in the table below.
Find the value of \(p\) and of \(q\) .
A girl is chosen at random.
(i) Find the probability that the time she takes is less than \(14\) minutes.
(ii) Find the probability that the time she takes is at least \(26\) minutes.
A girl is selected for the competition if she takes less than \(x\) minutes to complete the race.
Given that \(40\%\) of the girls are not selected,
(i) find the number of girls who are not selected;
(ii) find \(x\) .
Girls who are not selected, but took less than \(25\) minutes to complete the race, are allowed another chance to be selected. The new times taken by these girls are shown in the cumulative frequency diagram below.
(i) Write down the number of girls who were allowed another chance.
(ii) Find the percentage of the whole group who were selected.
Answer/Explanation
Markscheme
attempt to find \(p\) (M1)
eg \(120 – 70\) , \(50 + 20 + x = 120\)
\(p = 50\) A1 N2
attempt to find \(q\) (M1)
eg \(180 – 20\) , \(200 – 20 – 20\)
\(q = 160\) A1 N2
[4 marks]
(i) \(\frac{{70}}{{200}}\) \(\left( { = \frac{7}{{20}}} \right)\) A1 N1
(ii) valid approach (M1)
eg \(20 + 20\) , \(200 – 160\)
\(\frac{{40}}{{200}}\) \(\left( { = \frac{1}{5}} \right)\) A1 N2
[3 marks]
(i) attempt to find number of girls (M1)
eg \(0.4\), \(\frac{{40}}{{100}} \times 200\)
\(80\) are not selected A1 N2
(ii) \(120\) are selected (A1)
\(x = 20\) A1 N2
[4 marks]
(i) \(30\) given second chance A1 N1
(ii) \(20\) took less than \(20\) minutes (A1)
attempt to find their selected total (may be seen in \(\%\) calculation) (M1)
eg \(120 + 20\) \(( = 140)\) , \(120 + \) their answer from (i)
\(70\) (\(\%\)) A1 N3
[4 marks]
Question
Ann and Bob play a game where they each have an eight-sided die. Ann’s die has three green faces and five red faces; Bob’s die has four green faces and four red faces. They take turns rolling their own die and note what colour faces up. The first player to roll green wins. Ann rolls first. Part of a tree diagram of the game is shown below.
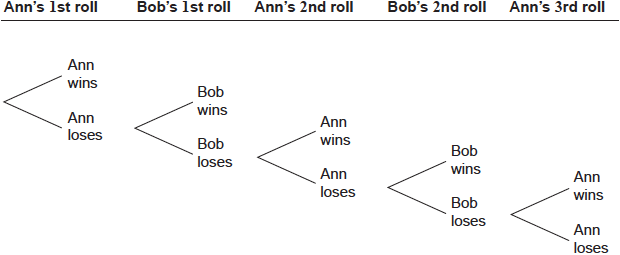
Find the probability that Ann wins on her first roll.
(i) The probability that Ann wins on her third roll is \(\frac{5}{8} \times \frac{4}{8} \times p \times q\ \times \frac{3}{8}\).
Write down the value of \(p\) and of \(q\).
(ii) The probability that Ann wins on her tenth roll is \(\frac{3}{8}{r^k}\) where \(r \in \mathbb{Q},{\text{ }}k \in \mathbb{Z}\).
Find the value of \(r\) and of \(k\).
Find the probability that Ann wins the game.
Answer/Explanation
Markscheme
recognizing Ann rolls green (M1)
eg\(\;\;\;{\text{P(G)}}\)
\(\frac{3}{8}\) A1 N2
[2 marks]
(i) \(p = \frac{4}{8},{\text{ }}q = \frac{5}{8}\) or \(q = \frac{4}{8},{\text{ }}p = \frac{5}{8}\) A1A1 N2
(ii) recognizes Ann and Bob lose \(9\) times (M1)
eg\(\;\;\;\(\overbrace {{A_L}{B_\(\overbrace {{A_L}{B_ \ldots \(\overbrace {{A_L}{B_{\text{ 9 times, }}\underbrace {\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right)}_{{\text{9 times}}}\)
\(k = 9\;\;\;\)(seen anywhere) A1 N2
correct working (A1)
eg\(\;\;\;{\left( {\frac{5}{8} \times \frac{4}{8}} \right)^9} \times \frac{3}{8},{\text{ }}\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \frac{3}{8}\)
\(r = \frac{{20}}{{64}}\;\;\;\left( { = \frac{5}{{16}}} \right)\) A1 N2
[6 marks]
recognize the probability is an infinite sum (M1)
eg\(\;\;\;\)Ann wins on her \({{\text{1}}^{{\text{st}}}}\) roll or \({{\text{2}}^{{\text{nd}}}}\) roll or \({{\text{3}}^{{\text{rd}}}}\) roll…, \({S_\infty }\)
recognizing GP (M1)
\({u_1} = \frac{3}{8}\;\;\;\)(seen anywhere) A1
\(r = \frac{{20}}{{64}}\;\;\;\)(seen anywhere) A1
correct substitution into infinite sum of GP A1
eg\(\;\;\;\frac{{\frac{3}{8}}}{{1 – \frac{5}{{16}}}},{\text{ }}\frac{3}{8}\left( {\frac{1}{{1 – \left( {\frac{5}{8} \times \frac{4}{8}} \right)}}} \right),{\text{ }}\frac{1}{{1 – \frac{5}{{16}}}}\)
correct working (A1)
eg\(\;\;\;\frac{{\frac{3}{8}}}{{\frac{{11}}{{16}}}},{\text{ }}\frac{3}{8} \times \frac{{16}}{{11}}\)
\({\text{P (Ann wins)}} = \frac{{48}}{{88}}\;\;\;\left( { = \frac{6}{{11}}} \right)\) A1 N1
[7 marks]
Total [15 marks]
Examiners report
Some teachers’ comments suggested that the word ‘loses’ in the diagram was misleading. But candidate scripts did not indicate any adverse effect.
a) Very well answered.
b) i) Probabilities \(p\) and \(q\) were typically found correctly. ii) Fewer candidates identified the common ratio and number of rolls correctly.
Few candidates recognized that this was an infinite geometric sum although some did see that a geometric progression was involved.
Some teachers’ comments suggested that the word ‘loses’ in the diagram was misleading, But candidate scripts did not indicate any adverse effect.
a) Very well answered.
b) i) Probabilities \(p\) and \(q\) were typically found correctly. ii) Fewer candidates identified the common ratio and number of rolls correctly.
Few candidates recognized that this was an infinite geometric sum although some did see that a geometric progression was involved.
Some teachers’ comments suggested that the word ‘loses’ in the diagram was misleading, But candidate scripts did not indicate any adverse effect.
a) Very well answered.
b) i) Probabilities \(p\) and \(q\) were typically found correctly. ii) Fewer candidates identified the common ratio and number of rolls correctly.
Few candidates recognized that this was an infinite geometric sum although some did see that a geometric progression was involved.
Question
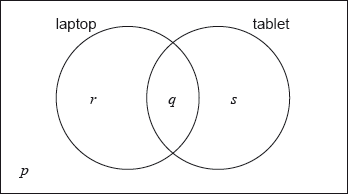
In a class of 21 students, 12 own a laptop, 10 own a tablet, and 3 own neither.
The following Venn diagram shows the events “own a laptop” and “own a tablet”.
The values \(p\), \(q\), \(r\) and \(s\) represent numbers of students.
A student is selected at random from the class.
Two students are randomly selected from the class. Let \(L\) be the event a “student owns a laptop”.
(i) Write down the value of \(p\).
(ii) Find the value of \(q\).
(iii) Write down the value of \(r\) and of \(s\).
(i) Write down the probability that this student owns a laptop.
(ii) Find the probability that this student owns a laptop or a tablet but not both.
(i) Copy and complete the following tree diagram. (Do not write on this page.)
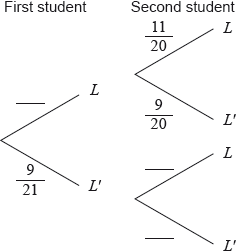
(ii) Write down the probability that the second student owns a laptop given that the first owns a laptop.
Answer/Explanation
Markscheme
(i) \(p = 3\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\((12 + 10 + 3) – 21,{\text{ }}22 – 18\)
\(q = 4\) A1 N2
(iii) \(r = 8,{\text{ }}s = 6\) A1A1 N2
(i) \(\frac{{12}}{{21}}{\text{ }}\left( { = \frac{4}{7}} \right)\) A2 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\(8 + 6,{\text{ }}r + s\)
\(\frac{{14}}{{21}}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1 N2
(i)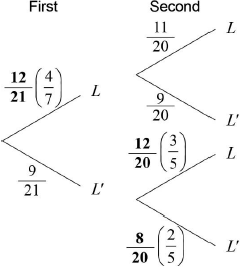 
A1A1A1 N3
(ii) \(\frac{{11}}{{20}}\) A1 N1
[4 marks]
Question
A bag contains 5 green balls and 3 white balls. Two balls are selected at random without replacement.
Complete the following tree diagram.
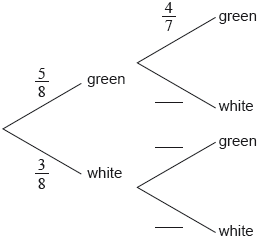
Find the probability that exactly one of the selected balls is green.
Markscheme
correct probabilities
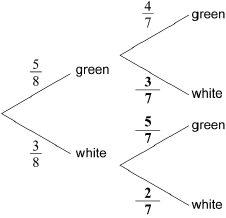A1A1A1 N3
Note: Award A1 for each correct bold answer.
[3 marks]
multiplying along branches (M1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7},{\text{ }}\frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}}\)
adding probabilities of correct mutually exclusive paths (A1)
eg\(\,\,\,\,\,\)\(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7},{\text{ }}\frac{{15}}{{56}} + \frac{{15}}{{56}}\)
\(\frac{{30}}{{56}}{\text{ }}\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[3 marks]
Examiners report
Question
Pablo drives to work. The probability that he leaves home before 07:00 is \(\frac{3}{4}\).
If he leaves home before 07:00 the probability he will be late for work is \(\frac{1}{8}\).
If he leaves home at 07:00 or later the probability he will be late for work is \(\frac{5}{8}\).
Copy and complete the following tree diagram.
Find the probability that Pablo leaves home before 07:00 and is late for work.
Find the probability that Pablo is late for work.
Given that Pablo is late for work, find the probability that he left home before 07:00.
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for each bold fraction.
[3 marks]
multiplying along correct branches (A1)
eg \(\frac{3}{4} \times \frac{1}{8}\)
P(leaves before 07:00 ∩ late) = \(\frac{3}{32}\) A1 N2
[2 marks]
multiplying along other “late” branch (M1)
eg \(\frac{1}{4} \times \frac{5}{8}\)
adding probabilities of two mutually exclusive late paths (A1)
eg \(\left( {\frac{3}{4} \times \frac{1}{8}} \right) + \left( {\frac{1}{4} \times \frac{5}{8}} \right),\,\,\frac{3}{{32}} + \frac{5}{{32}}\)
\({\text{P}}\left( L \right) = \frac{8}{{32}}\,\,\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
recognizing conditional probability (seen anywhere) (M1)
eg \({\text{P}}\left( {A|B} \right),\,\,{\text{P}}\left( {{\text{before 7}}|{\text{late}}} \right)\)
correct substitution of their values into formula (A1)
eg \(\frac{{\frac{3}{{32}}}}{{\frac{1}{4}}}\)
\({\text{P}}\left( {{\text{left before 07:00}}|{\text{late}}} \right) = \frac{3}{8}\) A1 N2
[3 marks]
valid approach (M1)
eg 1 − P(not late twice), P(late once) + P(late twice)
correct working (A1)
eg \(1 – \left( {\frac{3}{4} \times \frac{3}{4}} \right),\,\,2 \times \frac{1}{4} \times \frac{3}{4} + \frac{1}{4} \times \frac{1}{4}\)
\(\frac{7}{{16}}\) A1 N2
[3 marks]
Question
Two standard six-sided dice are tossed. A diagram representing the sample space is shown below.
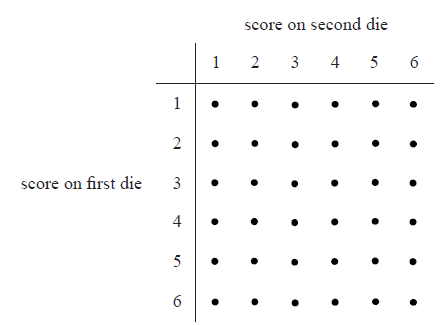
Let \(X\) be the sum of the scores on the two dice.
(i) Find \({\rm{P}}(X = 6)\) .
(ii) Find \({\rm{P}}(X > 6)\) .
(iii) Find \({\rm{P}}(X = 7|X > 6)\) .
Elena plays a game where she tosses two dice.
If the sum is 6, she wins 3 points.
If the sum is greater than 6, she wins 1 point.
If the sum is less than 6, she loses k points.
Find the value of k for which the game is fair.
Answer/Explanation
Markscheme
(i) number of ways of getting \(X = 6\) is 5 A1
\({\rm{P}}(X = 6) = \frac{5}{{36}}\) A1 N2
(ii) number of ways of getting \(X > 6\) is 21 A1
\({\rm{P}}(X > 6) = \frac{{21}}{{36}}\left( { = \frac{7}{{12}}} \right)\) A1 N2
(iii) \({\rm{P}}(X = 7|X > 6) = \frac{6}{{21}}\left( { = \frac{2}{7}} \right)\) A2 N2
[6 marks]
attempt to find \({\rm{P}}(X < 6)\) M1
e.g. \(1 – \frac{5}{{36}} – \frac{{21}}{{36}}\)
\({\rm{P}}(X < 6) = \frac{{10}}{{36}}\) A1
fair game if \({\rm{E}}(W) = 0\) (may be seen anywhere) R1
attempt to substitute into \({\rm{E}}(X)\) formula M1
e.g. \(3\left( {\frac{5}{{36}}} \right) + 1\left( {\frac{{21}}{{36}}} \right) – k\left( {\frac{{10}}{{36}}} \right)\)
correct substitution into \({\rm{E}}(W) = 0\) A1
e.g. \(3\left( {\frac{5}{{36}}} \right) + 1\left( {\frac{{21}}{{36}}} \right) – k\left( {\frac{{10}}{{36}}} \right) = 0\)
work towards solving M1
e.g. \(15 + 21 – 10k = 0\)
\(36 = 10k\) A1
\(k = \frac{{36}}{{10}}( = 3.6)\) A1 N4
[8 marks]