Question
In a class of 30 students, 19 play tennis, 3 play both tennis and volleyball, and 6 do not play either sport.
The following Venn diagram shows the events “plays tennis” and “plays volleyball”.
The values t and v represent numbers of students.
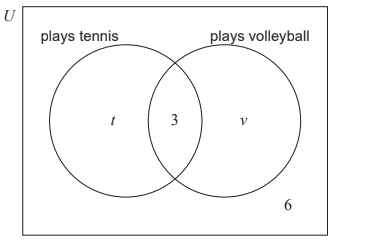
(i) Find the value of t .
(ii) Find the value of v . [4]
Find the probability that a randomly selected student from the class plays tennis or volleyball, but not both. [2]
Answer/Explanation
Ans:
(a)
(i)
valid approach to find t
eg t+ 3 = 19, 19 – 3
t =16 (may be seen on Venn diagram)
(ii)
valid approach to find v
eg t+ 3 + v + 6 = 30, 30- 19 – 6
v = 5 (may be seen on Venn diagram)
(b)
valid approach
eg 16+ 5 , 21 students, \(1-\frac{3+6}{30}\)
\(\frac{21}{30}(=\frac{7}{10})\)
Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
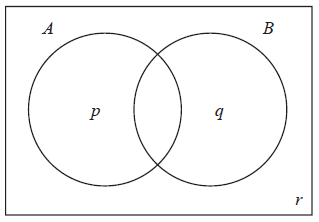
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B’)\) .
Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B’) = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]