Question
A four-sided die has three blue faces and one red face. The die is rolled.
Let B be the event a blue face lands down, and R be the event a red face lands down.
Write down
(i) P(B);
(ii) P(R).
If the blue face lands down, the die is not rolled again. If the red face lands down, the die is rolled once again. This is represented by the following tree diagram, where p, s, t are probabilities.
Find the value of p, of s and of t.
Guiseppi plays a game where he rolls the die. If a blue face lands down, he scores 2 and is finished. If the red face lands down, he scores 1 and rolls one more time. Let X be the total score obtained.
(i) Show that \({\text{P}}(X = 3) = \frac{3}{{16}}\) .
(ii) Find \({\text{P}}(X = 2)\) .
(i) Construct a probability distribution table for X.
(ii) Calculate the expected value of X.
If the total score is 3, Guiseppi wins \(\$ 10\). If the total score is 2, Guiseppi gets nothing.
Guiseppi plays the game twice. Find the probability that he wins exactly \(\$ 10\).
Answer/Explanation
Markscheme
(i) P(B) \( = \frac{3}{4}\) A1 N1
(ii) P(R) \( = \frac{1}{4}\) A1 N1
[2 marks]
\(p = \frac{3}{4}\) A1 N1
\(s = \frac{1}{4}\), \(t = \frac{3}{4}\) A1 N1
[2 marks]
(i) \({\text{P}}(X = 3)\)
\( = {\text{P (getting 1 and 2)}} = \frac{1}{4} \times \frac{3}{4}\) A1
\( = \frac{3}{{16}}\) AG N0
(ii) \({\text{P}}(X = 2) = \frac{1}{4} \times \frac{1}{4} + \frac{3}{4}{\text{ }}\left( {{\text{or }}1 – \frac{3}{{16}}} \right)\) (A1)
\( = \frac{{13}}{{16}}\) A1 N2
[3 marks]
(i)
A2 N2
(ii) evidence of using \({\text{E}}(X) = \sum{x{\text{P}}(X = x)} \) (M1)
\({\text{E}}(X) = 2\left( {\frac{{13}}{{16}}} \right) + 3\left( {\frac{3}{{16}}} \right)\) (A1)
\( = \frac{{35}}{{16}}{\text{ }}\left( { = 2\frac{3}{{16}}} \right)\) A1 N2
[5 marks]
win \(\$ 10 \Rightarrow \) scores 3 one time, 2 other time (M1)
\({\text{P}}(3) \times {\text{P}}(2) = \frac{{13}}{{16}} \times \frac{3}{{16}}\) (seen anywhere) A1
evidence of recognising there are different ways of winning \(\$ 10\) (M1)
e.g. \({\text{P}}(3) \times {\text{P}}(2) + {\text{P}}(2) \times {\text{P}}(3)\) , \(2\left( {\frac{{13}}{{16}} \times \frac{3}{{16}}} \right)\) , \(\frac{{36}}{{256}} + \frac{3}{{256}} + \frac{{36}}{{256}} + \frac{3}{{256}}\)
\({\text{P(win }}\$ 10) = \frac{{78}}{{256}}{\text{ }}\left( { = \frac{{39}}{{128}}} \right)\) A1 N3
[4 marks]
Question
There are 20 students in a classroom. Each student plays only one sport. The table below gives their sport and gender.
One student is selected at random.
(i) Calculate the probability that the student is a male or is a tennis player.
(ii) Given that the student selected is female, calculate the probability that the student does not play football.
Two students are selected at random. Calculate the probability that neither student plays football.
Answer/Explanation
Markscheme
(i) correct calculation (A1)
e.g. \(\frac{9}{{20}} + \frac{5}{{20}} – \frac{2}{{20}}\) , \(\frac{{4 + 2 + 3 + 3}}{{20}}\)
\({\text{P(male or tennis)}} = \frac{{12}}{{20}}\) A1 N2
(ii) correct calculation (A1)
e.g. \(\frac{6}{{20}} \div \frac{{11}}{{20}}\) , \(\frac{{3 + 3}}{{11}}\)
\({\text{P(not football|female)}} = \frac{6}{{11}}\) A1 N2
[4 marks]
\({\text{P(first not football)}} = \frac{{11}}{{20}}\) , \({\text{P(second not football)}} = \frac{{10}}{{19}}\) A1
\({\text{P(neither football)}} = \frac{{11}}{{20}} \times \frac{{10}}{{19}}\) A1
\({\text{P(neither football)}} = \frac{{110}}{{380}}\) A1 N1
[3 marks]
Question
Let A and B be independent events, where \({\text{P}}(A) = 0.6\) and \({\text{P}}(B) = x\) .
Write down an expression for \({\text{P}}(A \cap B)\) .
Given that \({\text{P}}(A \cup B) = 0.8\) ,
(i) find x ;
(ii) find \({\text{P}}(A \cap B)\) .
Hence, explain why A and B are not mutually exclusive.
Answer/Explanation
Markscheme
\({\text{P}}(A \cap B) = {\text{P}}(A) \times {\text{P}}(B)( = 0.6x)\) A1 N1
[1 mark]
(i) evidence of using \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
correct substitution A1
e.g. \(0.8 = 0.6 + x – 0.6x\) , \(0.2 = 0.4x\)
\(x = 0.5\) A1 N2
(ii) \({\text{P}}(A \cap B) = 0.3\) A1 N1
[4 marks]
valid reason, with reference to \({\text{P(}}A \cap B)\) R1 N1
e.g. \({\text{P(}}A \cap B) \ne 0\)
[1 mark]
Question
Consider the events A and B, where \({\rm{P}}(A) = 0.5\) , \({\rm{P}}(B) = 0.7\) and \({\rm{P}}(A \cap B) = 0.3\) .
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
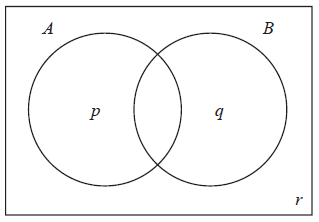
Write down the value of
(i) p ;
(ii) q ;
(iii) r.
Find the value of \({\rm{P}}(A|B’)\) .
Hence, or otherwise, show that the events A and B are not independent.
Answer/Explanation
Markscheme
(i) \(p = 0.2\) A1 N1
(ii) \(q = 0.4\) A1 N1
(iii) \(r = 0.1\) A1 N1
[3 marks]
\({\rm{P}}(A|B’) = \frac{2}{3}\) A2 N2
Note: Award A1 for an unfinished answer such as \(\frac{{0.2}}{{0.3}}\) .
[2 marks]
valid reason R1
e.g. \(\frac{2}{3} \ne 0.5\) , \(0.35 \ne 0.3\)
thus, A and B are not independent AG N0
[1 mark]
Question
José travels to school on a bus. On any day, the probability that José will miss the bus is \(\frac{1}{3}\) .
If he misses his bus, the probability that he will be late for school is \(\frac{7}{8}\) .
If he does not miss his bus, the probability that he will be late is \(\frac{3}{8}\) .
Let E be the event “he misses his bus” and F the event “he is late for school”.
The information above is shown on the following tree diagram.
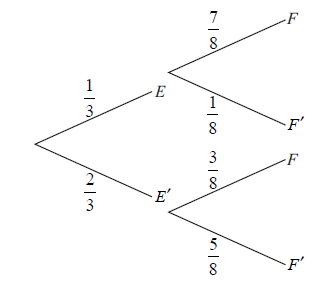
Find
(i) \({\rm{P}}(E \cap F)\) ;
(ii) \({\rm{P}}(F)\) .
Find the probability that
(i) José misses his bus and is not late for school;
(ii) José missed his bus, given that he is late for school.
The cost for each day that José catches the bus is 3 euros. José goes to school on Monday and Tuesday.
Copy and complete the probability distribution table.

The cost for each day that José catches the bus is 3 euros. José goes to school on Monday and Tuesday.
Find the expected cost for José for both days.
Answer/Explanation
Markscheme
(i) \(\frac{7}{{24}}\) A1 N1
(ii) evidence of multiplying along the branches (M1)
e.g. \(\frac{2}{3} \times \frac{5}{8}\) , \(\frac{1}{3} \times \frac{7}{8}\)
adding probabilities of two mutually exclusive paths (M1)
e.g. \(\left( {\frac{1}{3} \times \frac{7}{8}} \right) + \left( {\frac{2}{3} \times \frac{3}{8}} \right)\) , \(\left( {\frac{1}{3} \times \frac{1}{8}} \right) + \left( {\frac{2}{3} \times \frac{5}{8}} \right)\)
\({\rm{P}}(F) = \frac{{13}}{{24}}\) A1 N2
[4 marks]
(i) \(\frac{1}{3} \times \frac{1}{8}\) (A1)
\(\frac{1}{{24}}\) A1
(ii) recognizing this is \({\rm{P}}(E|F)\) (M1)
e.g. \(\frac{7}{{24}} \div \frac{{13}}{{24}}\)
\(\frac{{168}}{{312}}\) \(\left( { = \frac{7}{{13}}} \right)\) A2 N3
[5 marks]
 A2A1 N3
A2A1 N3
[3 marks]
correct substitution into \({\rm{E}}(X)\) formula (M1)
e.g. \(0 \times \frac{1}{9} + 3 \times \frac{4}{9} + 6 \times \frac{4}{9}\) , \(\frac{{12}}{9} + \frac{{24}}{9}\)
\({\rm{E}}(X) = 4\) (euros) A1 N2
[2 marks]
Question
The diagram below shows the probabilities for events A and B , with \({\rm{P}}(A’) = p\) .
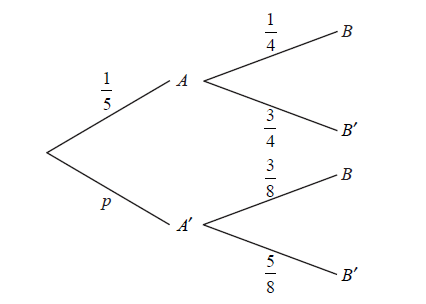
Write down the value of p .
Find \({\rm{P}}(B)\) .
Find \({\rm{P}}(A’|B)\) .
Answer/Explanation
Markscheme
\(p = \frac{4}{5}\) A1 N1
[1 mark]
multiplying along the branches (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4}\) , \(\frac{{12}}{{40}}\)
adding products of probabilities of two mutually exclusive paths (M1)
e.g. \(\frac{1}{5} \times \frac{1}{4} + \frac{4}{5} \times \frac{3}{8}\) , \(\frac{1}{{20}} + \frac{{12}}{{40}}\)
\({\rm{P}}(B) = \frac{{14}}{{40}}\) \(\left( { = \frac{7}{{20}}} \right)\) A1 N2
[3 marks]
appropriate approach which must include \({A’}\) (may be seen on diagram) (M1)
e.g. \(\frac{{{\rm{P}}(A’ \cap B)}}{{{\rm{P}}(B)}}\) (do not accept \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) )
\({\rm{P}}(A’|B) = \frac{{\frac{4}{5} \times \frac{3}{8}}}{{\frac{7}{{20}}}}\) (A1)
\({\rm{P}}(A’|B) = \frac{{12}}{{14}}\) \(\left( { = \frac{6}{7}} \right)\) A1 N2
[3 marks]
Question
In a group of 16 students, 12 take art and 8 take music. One student takes neither art nor music. The Venn diagram below shows the events art and music. The values p , q , r and s represent numbers of students.
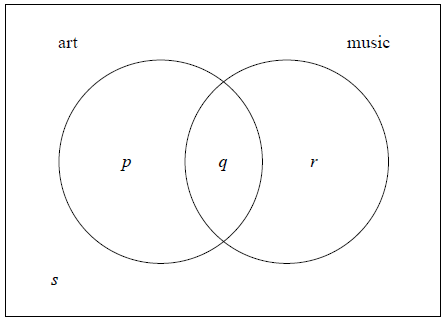
(i) Write down the value of s .
(ii) Find the value of q .
(iii) Write down the value of p and of r .
(i) A student is selected at random. Given that the student takes music, write down the probability the student takes art.
(ii) Hence, show that taking music and taking art are not independent events.
Two students are selected at random, one after the other. Find the probability that the first student takes only music and the second student takes only art.
Answer/Explanation
Markscheme
(i) \(s = 1\) A1 N1
(ii) evidence of appropriate approach (M1)
e.g. \(21 – 16\) , \(12 + 8 – q = 15\)
\(q = 5\) A1 N2
(iii) \(p = 7\) , \(r = 3\) A1A1 N2
[5 marks]
(i) \({\rm{P(art|music)}} = \frac{5}{8}\) A2 N2
(ii) METHOD 1
\({\rm{P(art)}} = \frac{{12}}{{16}}\) \(\left( { = \frac{3}{4}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{3}{4} \ne \frac{5}{8}\)
the events are not independent AG N0
METHOD 2
\({\rm{P(art)}} \times {\rm{P(music)}} = \frac{{96}}{{256}}\) \(\left( { = \frac{3}{8}} \right)\) A1
evidence of correct reasoning R1
e.g. \(\frac{{12}}{{16}} \times \frac{8}{{16}} \ne \frac{5}{{16}}\)
the events are not independent AG N0
[4 marks]
\({\text{P(first takes only music)}} = \frac{3}{{16}}\) (seen anywhere) A1
\({\text{P(second takes only art)}} = \frac{7}{{15}}\) (seen anywhere) A1
evidence of valid approach (M1)
e.g. \(\frac{3}{{16}} \times \frac{7}{{15}}\)
\({\text{P(music and art)}} = \frac{{21}}{{240}}\) \(\left( { = \frac{7}{{80}}} \right)\) A1 N2
[4 marks]
Question
A box contains six red marbles and two blue marbles. Anna selects a marble from the box. She replaces the marble and then selects a second marble.
Write down the probability that the first marble Anna selects is red.
Find the probability that Anna selects two red marbles.
Find the probability that one marble is red and one marble is blue.
Answer/Explanation
Markscheme
Note: In this question, method marks may be awarded for selecting without replacement, as noted in the examples.
\({\rm{P}}(R) = \frac{6}{8}\left( { = \frac{3}{4}} \right)\) A1 N1
[1 mark]
attempt to find \({\rm{P(Red)}} \times {\rm{P(Red)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}R{\rm{)}}\) , \(\frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\)
\({\rm{P}}(2R) = \frac{{36}}{{64}}\left( { = \frac{9}{{16}}} \right)\) A1 N2
[2 marks]
METHOD 1
attempt to find \({\rm{P(Red)}} \times {\rm{P(Blue)}}\) (M1)
e.g. \({\rm{P(}}R{\rm{)}} \times {\rm{P(}}B{\rm{)}}\) , \(\frac{6}{8} \times \frac{2}{8}\) , \(\frac{6}{8} \times \frac{2}{7}\)
recognizing two ways to get one red, one blue (M1)
e.g. \({\rm{P}}(RB) + {\rm{P}}(BR)\) , \(2\left( {\frac{{12}}{{64}}} \right)\) , \(\frac{6}{8} \times \frac{2}{7} + \frac{2}{8} \times \frac{6}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
METHOD 2
recognizing that \({\rm{P}}(1R,1B)\) is \(1 – {\rm{P}}(2B) – {\rm{P}}(2R)\) (M1)
attempt to find \({\rm{P}}(2R)\) and \({\rm{P}}(2B)\) (M1)
e.g. \({\rm{P}}(2R) = \frac{3}{4} \times \frac{3}{4}\) , \(\frac{6}{8} \times \frac{5}{7}\) ; \({\rm{P}}(2B) = \frac{1}{4} \times \frac{1}{4}\) , \(\frac{2}{8} \times \frac{1}{7}\)
\({\rm{P}}(1R,1B) = \frac{{24}}{{64}}\left( { = \frac{3}{8}} \right)\) A1 N2
[3 marks]
Question
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
(i) Copy and complete the following tree diagram.
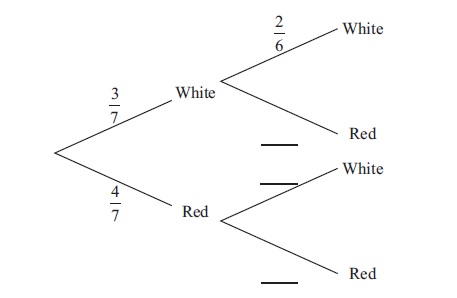
(ii) Find the probability that two white balls are chosen.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Find the probability that the two balls are white.
Bag A contains three white balls and four red balls. Two balls are chosen at random without replacement.
Bag B contains four white balls and three red balls. When two balls are chosen at random without replacement from bag B, the probability that they are both white is \(\frac{2}{7}\) .
A standard die is rolled. If 1 or 2 is obtained, two balls are chosen without replacement from bag A, otherwise they are chosen from bag B.
Given that both balls are white, find the probability that they were chosen from bag A.
Answer/Explanation
Markscheme
(i)
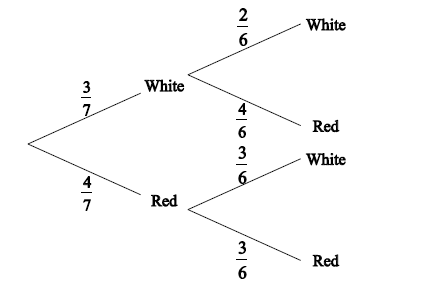
\(\frac{4}{6},\frac{3}{6}{\rm{and}}\frac{3}{6}\left( {\frac{2}{3},\frac{1}{2}{\rm{and}}\frac{1}{2}} \right)\) A1A1A1 N3
(ii) multiplying along the correct branches (may be seen on diagram) (A1)
e.g. \(\frac{3}{7} \times \frac{2}{6}\)
\(\frac{6}{{42}}\left( { = \frac{1}{7}} \right)\) A1 N2
[5 marks]
\({\rm{P(bag A) = }}\frac{2}{6}\left( { = \frac{1}{3}} \right)\) , \({\rm{P(bag B) = }}\frac{4}{6}\left( { = \frac{2}{3}} \right)\) (seen anywhere) (A1)(A1)
appropriate approach (M1)
e.g. \({\rm{P(}}WW \cap A) + {\rm{P}}(WW \cap B)\)
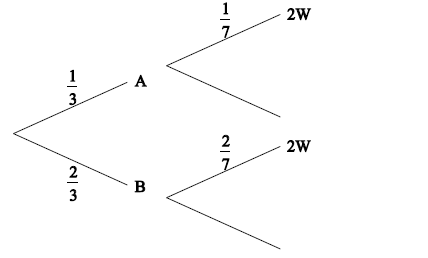
correct calculation A1
e.g. \(\frac{1}{3} \times \frac{1}{7} + \frac{2}{3} \times \frac{2}{7}\) , \(\frac{2}{{42}} + \frac{8}{{42}}\)
\({\rm{P}}(2W) = \frac{{60}}{{252}}\left( { = \frac{5}{{21}}} \right)\) A1 N3
[5 marks]
recognizing conditional probability (M1)
e.g. \(\frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}}\) , \({\rm{P}}(A|WW) = \frac{{{\rm{P}}(WW \cap A)}}{{{\rm{P}}(WW)}}\)
correct numerator (A1)
e.g. \({\rm{P}}(A \cap WW) = \frac{6}{{42}} \times \frac{2}{6},\frac{1}{{21}}\)
correct denominator (A1)
e.g. \(\frac{6}{{252}},\frac{5}{{21}}\)
probability \(\frac{{84}}{{420}}\left( { = \frac{1}{5}} \right)\) A1 N3
[4 marks]
Question
Celeste wishes to hire a taxicab from a company which has a large number of taxicabs.
The taxicabs are randomly assigned by the company.
The probability that a taxicab is yellow is 0.4.
The probability that a taxicab is a Fiat is 0.3.
The probability that a taxicab is yellow or a Fiat is 0.6.
Find the probability that the taxicab hired by Celeste is not a yellow Fiat.
Answer/Explanation
Markscheme
recognize need for intersection of Y and F (R1)
eg \({\text{P}}(Y \cap F){\text{, }}0.3 \times 0.4\)
valid approach to find \({\text{P}}(Y \cap F)\) (M1)
eg \({\text{P}}(Y) + {\text{P}}(F) – {\text{P}}(Y \cup F)\), Venn diagram
correct working (may be seen in Venn diagram) (A1)
eg \(0.4 + 0.3 – 0.6\)
\({\text{P}}(Y \cap F) = 0.1\) A1
recognize need for complement of \(Y \cap F\) (M1)
eg \(1 – {\text{P}}(Y \cap F){\text{, }}1 – 0.1\)
\({\text{P}}\left( {(Y \cap F)’} \right) = 0.9\) A1 N3
[6 marks]
Examiners report
Question
Adam travels to school by car (\(C\)) or by bicycle (\(B\)). On any particular day he is equally likely to travel by car or by bicycle.
The probability of being late (\(L\)) for school is \(\frac{1}{6}\) if he travels by car.
The probability of being late for school is \(\frac{1}{3}\) if he travels by bicycle.
This information is represented by the following tree diagram.
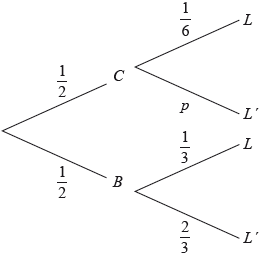
Find the value of \(p\).
Find the probability that Adam will travel by car and be late for school.
Find the probability that Adam will be late for school.
Given that Adam is late for school, find the probability that he travelled by car.
Adam will go to school three times next week.
Find the probability that Adam will be late exactly once.
Answer/Explanation
Markscheme
correct working (A1)
eg\(\;\;\;1 – \frac{1}{6}\)
\(p = \frac{5}{6}\) A1 N2
[2 marks]
multiplying along correct branches (A1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6}\)
\({\text{P}}(C \cap L) = \frac{1}{{12}}\) A1 N2
[2 marks]
multiplying along the other branch (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{3}\)
adding probabilities of their \(2\) mutually exclusive paths (M1)
eg\(\;\;\;\frac{1}{2} \times \frac{1}{6} + \frac{1}{2} \times \frac{1}{3}\)
correct working (A1)
eg\(\;\;\;\frac{1}{{12}} + \frac{1}{6}\)
\({\text{P}}(L) = \frac{3}{{12}}\;\;\;\left( { = \frac{1}{4}} \right)\) A1 N3
[4 marks]
recognizing conditional probability (seen anywhere) (M1)
eg\(\;\;\;{\text{P}}(C|L)\)
correct substitution of their values into formula (A1)
eg\(\frac{{\frac{1}{{12}}}}{{\frac{3}{{12}}}}\)
\({\text{P}}(C|L) = \frac{1}{3}\) A1 N2
[3 marks]
valid approach (M1)
eg \(X \sim B\) \(\left({3,{\text{ }}\frac{1}{4}} \right),{\text{ }}\left({\frac{1}{4}} \right){\left({\frac{3}{4}} \right)^2},{\text{ }}\left( {\begin{array}{*{20}{c}}3 \\1\end{array}} \right)\), three ways it could happen
correct substitution (A1)
eg \(\;\;\;\left({\begin{array}{*{20}{c}}3\\1\end{array}}\right){\left({\frac{1}{4}}\right)^1}{\left({\frac{3}{4}} \right)^2},{\text{ }}\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4} + \frac{3}{4} \times\frac{1}{4}\times\frac{3}{4} + \frac{3}{4}\times\frac{3}{4}\times\frac{1}{4}\)
correct working (A1)
eg\(\;\;\;3\left( {\frac{1}{4}} \right)\left( {\frac{9}{{16}}} \right),{\text{ }}\frac{9}{{64}} + \frac{9}{{64}} + \frac{9}{{64}}\)
\(\frac{{27}}{{64}}\) A1 N2
[4 marks]
Total [15 marks]
Question
Ann and Bob play a game where they each have an eight-sided die. Ann’s die has three green faces and five red faces; Bob’s die has four green faces and four red faces. They take turns rolling their own die and note what colour faces up. The first player to roll green wins. Ann rolls first. Part of a tree diagram of the game is shown below.
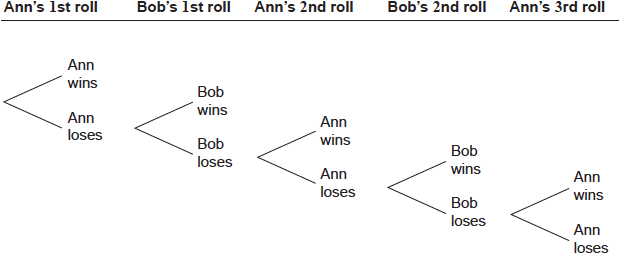
Find the probability that Ann wins on her first roll.
(i) The probability that Ann wins on her third roll is \(\frac{5}{8} \times \frac{4}{8} \times p \times q\ \times \frac{3}{8}\).
Write down the value of \(p\) and of \(q\).
(ii) The probability that Ann wins on her tenth roll is \(\frac{3}{8}{r^k}\) where \(r \in \mathbb{Q},{\text{ }}k \in \mathbb{Z}\).
Find the value of \(r\) and of \(k\).
Find the probability that Ann wins the game.
Answer/Explanation
Markscheme
recognizing Ann rolls green (M1)
eg\(\;\;\;{\text{P(G)}}\)
\(\frac{3}{8}\) A1 N2
[2 marks]
(i) \(p = \frac{4}{8},{\text{ }}q = \frac{5}{8}\) or \(q = \frac{4}{8},{\text{ }}p = \frac{5}{8}\) A1A1 N2
(ii) recognizes Ann and Bob lose \(9\) times (M1)
eg\(\;\;\;\(\overbrace {{A_L}{B_\(\overbrace {{A_L}{B_ \ldots \(\overbrace {{A_L}{B_{\text{ 9 times, }}\underbrace {\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right)}_{{\text{9 times}}}\)
\(k = 9\;\;\;\)(seen anywhere) A1 N2
correct working (A1)
eg\(\;\;\;{\left( {\frac{5}{8} \times \frac{4}{8}} \right)^9} \times \frac{3}{8},{\text{ }}\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \frac{3}{8}\)
\(r = \frac{{20}}{{64}}\;\;\;\left( { = \frac{5}{{16}}} \right)\) A1 N2
[6 marks]
recognize the probability is an infinite sum (M1)
eg\(\;\;\;\)Ann wins on her \({{\text{1}}^{{\text{st}}}}\) roll or \({{\text{2}}^{{\text{nd}}}}\) roll or \({{\text{3}}^{{\text{rd}}}}\) roll…, \({S_\infty }\)
recognizing GP (M1)
\({u_1} = \frac{3}{8}\;\;\;\)(seen anywhere) A1
\(r = \frac{{20}}{{64}}\;\;\;\)(seen anywhere) A1
correct substitution into infinite sum of GP A1
eg\(\;\;\;\frac{{\frac{3}{8}}}{{1 – \frac{5}{{16}}}},{\text{ }}\frac{3}{8}\left( {\frac{1}{{1 – \left( {\frac{5}{8} \times \frac{4}{8}} \right)}}} \right),{\text{ }}\frac{1}{{1 – \frac{5}{{16}}}}\)
correct working (A1)
eg\(\;\;\;\frac{{\frac{3}{8}}}{{\frac{{11}}{{16}}}},{\text{ }}\frac{3}{8} \times \frac{{16}}{{11}}\)
\({\text{P (Ann wins)}} = \frac{{48}}{{88}}\;\;\;\left( { = \frac{6}{{11}}} \right)\) A1 N1
[7 marks]
Total [15 marks]
Question
In a group of 20 girls, 13 take history and 8 take economics. Three girls take both history and economics, as shown in the following Venn diagram. The values \(p\) and \(q\) represent numbers of girls.
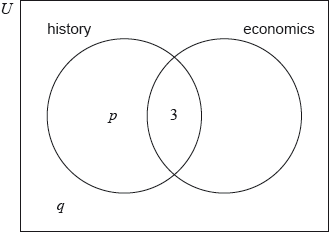
Find the value of \(p\);
Find the value of \(q\).
A girl is selected at random. Find the probability that she takes economics but not history.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 = 13,{\text{ }}13 – 3\)
\(p = 10\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(p + 3 + 5 + q = 20,{\text{ }}10 – 10 – 8\)
\(q = 2\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(20 – p – q – 3,{\text{ }}1 – \frac{{15}}{{20}},{\text{ }}n(E \cap H’) = 5\)
\(\frac{5}{{20}}\,\,\,\left( {\frac{1}{4}} \right)\) A1 N2
[2 marks]
Question
Pablo drives to work. The probability that he leaves home before 07:00 is \(\frac{3}{4}\).
If he leaves home before 07:00 the probability he will be late for work is \(\frac{1}{8}\).
If he leaves home at 07:00 or later the probability he will be late for work is \(\frac{5}{8}\).
Copy and complete the following tree diagram.
Find the probability that Pablo leaves home before 07:00 and is late for work.
Find the probability that Pablo is late for work.
Given that Pablo is late for work, find the probability that he left home before 07:00.
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for each bold fraction.
[3 marks]
multiplying along correct branches (A1)
eg \(\frac{3}{4} \times \frac{1}{8}\)
P(leaves before 07:00 ∩ late) = \(\frac{3}{32}\) A1 N2
[2 marks]
multiplying along other “late” branch (M1)
eg \(\frac{1}{4} \times \frac{5}{8}\)
adding probabilities of two mutually exclusive late paths (A1)
eg \(\left( {\frac{3}{4} \times \frac{1}{8}} \right) + \left( {\frac{1}{4} \times \frac{5}{8}} \right),\,\,\frac{3}{{32}} + \frac{5}{{32}}\)
\({\text{P}}\left( L \right) = \frac{8}{{32}}\,\,\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
recognizing conditional probability (seen anywhere) (M1)
eg \({\text{P}}\left( {A|B} \right),\,\,{\text{P}}\left( {{\text{before 7}}|{\text{late}}} \right)\)
correct substitution of their values into formula (A1)
eg \(\frac{{\frac{3}{{32}}}}{{\frac{1}{4}}}\)
\({\text{P}}\left( {{\text{left before 07:00}}|{\text{late}}} \right) = \frac{3}{8}\) A1 N2
[3 marks]
valid approach (M1)
eg 1 − P(not late twice), P(late once) + P(late twice)
correct working (A1)
eg \(1 – \left( {\frac{3}{4} \times \frac{3}{4}} \right),\,\,2 \times \frac{1}{4} \times \frac{3}{4} + \frac{1}{4} \times \frac{1}{4}\)
\(\frac{7}{{16}}\) A1 N2
[3 marks]
