Question
Jar A contains three red marbles and five green marbles. Two marbles are drawn from the jar, one after the other, without replacement.
Jar B contains six red marbles and two green marbles. A fair six-sided die is tossed. If the score is \(1\) or \(2\), a marble is drawn from jar A. Otherwise, a marble is drawn from jar B.
Find the probability that
(i) none of the marbles are green;
(ii) exactly one marble is green.
Find the expected number of green marbles drawn from the jar.
(i) Write down the probability that the marble is drawn from jar B.
(ii) Given that the marble was drawn from jar B, write down the probability that it is red.
Given that the marble is red, find the probability that it was drawn from jar A.
Answer/Explanation
Markscheme
(i) attempt to find \({\rm{P(red)}} \times {\rm{P(red)}}\) (M1)
eg \(\frac{3}{8} \times \frac{2}{7}\) , \(\frac{3}{8} \times \frac{3}{8}\) , \(\frac{3}{8} \times \frac{2}{8}\)
\({\text{P(none green)}} = \frac{6}{{56}}\) \(\left( { = \frac{3}{{28}}} \right)\) A1 N2
(ii) attempt to find \({\rm{P(red)}} \times {\rm{P(green)}}\) (M1)
eg \(\frac{5}{8} \times \frac{3}{7}\) , \(\frac{3}{8} \times \frac{5}{8}\) , \(\frac{{15}}{{56}}\)
recognizing two ways to get one red, one green (M1)
eg \(2{\rm{P}}(R) \times {\rm{P}}(G)\) , \(\frac{5}{8} \times \frac{3}{7} + \frac{3}{8} \times \frac{5}{7}\) , \(\frac{3}{8} \times \frac{5}{8} \times 2\)
\({\text{P(exactly one green)}} = \frac{{30}}{{56}}\) \(\left( { = \frac{{15}}{{28}}} \right)\) A1 N2
[5 marks]
\({\text{P(both green)}} = \frac{{20}}{{56}}\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) A1
eg \(0 \times \frac{6}{{56}} + 1 \times \frac{{30}}{{56}} + 2 \times \frac{{20}}{{56}}\) , \(\frac{{30}}{{64}} + \frac{{50}}{{64}}\)
expected number of green marbles is \(\frac{{70}}{{56}}\) \(\left( { = \frac{5}{4}} \right)\) A1 N2
[3 marks]
(i) \({\text{P(jar B)}} = \frac{4}{6}\) \(\left( { = \frac{2}{3}} \right)\) A1 N1
(ii) \({\text{P(red| jar B)}} = \frac{6}{8}\) \(\left( { = \frac{3}{4}} \right)\) A1 N1
[2 marks]
recognizing conditional probability (M1)
eg \({\rm{P}}(A|R)\) , \(\frac{{{\text{P(jar A and red)}}}}{{{\rm{P(red)}}}}\) , tree diagram
attempt to multiply along either branch (may be seen on diagram) (M1)
eg \({\text{P(jar A and red)}} = \frac{1}{3} \times \frac{3}{8}\) \(\left( { = \frac{1}{8}} \right)\)
attempt to multiply along other branch (M1)
eg \({\text{P(jar B and red)}} = \frac{2}{3} \times \frac{6}{8}\) \(\left( { = \frac{1}{2}} \right)\)
adding the probabilities of two mutually exclusive paths (A1)
eg \({\rm{P(red)}} = \frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}\)
correct substitution
eg \({\text{P(jar A|red)}} = \frac{{\frac{1}{3} \times \frac{3}{8}}}{{\frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{6}{8}}}\) , \(\frac{{\frac{1}{8}}}{{\frac{5}{8}}}\) A1
\({\text{P(jar A|red)}} = \frac{1}{5}\) A1 N3
[6 marks]
Question
The following diagram shows a board which is divided into three regions \(A\), \(B\) and \(C\).
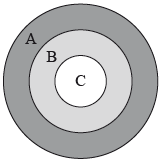
A game consists of a contestant throwing one dart at the board. The probability of hitting each region is given in the following table.
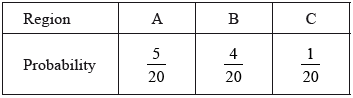
Find the probability that the dart does not hit the board.
The contestant scores points as shown in the following table.

Given that the game is fair, find the value of \(q\).
Answer/Explanation
Markscheme
evidence of summing probabilities to \(1\) (M1)
eg\(\;\;\;\frac{5}{{20}} + \frac{4}{{20}} + \frac{1}{{20}} + p = 1,\;\;\;\sum { = 1} \)
correct working (A1)
eg\(\;\;\;p = 1 – \frac{{10}}{{20}}\)
\(p = \frac{{10}}{{20}}\;\;\;\left( { = \frac{1}{2}} \right)\) A1 N2
[3 marks]
correct substitution into \({\text{E}}(X)\) (A1)
eg\(\;\;\;\frac{4}{{20}}(q) + \frac{1}{{20}}(10) + \frac{{10}}{{20}}( – 3)\)
valid reasoning for fair game (seen anywhere, including equation) (M1)
eg\(\;\;\;{\text{E}}(X) = 0\), points lost\( = \)points gained
correct working (A1)
eg\(\;\;\;4q + 10 – 30 = 0,\;\;\;\frac{4}{{20}}q + \frac{{10}}{{20}} = \frac{{30}}{{20}}\)
\(q = 5\) A1 N2
[4 marks]
Total [7 marks]