Question
[with GDC]
The random variable \(X\) is normally distributed with \(μ = 100\) and \(σ = 20\), i.e. \(N(100,20^{2})\).
(a) Find the probabilities
(i) \(P(X < 90)\) (ii) \(P(90 < X < 130)\) (iii) \(P(X > 130)\)
(b) Sketch a diagram to represent the information in question (a).
(c) Write down the standardised values of \(90, 100\) and \(130\).
(d) Sketch a diagram, similar that of (b), containing the standardised values above.
Answer/Explanation
Ans
(a) \(P(X < 90) = 0.308\) \(P(90 < X < 130) = 0.625\) \(P(X > 130) = 0.067\)
(b) 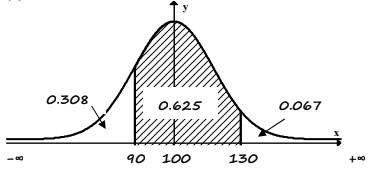
(c) The standardised values are \(-0.5, 0\) and \(1.5\) respectively
(d) 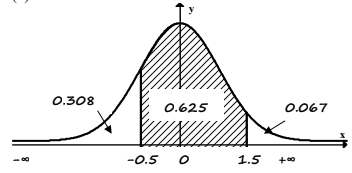
Question
[with GDC]
The random variable \(X\) follows a normal distribution with \(μ = 100\) and \(σ = 20\).
(a) Given that \(P(X < a) = 0.8\) find the value of \(a\).
(b) Given that \(P(X > b) = 0.3\) find the value of \(b\).
(c) Find \(Q_{1}\) and \(Q_{3}\).
Answer/Explanation
Ans
(a) (use tail left, area \(0.8\)) a = \(116.8\)
(b) (use tail right, area \(0.3\)) b=\(110.5\)
(c) (use tail central, area \(0.5\)) \(Q_{1}=86.5\) and \(Q_{3}=113.5\)
Question
[without GDC]
The random variable \(X\) is normally distributed with \(μ = 100\). It given that \(P(X > 130) = 0.2\)
Write down the values of the following probabilities
(a) \(P(X < 130)\)
(b) \(P(X < 70)\)
(c) \(P(100<X < 130)\)
(d) \(P(70<X < 130)\)
Answer/Explanation
Ans
(a) \(P(X < 130)\) = \(0.8\)
(b) \(P(X < 70) = 0.2\)
(c) \(P(100<X < 130) = 0.3\)
(d) \(P(70<X < 130) = 0.6\)
Question
[with GDC]
The random variable \(X\) follows a normal distribution with mean \(μ\) unknown and \(σ = 20\).
Given that \(P(X < 130) = 0.8\) find the value of \(μ\).
Answer/Explanation
Ans
\(\frac{X-\mu }{\sigma }=z\Leftrightarrow \frac{130-\mu }{20}=0.842\)
\(\Leftrightarrow \mu =113.2\)
Question
[with GDC]
The random variable \(X\) follows a normal distribution with mean \(μ = 100\) and \(σ\) unknown.
Given that \(P(X < 130) = 0.8\) find the value of \(σ\).
Answer/Explanation
Ans
\(\frac{X-\mu }{\sigma }=z\Leftrightarrow \frac{130-100}{\sigma }=0.842\)
\(\Leftrightarrow \sigma =35.6\)
Question
[with GDC]
For the normally distributed random variable \(X, P(X < 60) = 0.2\) and \(P(X > 130) = 0.1\).
Find the values of \(μ\) and of \(σ\).
Answer/Explanation
Ans
We use \(\frac{X-\mu }{\sigma }\)= \(z\) twice.
\(\frac{60-\mu }{\sigma }=-0.84162\Leftrightarrow 60-\mu =-0.84162\sigma \Leftrightarrow \mu -0.84162\sigma =60\)
\(\frac{130-\mu }{\sigma }=1.28155 \Leftrightarrow 130-\mu =1.28155\sigma \Leftrightarrow \mu +1.28155\sigma =130\)
System gives \(\mu =87.7\) and \(\sigma =33.0\)
Question
[with GDC]
The weight \(X\) of a particular animal is normally distributed with \(μ = 200\) kg and \(σ = 15\)kg.
An animal of this population is overweight if it has weight greater than \(230\) kg
(a) Find the probability than an animal is overweight.
(b) We select \(2\) animals of this population. Find the probabilities that
(i) both animals are overweight (ii) only one animal is overweight.
(c) We select \(7\) animals of this population. Find the probability that exactly two of them are overweight.
Answer/Explanation
Ans
(a) \(P(X > 230)= 0.02275\)
(b) (i) \((0.02275)^{2}=0.000518\) (ii) \((0.02275)\times (1-0.02275)\times 2=0.0445\)
(c) \(Y\) follows \(B (n , p )\) with \(n = 7, p = 0.02275\)
\(P (Y= 2) 0.00969\)
Question
[with GDC]
The mass of packets of a breakfast cereal is normally distributed with a mean of \(750\) g and standard deviation of \(25\) g.
(a) Find the probability that a packet chosen at random has mass
(i) less than \(740\) g; (ii) at least \(780\) g; (iii) between \(740\) g and 780\) g.
(b) Two packets are chosen at random. What is the probability that both packets have a mass which is less than \(740\) g?
(c) The mass of \(70\)% of the packets is more than \(x\) grams. Find the value of \(x\).
Answer/Explanation
Ans
(a) \(M\sim N(750,625)\)
(i) \(P (M < 740 g) = 0.345\)
(ii) \(P (M > 780 g) = 0.115\)
(iii) \(P(740 < M < 780) = 0.540\)
(b) P (both < \(740\)) = \(0.345^{2}=0.119\)
(c) x = \(737\) g
Question
[with GDC]
The heights, \(H\), of the people in a certain town are normally distributed with mean \(170\) cm and standard deviation \(20\) cm.
(a) A person is selected at random. Find the probability that his height is less than \(185\) cm.
(b) Given that \(P(H >d) = 0.6808\), find the value of \(d\).
Answer/Explanation
Ans
(a) \(0.773\)
(b) \(d = 161\)
Question
[with GDC]
The heights of a group of students are normally distributed with a mean of \(160\) cm and a standard deviation of 20 cm.
(a) A student is chosen at random. Find the probability that the student’s height is greater than \(180\) cm.
(b) In this group of students, \(11.9\)% have heights less than \(d\) cm. Find the value of \(d\).
Answer/Explanation
Ans
(a) \(0.159\)
(b) \(d = 136\)
Question
[with GDC]
The weights of a group of children are normally distributed with a mean of \(22.5\) kg and a standard deviation of \(2.2\) kg.
(a) Write down the probability that a child selected at random has a weight more than \(25.8\) kg.
(b) Of the group \(95\)% weigh less than \(k\) kilograms. Find the value of \(k\).
(c) The diagram below shows a normal curve. On the diagram, shade the region that represents the following information:
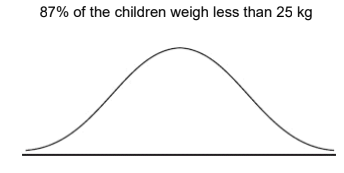
Answer/Explanation
Ans
(a) \(0.0668\)
(b) \(k = 26.1\) kg
(c) 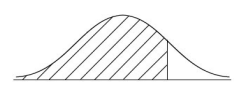
Question
[with GDC]
Intelligence Quotient (IQ) in a certain population is normally distributed with a mean of \(100\) and a standard deviation of \(15\).
(a) What percentage of the population has an IQ between \(90\) and \(125\)?
(b) If two persons are chosen at random from the population, what is the probability that both have an IQ greater than \(125\)?
Answer/Explanation
Ans
(a) P\((90 < X < 125) = 0.701\)
\(70.1\) percent of the population (accept \(70\) percent).
(b) \(P(X\geq 125)=0.0478\)
P(both persons having \(IQ\geq 125) = (0.0478)^{2}=0.00228\)
Question
[with GDC]
The heights of certain plants are normally distributed. The plants are classified into three categories.
The shortest \(12.92\)% are in category A.
The tallest \(10.38\)% are in category C.
All the other plants are in category B with heights between \(r\) cm and \(t\) cm.
(a) Complete the following diagram to represent this information.
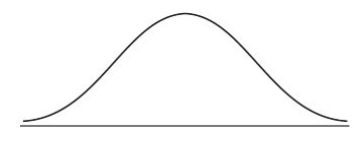
(b) Given that the mean height is \(6.84\) cm and the standard deviation \(0.25\) cm, find the value of \(r\) and of \(t\).
Answer/Explanation
Ans
(a) 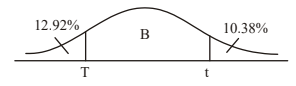
(b) \(r = 6.56\) \(t = 7.16\)
Question
[with GDC]
It is claimed that the masses of a population of lions are normally distributed with a mean mass of \(310\) kg and a standard deviation of \(30\) kg.
(a) Calculate the probability that a lion selected at random will have a mass of \(350\) kg or more.
(b) The probability that the mass of a lion lies between \(a\) and \(b\) is \(0.95\), where \(a\) and \(b\) are symmetric about the mean. Find the value of \(a\) and of \(b\).
Answer/Explanation
Ans
(a) \(P(M \geq 350) = 0.0912\)
(b) 
either tail left, tail right for each endpoint or directly tail central with Area = \(0.95\)
\(251 < M < 369\)
Question
[with GDC]
Residents of a small town have savings which are normally distributed with a mean of \($ 3000\) and a standard deviation of \($500\).
(a) What percentage of townspeople have savings greater than \($ 3200\)?
(b) Two townspeople are chosen at random. What is the probability that both of them have savings between \($ 2300\) and \($ 3300\)?
(c) The percentage of townspeople with savings less than d dollars is \(74.22\)%. Find \(d\).
Answer/Explanation
Ans
(a) \(0.345\) (\(34.5\)%)
(b) \(P(2 300 < X < 3 300) =0.645\)
P(both)= (0.645)^{2}=0.416
(c) d = \($ 3 325\) ( \($ 3 330\) to \(3\) s.f.) (Accept $\(3325.07\))
Question
[with GDC]
A company manufactures television sets. They claim that the lifetime of a set is normally distributed with a mean of 80 months and standard deviation of 8 months.
(a) What proportion of television sets break down in less than \(72\) months?
(b) (i) Calculate the proportion of sets with a lifetime between \(72\) and \(90\) months.
(ii) Illustrate this proportion by a sketch of a normal distribution curve.
(c) If a set breaks down in less than \(x\) months, the company replace it free of charge.
They replace \(4\)% of the sets. Find the value of \(x\).
Answer/Explanation
Ans
\(X\sim N (80,8^{2})\)
(a) \(P(X < 72) = 0.159\)
(b) (i) \(P(72 < X < 90) = 0.736\)
(ii) 
(c) \(x\) =\( 66.0\) months
Question
[without GDC]
A random variable \(X\) is distributed normally with a mean of \(100\) and a variance of \(100\).
(a) Find the value of \(X\) that is \(1.12\) standard deviations above the mean.
(b) Find the value of \(X\) that is \(1.12\) standard deviations below the mean.
Answer/Explanation
Ans
\(\sigma =10, 1.12\times 10=11.2\)
(a) \(100 + 11.2 = 111.2\)
(b) \(100 – 11.2 = 88.8\)
Question
[without GDC]
The heights of trees in a forest are normally distributed with mean height \(17\) metres. One tree is selected at random. The probability that a selected tree has a height greater than \(24\) metres is \(0.06\).
(a) Find the probability that the tree selected has a height less than \(24\) metres.
(b) The probability that the tree has a height less than \(D\) metres is \(0.06\). Find \(D\).
(c) A woodcutter randomly selects \(200\) trees. Find the expected number of trees whose height lies between \(17\) metres and \(24\) metres.
Answer/Explanation
Ans
(a) \(p = 0.94\)
(b) \(D = 10\)
(c) \(P(17 < H < 24) = 0.44\)
\(E(trees) = 200 × 0.44= 88\)
Question
[with GDC]
In a country called Tallopia, the height of adults is normally distributed with a mean of \(187.5\) cm and a standard deviation of \(9.5\) cm.
(a) What percentage of adults in Tallopia have a height greater than \(197\) cm?
(b) A standard doorway in Tallopia is designed so that \(99\)% of adults have a space of at least \(17\) cm over their heads when going through a doorway. Find the height of a standard doorway in Tallopia. Give your answer to the nearest cm.
Answer/Explanation
Ans
(a) \(P (H > 197) = 0.159 = 15.9\)%
(b) \(99\)% of heights under \(209.6 = 210\) cm (\(3\) sf)
Height of standard doorway = \(210 + 17 = 227\) cm
Question
[with GDC]
The heights of boys at a particular school follow a normal distribution with a standard deviation of \(5\) cm. The probability of a boy being shorter than \(153\) cm is \(0.705\).
(a) Calculate the mean height of the boys.
(b) Find the probability of a boy being taller than \(156\) cm.
Answer/Explanation
Ans
(a) \(P(H < 153) = 0.705\)
Standardizing \(\frac{153-\mu }{5}=0.5388…\)
\(\mu =150.30…= 150\) (to \(3\)sf)
(b) \(0.128\)
Question
[with GDC]
The scores of a test given to students are normally distributed with a mean of \(21.80\)% of the students have scores less than \(23.7\).
(a) Find the standard deviation of the scores.
A student is chosen at random. This student has the same probability of having a score less than \(25.4\) as having a score greater than \(b\).
(b) (i) Find the probability the student has a score less than \(25.4\).
(ii) Find the value of \(b\).
Answer/Explanation
Ans
(a) \(0.84…=\frac{23.7-21}{\sigma }\Rightarrow \sigma =3.21\)
(b) (i) \(P(X < 25.4) = 0.915\)
(ii) \(b=21-4.4\Rightarrow b=16.6\)
Question
[with GDC]
The heights of certain flowers follow a normal distribution. It is known that \(20\)% of these flowers have a height less than \(3\)cm and \(10\)% have a height greater than \(8\) cm.
Find the value of the mean \(μ\) and the standard deviation \(σ\).
Answer/Explanation
Ans
\(X\sim N(\mu ,\sigma ^{2})\),
\(\frac{3-\mu }{\sigma }=0.8416, \frac{8-\mu }{\sigma }=1.282\)
\(3-\mu =-0.8416\sigma\)
\(8-\mu =1.282\sigma\)
\(\sigma =2.35, \mu =4.99\)
Question
[with GDC]
The speeds of cars at a certain point on a straight road are normally distributed with mean \(μ\) and standard deviation \(σ\). \(15\) % of the cars travelled at speeds greater than \(90 \ km \ h^{-1}\) and \(12\) % of them at speeds less than \(40\ km\ h^{-1}\). Find \(μ\) and \(σ\).
Answer/Explanation
Ans
\(P(X > 90) = 0.15\) and \(P(X < 40) = 0.12\)
\(1.036=\frac{90-\mu }{\sigma},-1.175=\frac{40-\mu }{\sigma }\)
\(\mu =66.6, \sigma =22.6\)
Question
[with GDC]
A box contains a large number of biscuits. The weights of biscuits are normally distributed with mean \(7\) g and standard deviation \(0.5\) g.
(a) One biscuit is chosen at random from the box. Find the probability that this biscuit
(i) weighs less than \(8\) g; (ii) weighs between \(6\) g and \(8\) g.
(b) Five percent of the biscuits in the box weigh less than \(d\) grams.
(i) Complete the following normal distribution diagram, to represent this information, by indicating \(d\), and shading the appropriate region.
(ii) Find the value of \(d\).
(c) The weights of biscuits in another box are normally distributed with mean \(μ\) and standard deviation \(0.5\) g. It is known that \(20\)% of the biscuits in this second box weigh less than \(5\) g. Find the value of \(μ\).
Answer/Explanation
Ans
\(X\sim N (7,0.5^{2})\)
(a) (i) \(P(X < 8) = 0.977\) (ii) \(P(6 < X < 8) = 0.95\)
(b) (i) 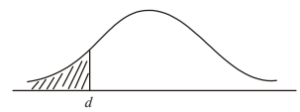
(ii) \(d = 6.18\)
(c) \(Y\sim N(\mu ,0.5^{2}), P(Y<5)=0.2\)
\(\frac{5-\mu }{0.5}=-0.8416 \mu =5.42\)
Question
[with GDC]
The lifespan of a particular species of insect is normally distributed with a mean of \(57\) hours and a standard deviation of \(4.4\) hours.
(a) The probability that the lifespan of an insect of this species lies between \(55\) and \(60\) hours is represented by the shaded area in the following diagram. This diagram represents the standard normal curve.
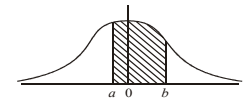
(i) Write down the values of \(a\) and \(b\).
(ii) Find the probability that the lifespan of an insect of this species is
(a) more than \(55\) hours; (b) between \(55\) and \(60\) hours.
(b) \(90\)% of the insects die after \(t\) hours.
(i) Represent this information on a standard normal curve diagram, similar to the one given in part (a), indicating clearly the area representing \(90\)%.
(ii) Find the value of \(t\).
Answer/Explanation
Ans
(a) Let \(X\) be the lifespan in hours, \(X\sim N(57, 4.4^{2})\)
(i) \(a = –0.455\) (\(3\) sf) b = \(0.682\) (\(3\) sf)
(ii) (a) P \((X > 55)\) = \(0.675\) (b) \(P(55\leq X\leq 60)=0.428\) (\(3\) sf)
(b) \(90\)% have died \(\Rightarrow\) shaded area = \(0.9\)
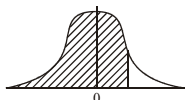
\(t = 62.6\) hours
Question
[with GDC]
The graph shows a normal curve for the random variable X, with mean μ and standard deviation σ.

It is known that \(p (X > 12) = 0.1\).
(a) The shaded region \(A\) is the region under the curve where \(x > 12\). Write down the area of the shaded region \(A\).
It is also known that \(p (X < 8) = 0.1\).
(b) Find the value of \(μ\), explaining your method in full.
(c) Show that \(σ = 1.56\) to an accuracy of three significant figures.
(d) Find \(p (X < 11)\).
Answer/Explanation
Ans
(a) Area \(A = 0.1\)
(b) EITHER Since \(p(X\geq 12)= p(X\leq 8)\),
then \(8\) and \(12\) are symmetrical about the mean.
Thus mean = \(\frac{8+12}{2}=10\)
OR
\(\frac{12-\mu }{\sigma }=\frac{\mu -8}{\sigma }\Rightarrow 12-\mu =\mu -8\Rightarrow \mu =10\)
(c) \(\left ( \frac{12-10}{\sigma } \right )=1.282\)
\(\sigma =\frac{2}{}1.282 =1.56 (3 sf)\)
(d) \(0.739 (3 sf)\)
Question
[with GDC]
The weights of chickens for sale in a shop are normally distributed with mean \(2.5\) kg and standard deviation \(0.3\) kg.
(a) A chicken is chosen at random.
(i) Find the probability that it weighs less than \(2\) kg.
(ii) Find the probability that it weighs more than \(2.8\) kg.
(iii) In the diagram below, shade the areas that represent the probabilities from parts (i) and (ii).
(iv) Find the probability that it weighs between \(2\) kg and \(2.8\) kg (\(4\)sf).
(b) A customer buys 10 chickens.
(i) Find the probability that all \(10\) chickens weigh between \(2\) kg and \(2.8\) kg.
(ii) Find the probability that at least \(7\) of the chickens weigh between \(2\) kg and \(2.8\) kg.
Answer/Explanation
Ans
\(W\sim N(2.5, 0.3^{2})\)
(a) (i) \(0.048\) (ii) \(0.159\)
(iii) 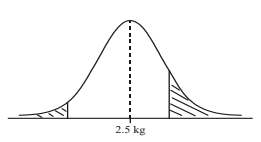
(iv) \(P = 0.7936\)
(b) (i) \(X\sim B(10, 0.7935…)\)
\(P(X=10)=(0.7935…)^{10}\) OR \(P(X = 10) = 0.0990 (3 sf)\)
(ii) \(X\sim B(10, 0.7935…)\)
\(P(X \geq 7) = 0.867\)
Question
[with GDC]
Bags of cement are labelled \(25\) kg. The bags are filled by machine and the actual weights are normally distributed with mean \(25.7\) kg and standard deviation \(0.50\) kg.
(a) What is the probability a bag selected at random will weigh less than \(25.0\) kg?
In order to reduce the number of underweight bags (bags weighing less than \(25\) kg) to \(2.5\)% of the total, the mean is increased without changing the standard deviation.
(b) Show that the increased mean is \(26.0\) kg.
It is decided to purchase a more accurate machine for filling the bags. The requirements for this machine are that only \(2.5\)% of bags be under \(25\) kg and that only \(2.5\)% of bags be over \(26\) kg.
(c) Calculate the mean and standard deviation that satisfy these requirements.
Answer/Explanation
Ans
(a) \(P(W < 25) = 0.0808\)
(b) \(\mu = 25.98 = 26.0\) (\(3\) sf)
(c) Clearly, by symmetry \(\mu = 25.5\)
\(\frac{25.0-25.5}{\sigma }=-1.96\Rightarrow 0.5=1.96\sigma \Rightarrow \sigma =0.255\) kg
Question
[with GDC]
In a large school, the heights of all fourteen-year-old students are measured.
The heights of the girls are normally distributed with mean \(155\)cm and standard deviation \(10\)cm.
The heights of the boys are normally distributed with mean \(160\)cm and standard deviation \(12\)cm.
(a) Find the probability that a girl is taller than \(170\) cm.
(b) Given that \(10\)% of the girls are shorter than \(x\) cm, find \(x\).
(c) Given that \(90\)% of the boys have heights between \(q\) cm and \(r\) cm where \(q\) and \(r\) are symmetrical about \(160\) cm, and \(q < r\), find the value of \(q\) and of \(r\).
In the group of fourteen-year-old students, \(60\)% are girls and \(40\)% are boys.
The probability that a girl is taller than \(170\) cm was found in part (a).
The probability that a boy is taller than \(170\) cm is \(0.202\).
A fourteen-year-old student is selected at random.
(d) Calculate the probability that the student is taller than \(170\) cm.
(e) Given that the student is taller than \(170\) cm, what is the probability the student is a girl?
Answer/Explanation
Ans
Girls’height \(G\sim N(155,10^{2}), Boys ‘height B\sim N(160,12^{2})\)
(a) \(P(G > 170) = 0.0668\)
(b) \(x = 142\)
(c) \(r = 180 q = 140\)
(d) \(P(H > 170 ) = 0.60\times 0.0668+0.40\times 0.202=0.12088=0.121 (3 sf)\)
(e) \(P(F|H>170)=\frac{0.60\times 0.0668}{0.121}=0.332\)