Question
Consider the function f ( x ) = ax3 + bx2 + cx + d, where x ∈ R and a, b, c , d ∈ R.
(i) Write down an expression for f ′( x ).
(ii) Hence, given that f –1 does not exist, show that b2 – 3ac > 0 . [4]
Consider the function g ( x ) \(\frac{1}{2}\) x3 – 3x2 + 6x – 8 , where x ∈ R.
Show that g–1 exists.
g ( x ) can be written in the form p ( x – 2 )3 + q , where p , q ∈ R. Find the value of p and the value of q .
Hence find g–1 ( x ). [8]
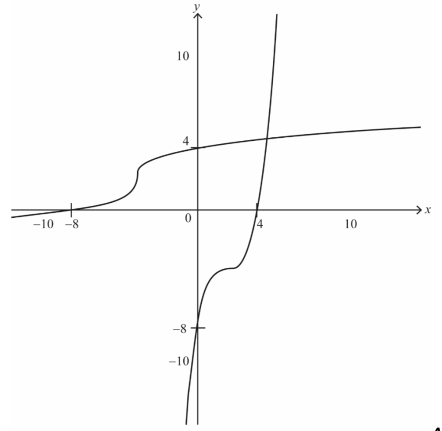
The graph of y = g ( x ) may be obtained by transforming the graph of y = x3 using a sequence of three transformations.
State each of the transformations in the order in which they are applied. [3]
Sketch the graphs of y = g ( x ) and y = g–1 ( x ) on the same set of axes, indicating the points where each graph crosses the coordinate axes. [5]
Answer/Explanation
Ans:
- (a) (i) f'(x)=\(3ax^{2}\)+2bx+c
- (a) (ii)
- \(since f^{-1}\)dose not exist , there must be two turning points
- (f(x)= 0)has more than one solutin
- using the disriminat Δ >0
- \(4b^{2}-12ac>0\)
- \(b^{2}\)-3ac>0
- (b) (i)
- METHOD 1
- \(b^{2}-3ac=(-3)^{2}-3\times \frac{1}{2}\times 6\) = 9-9 = 0
- hence g-1 exists
- METHOD 2
- g'(x)= \(\frac{3}{2}x^{2}-6x+6\)
- \(\Delta = (-6)^{2}-4\times \frac{3}{2}\times 6\)
- Δ = 36 -36 = 0 ⇒ there is (only) one point with gradient of 0 and this must be a point of inflexion (since g (x ) is a cubic.)
hence g-1 exists
- (b) (ii)
- p= \(\frac{1}{2}\)
- \((x-2)^{3}=x^{3}-6x^{2}\)+12x=8
- \(\frac{1}{2}(x^{3}-6x^{3}+12x-8)\)= \(\frac{1}{2}x^{3}-3x^{2}+6x-4\)
- g(x)=\(\frac{1}{2}(x-2)^{3}-4\)
- (b) (iii)
- x= \(\frac{1}{2}(y-2)^{3}-4\)
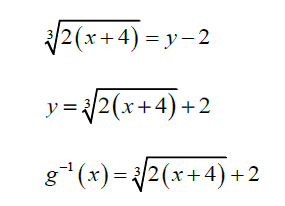
- (c)
- translation through \(\begin{pmatrix}
2\\
0
\end{pmatrix}\) - EITHER
- a stretch scale factor \(\frac{1}{2}\) parallel to the y-axis then a translation through \((_{-4}^{0})\)
- OR
- a translation through \((_{-8}^{0})\) then a stretch scale factor \(\frac{1}{2}\) parallel to the y-axis
- translation through \(\begin{pmatrix}
- (d)
Question
The acceleration, a ms-2 , of a particle moving in a horizontal line at time t seconds, t ≥ 0 , is given by a = – (1+v) where v ms-1 is the particle’s velocity and v > -1.
At t = 0 , the particle is at a fixed origin O and has initial velocity v0 ms-1 .
(a) By solving an appropriate differential equation, show that the particle’s velocity at time t is given by v ( t ) = (1 + v0) e-t – 1 . [6]
(b) Initially at O, the particle moves in the positive direction until it reaches its maximum displacement from O. The particle then returns to O.
Let s metres represent the particle’s displacement from O and smax its maximum displacement from O.
(i) Show that the time T taken for the particle to reach smax satisfies the equation eT = 1 + v0 .
(ii) By solving an appropriate differential equation and using the result from part (b) (i), find an expression for smax in terms of v0 . [7]
Let v (T – k) represent the particle’s velocity k seconds before it reaches smax , where v (T – k) = (1 + v0) e-(T – k) – 1 .
(c) By using the result to part (b) (i), show that v (T – k) = ek – 1 . [2]
Similarly, let v (T + k) represent the particle’s velocity k seconds after it reaches smax .
(d) Deduce a similar expression for v (T + k) in terms of k . [2]
(e) Hence, show that v (T – k) + v (T + k) ≥ 0 . [3]
Answer/Explanation
Ans:
(a) Since $a=\frac{\text{d}v}{\text{d}t}$, and $a=-\left(1+v\right)$, we have
$$\begin{eqnarray}
\frac{\text{d}v}{\text{d}t} = -1-v \nonumber \\
\frac{\text{d}v}{\text{d}t}+v = -1.
\end{eqnarray}$$
Let $\text{I}\left(x\right)=\text{e}^{\int 1 \text{d}t}=\text{e}^t$.<br>
Then, we have
$$\begin{eqnarray}
\frac{\text{d}}{\text{d}t}\left(v\text{e}^t\right) = -\text{e}^t \nonumber \\
v\text{e}^t = -\int\text{e}^t \text{d}t \nonumber \\
v\text{e}^t = -\text{e}^t+c \nonumber \\
v = c\text{e}^{-t}-1.
\end{eqnarray}$$
Since $v=v_0$ when $t=0$, we have $c=1+v_0$, i.e., $v=\left(1+v_0\right)\text{e}^{-t}-1$.<br>
(b)(i) At $s_{\text{max}}$, $t=T$, i.e., we have
$$\begin{eqnarray}
v\left(T\right) = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T}-1 = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T} = 1 \nonumber \\
1+v_0 = \text{e}^T.
\end{eqnarray}$$
(b)(ii) Since $\frac{\text{d}s}{\text{d}t}=\left(1+v_0\right)\text{e}^{-t}-1$, integrating both sides with respect to $t$, we have
$$\begin{eqnarray}
s &=& \int\left(1+v_0\right)\text{e}^{-t}-1\text{d}t \nonumber \\
&=& -\left(1+v_0\right)\text{e}^{-t}-t+c.
\end{eqnarray}$$
When $t=0$, $s=0$, i.e.,
$$\begin{eqnarray}
0 = -\left(1+v_0\right)+c \nonumber \\
c = \left(1+v_0\right).
\end{eqnarray}$$
Thus, $s=\left(1+v_0\right)-\left(1+v_0\right)\text{e}^{-t}-t$.<br>
Since from (b)(i) we have $1+v_0=\text{e}^T$, $T=\ln\left(1+v_0\right)$, i.e., $s_{\text{max}}=v_0-\ln \left(1+v_0\right)$.<br>
(c) Since $\text{e}^T=1+v_0$, we have $\left(1+v_0\right)\text{e}^{-T}=1$, i.e.,
$$\begin{eqnarray}
v\left(T-k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T-k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^k-1 \nonumber \\
&=& \text{e}^k-1.
\end{eqnarray}$$
(d) Similarly, as in (c),
$$\begin{eqnarray}
v\left(T+k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T+k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^{-k}-1.
\end{eqnarray}$$
(e)
$$\begin{eqnarray}
v\left(T-k\right)+v\left(T+k\right) &=& \text{e}^k-1+\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^k+\text{e}^{-k}-2 \nonumber \\
&=& \frac{\text{e}^{2k}-2\text{e}^k+1}{\text{e}^k} \nonumber \\
&=& \frac{\left(\text{e}^k-1\right)^2}{\text{e}^k} \geq 0.
\end{eqnarray}$$
Question
Consider the function f defined by f (x) = ln (x2 – 16) for x > 4 .
The following diagram shows part of the graph of f which crosses the x-axis at point A, with
coordinates ( a , 0 ). The line L is the tangent to the graph of f at the point B.
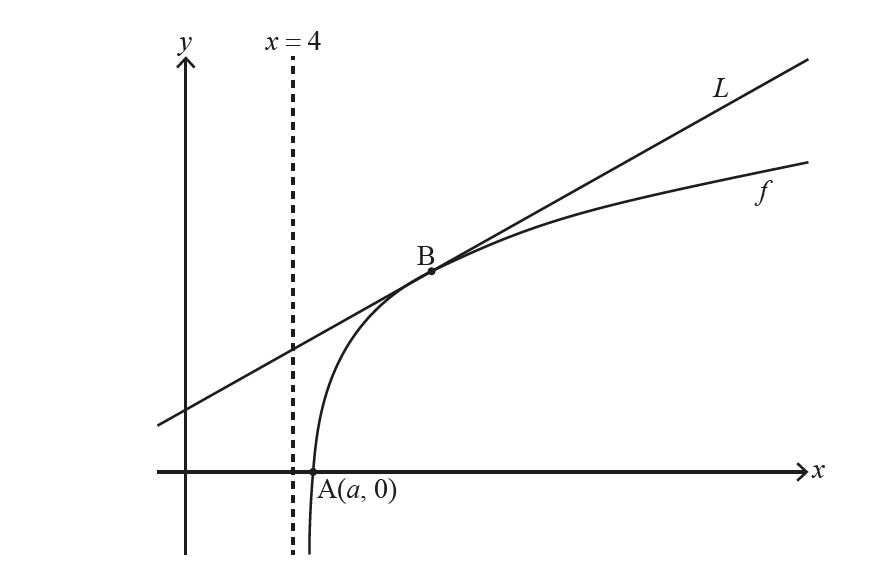
(a) Find the exact value of a . [3]
(b) Given that the gradient of L is \(\frac{1}{3}\) , find the x-coordinate of B. [6]
Answer/Explanation
Ans:
(a) When f(x)=0, we have
ln(x2−16)=0
x2−16=1
x=±√17
However, since x>4, we have x=√17
(b) Differentiating f(x) with respect to x, we have f′(x)= \(\frac{2x}{x^2-16}\)
At B, f′(x)=\(\frac{1}{3}\) , i.e., we have
x2−16=6x
x2−6x−16=0
(x+2)(x−8)=0.
Thus, x=−2 (reject) or x=8.
Question
Using the definition of a derivative as \(f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(x + h) – f(x)}}{h}} \right)\) , show that the derivative of \(\frac{1}{{2x + 1}}{\text{ is }}\frac{{ – 2}}{{{{(2x + 1)}^2}}}\).[4]
Prove by induction that the \({n^{{\text{th}}}}\) derivative of \({(2x + 1)^{ – 1}}\) is \({( – 1)^n}\frac{{{2^n}n!}}{{{{(2x + 1)}^{n + 1}}}}\).[9]
Answer/Explanation
Markscheme
let \(f(x) = \frac{1}{{2x + 1}}\) and using the result \(f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(x + h) – f(x)}}{h}} \right)\)
\(f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{\frac{1}{{2(x + h) + 1}} – \frac{1}{{2x + 1}}}}{h}} \right)\) M1A1
\( \Rightarrow f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{[2x + 1] – [2(x + h) + 1]}}{{h[2(x + h) + 1][2x + 1]}}} \right)\) A1
\( \Rightarrow f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{ – 2}}{{[2(x + h) + 1][2x + 1]}}} \right)\) A1
\( \Rightarrow f'(x) = \frac{{ – 2}}{{{{(2x + 1)}^2}}}\) AG
[4 marks]
let \(y = \frac{1}{{2x + 1}}\)
we want to prove that \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = {( – 1)^n}\frac{{{2^n}n!}}{{{{(2x + 1)}^{n + 1}}}}\)
let \(n = 1 \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = {( – 1)^1}\frac{{{2^1}1!}}{{{{(2x + 1)}^{1 + 1}}}}\) M1
\( \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – 2}}{{{{(2x + 1)}^2}}}\) which is the same result as part (a)
hence the result is true for \(n = 1\) R1
assume the result is true for \(n = k{\text{ : }}\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}} = {( – 1)^k}\frac{{{2^k}k!}}{{{{(2x + 1)}^{k + 1}}}}\) M1
\(\frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left[ {{{( – 1)}^k}\frac{{{2^k}k!}}{{{{(2x + 1)}^{k + 1}}}}} \right]\) M1
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left[ {{{( – 1)}^k}{2^k}k!{{(2x + 1)}^{ – k – 1}}} \right]\) (A1)
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = {( – 1)^k}{2^k}k!( – k – 1){(2x + 1)^{ – k – 2}} \times 2\) A1
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = {( – 1)^{k + 1}}{2^{k + 1}}(k + 1)!{(2x + 1)^{ – k – 2}}\) (A1)
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = {( – 1)^{k + 1}}\frac{{{2^{k + 1}}(k + 1)!}}{{{{(2x + 1)}^{k + 2}}}}\) A1
hence if the result is true for \(n = k\) , it is true for \(n = k + 1\)
since the result is true for \(n = 1\) , the result is proved by mathematical induction R1
Note: Only award final R1 if all the M marks have been gained.
[9 marks]
Question
A curve is defined by \(xy = {y^2} + 4\).
Show that there is no point where the tangent to the curve is horizontal.[4]
Find the coordinates of the points where the tangent to the curve is vertical.[4]
Answer/Explanation
Markscheme
\(x\frac{{{\text{d}}y}}{{{\text{d}}x}} + y = 2y\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
a horizontal tangent occurs if \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) so \(y = 0\) M1
we can see from the equation of the curve that this solution is not possible \((0 = 4)\) and so there is not a horizontal tangent R1
[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{{2y – x}}\) or equivalent with \(\frac{{{\text{d}}x}}{{{\text{d}}y}}\)
the tangent is vertical when \(2y = x\) M1
substitute into the equation to give \(2{y^2} = {y^2} + 4\) M1
\(y = \pm 2\) A1
coordinates are \((4,{\text{ }}2),{\text{ }}( – 4,{\text{ }} – 2)\) A1
[4 marks]
Total [8 marks]