Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = {x^3} – 4x + 1\) .
Expand \({(x + h)^3}\) .
Use the formula \(f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) – f(x)}}{h}\) to show that the derivative of \(f(x)\) is \(3{x^2} – 4\) .
The tangent to the curve of f at the point \({\text{P}}(1{\text{, }} – 2)\) is parallel to the tangent at a point Q. Find the coordinates of Q.
The graph of f is decreasing for \(p < x < q\) . Find the value of p and of q.
Write down the range of values for the gradient of \(f\) .
Answer/Explanation
Markscheme
attempt to expand (M1)
\({(x + h)^3} = {x^3} + 3{x^2}h + 3x{h^2} + {h^3}\) A1 N2
[2 marks]
evidence of substituting \(x + h\) (M1)
correct substitution A1
e.g. \(f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{{{(x + h)}^3} – 4(x + h) + 1 – ({x^3} – 4x + 1)}}{h}\)
simplifying A1
e.g. \(\frac{{({x^3} + 3{x^2}h + 3x{h^2} + {h^3} – 4x – 4h + 1 – {x^3} + 4x – 1)}}{h}\)
factoring out h A1
e.g. \(\frac{{h(3{x^2} + 3xh + {h^2} – 4)}}{h}\)
\(f'(x) = 3{x^2} – 4\) AG N0
[4 marks]
\(f'(1) = – 1\) (A1)
setting up an appropriate equation M1
e.g. \(3{x^2} – 4 = – 1\)
at Q, \(x = – 1,y = 4\) (Q is \(( – 1{\text{, }}4)\)) A1 A1
[4 marks]
recognizing that f is decreasing when \(f'(x) < 0\) R1
correct values for p and q (but do not accept \(p = 1.15{\text{, }}q = – 1.15\) ) A1A1 N1N1
e.g. \(p = – 1.15{\text{, }}q = 1.15\) ; \( \pm \frac{2}{{\sqrt 3 }}\) ; an interval such as \( – 1.15 \le x \le 1.15\)
[3 marks]
\(f'(x) \ge – 4\) , \(y \ge – 4\) , \(\left[ { – 4,\infty } \right[\) A2 N2
[2 marks]
Question
Consider the curve \(y = \ln (3x – 1)\) . Let P be the point on the curve where \(x = 2\) .
Write down the gradient of the curve at P.
The normal to the curve at P cuts the x-axis at R. Find the coordinates of R.
Answer/Explanation
Markscheme
gradient is \(0.6\) A2 N2
[2 marks]
at R, \(y = 0\) (seen anywhere) A1
at \(x = 2\) , \(y = \ln 5\) \(( = 1.609 \ldots )\) (A1)
gradient of normal \( = – 1.6666 \ldots \) (A1)
evidence of finding correct equation of normal A1
e.g. \(y = \ln 5 = – \frac{5}{3}(x – 2)\) , \(y = – 1.67x + c\)
\(x = 2.97\) (accept 2.96) A1
coordinates of R are (2.97,0) N3
[5 marks]
Question
Consider the curve with equation \(f(x) = p{x^2} + qx\) , where p and q are constants. The point \({\text{A}}(1{\text{, }}3)\) lies on the curve. The tangent to the curve at A has gradient \(8\). Find the value of p and of q .
Answer/Explanation
Markscheme
substituting \(x = 1\) , \(y = 3\) into \(f(x)\) (M1)
\(3 = p + q\) A1
finding derivative (M1)
\(f'(x) = 2px + q\) A1
correct substitution, \(2p + q = 8\) A1
\(p = 5\) , \(q = – 2\) A1A1 N2N2
[7 marks]
Question
Let \(f(x) = A{{\rm{e}}^{kx}} + 3\) . Part of the graph of f is shown below.
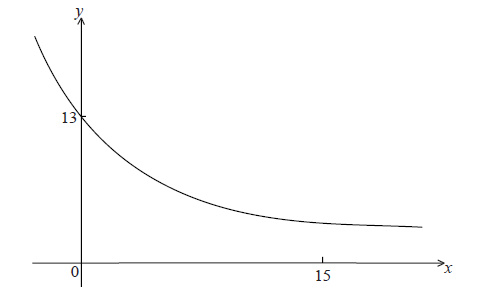
The y-intercept is at (0, 13) .
Show that \(A = 10\) .
Given that \(f(15) = 3.49\) (correct to 3 significant figures), find the value of k.
(i) Using your value of k , find \(f'(x)\) .
(ii) Hence, explain why f is a decreasing function.
(iii) Write down the equation of the horizontal asymptote of the graph f .
Let \(g(x) = – {x^2} + 12x – 24\) .
Find the area enclosed by the graphs of f and g .
Answer/Explanation
Markscheme
substituting (0, 13) into function M1
e.g. \(13 = A{{\rm{e}}^0} + 3\)
\(13 = A + 3\) A1
\(A = 10\) AG N0
[2 marks]
substituting into \(f(15) = 3.49\) A1
e.g. \(3.49 = 10{{\rm{e}}^{15k}} + 3\) , \(0.049 = {{\rm{e}}^{15k}}\)
evidence of solving equation (M1)
e.g. sketch, using \(\ln \)
\(k = – 0.201\) (accept \(\frac{{\ln 0.049}}{{15}}\) ) A1 N2
[3 marks]
(i) \(f(x) = 10{{\rm{e}}^{ – 0.201x}} + 3\)
\(f(x) = 10{{\rm{e}}^{ – 0.201x}} \times – 0.201\) \(( = – 2.01{{\rm{e}}^{ – 0.201x}})\) A1A1A1 N3
Note: Award A1 for \(10{{\rm{e}}^{ – 0.201x}}\) , A1 for \( \times – 0.201\) , A1 for the derivative of 3 is zero.
(ii) valid reason with reference to derivative R1 N1
e.g. \(f'(x) < 0\) , derivative always negative
(iii) \(y = 3\) A1 N1
[5 marks]
finding limits \(3.8953 \ldots \), \(8.6940 \ldots \) (seen anywhere) A1A1
evidence of integrating and subtracting functions (M1)
correct expression A1
e.g. \(\int_{3.90}^{8.69} {g(x) – f(x){\rm{d}}x} \) , \(\int_{3.90}^{8.69} {\left[ {\left( { – {x^2} + 12x – 24} \right) – \left( {10{{\rm{e}}^{ – 0.201x}} + 3} \right)} \right]} {\rm{d}}x\)
area \(= 19.5\) A2 N4
[6 marks]
Question
The following diagram shows a waterwheel with a bucket. The wheel rotates at a constant rate in an anticlockwise (counter-clockwise) direction.
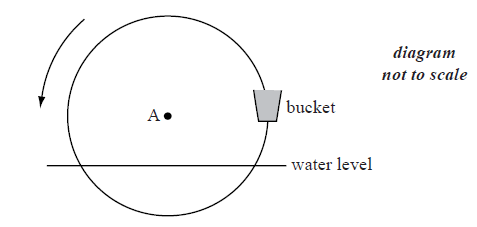
The diameter of the wheel is 8 metres. The centre of the wheel, A, is 2 metres above the water level. After t seconds, the height of the bucket above the water level is given by \(h = a\sin bt + 2\) .
Show that \(a = 4\) .
The wheel turns at a rate of one rotation every 30 seconds.
Show that \(b = \frac{\pi }{{15}}\) .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\) .
Find these values of t .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\) .
Determine whether the bucket is underwater at the second value of t .
Answer/Explanation
Markscheme
METHOD 1
evidence of recognizing the amplitude is the radius (M1)
e.g. amplitude is half the diameter
\(a = \frac{8}{2}\) A1
\(a = 4\) AG N0
METHOD 2
evidence of recognizing the maximum height (M1)
e.g. \(h = 6\) , \(a\sin bt + 2 = 6\)
correct reasoning
e.g. \(a\sin bt = 4\) and \(\sin bt\) has amplitude of 1 A1
\(a = 4\) AG N0
[2 marks]
METHOD 1
period = 30 (A1)
\(b = \frac{{2\pi }}{{30}}\) A1
\(b = \frac{\pi }{{15}}\) AG N0
METHOD 2
correct equation (A1)
e.g. \(2 = 4\sin 30b + 2\) , \(\sin 30b = 0\)
\(30b = 2\pi \) A1
\(b = \frac{\pi }{{15}}\) AG N0
[2 marks]
recognizing \(h'(t) = – 0.5\) (seen anywhere) R1
attempting to solve (M1)
e.g. sketch of \(h’\) , finding \(h’\)
correct work involving \(h’\) A2
e.g. sketch of \(h’\) showing intersection, \( – 0.5 = \frac{{4\pi }}{{15}}\cos \left( {\frac{\pi }{{15}}t} \right)\)
\(t = 10.6\) , \(t = 19.4\) A1A1 N3
[6 marks]
METHOD 1
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of substituting into h (M1)
e.g. \(h(19.4)\) , \(4\sin \frac{{19.4\pi }}{{15}} + 2\)
correct calculation A1
e.g. \(h(19.4) = – 1.19\)
correct statement A1 N0
e.g. the bucket is underwater, yes
METHOD 2
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of valid approach (M1)
e.g. solving \(h(t) = 0\) , graph showing region below x-axis
correct roots A1
e.g. \(17.5\), \(27.5\)
correct statement A1 N0
e.g. the bucket is underwater, yes
[4 marks]
Question
Let \(f(x) = \frac{{20x}}{{{{\rm{e}}^{0.3x}}}}\) , for \(0 \le x \le 20\) .
Sketch the graph of f .
(i) Write down the x-coordinate of the maximum point on the graph of f .
(ii) Write down the interval where f is increasing.
Show that \(f'(x) = \frac{{20 – 6x}}{{{{\rm{e}}^{0.3x}}}}\) .
Find the interval where the rate of change of f is increasing.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for approximately correct shape with inflexion/change of curvature, A1 for maximum skewed to the left, A1 for asymptotic behaviour to the right.
[3 marks]
(i) \(x = 3.33\) A1 N1
(ii) correct interval, with right end point \(3\frac{1}{3}\) A1A1 N2
e.g. \(0 < x \le 3.33\) , \(0 \le x < 3\frac{1}{3}\)
Note: Accept any inequalities in the right direction.
[3 marks]
valid approach (M1)
e.g. quotient rule, product rule
2 correct derivatives (must be seen in product or quotient rule) (A1)(A1)
e.g. \(20\) , \(0.3{{\rm{e}}^{0.3x}}\) or \( – 0.3{{\rm{e}}^{ – 0.3x}}\)
correct substitution into product or quotient rule A1
e.g. \(\frac{{20{{\rm{e}}^{0.3x}} – 20x(0.3){{\rm{e}}^{0.3x}}}}{{{{({{\rm{e}}^{0.3x}})}^2}}}\) , \(20{{\rm{e}}^{ – 0.3x}} + 20x( – 0.3){{\rm{e}}^{ – 0.3x}}\)
correct working A1
e.g. \(\frac{{20{{\rm{e}}^{0.3x}} – 6x{{\rm{e}}^{0.3x}}}}{{{{\rm{e}}^{0.6x}}}}\) , \(\frac{{{{\rm{e}}^{0.3x}}(20 – 20x(0.3))}}{{{{{\rm{(}}{{\rm{e}}^{0.3x}})}^2}}}\) , \({{\rm{e}}^{ – 0.3x}}(20 + 20x( – 0.3))\)
\(f'(x) = \frac{{20 – 6x}}{{{{\rm{e}}^{0.3x}}}}\) AG N0
[5 marks]
consideration of \(f’\) or \(f”\) (M1)
valid reasoning R1
e.g. sketch of \(f’\) , \(f”\) is positive, \(f” = 0\) , reference to minimum of \(f’\)
correct value \(6.6666666 \ldots \) \(\left( {6\frac{2}{3}} \right)\) (A1)
correct interval, with both endpoints A1 N3
e.g. \(6.67 < x \le 20\) , \(6\frac{2}{3} \le x < 20\)
[4 marks]
Question
Let \(f(x) = \frac{{100}}{{(1 + 50{{\rm{e}}^{ – 0.2x}})}}\) . Part of the graph of \(f\) is shown below.
Write down \(f(0)\) .
Solve \(f(x) = 95\) .
Find the range of \(f\) .
Show that \(f'(x) = \frac{{1000{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) .
Find the maximum rate of change of \(f\) .
Answer/Explanation
Markscheme
\(f(0) = \frac{{100}}{{51}}\) (exact), \(1.96\) A1 N1
[1 mark]
setting up equation (M1)
eg \(95 = \frac{{100}}{{1 + 50{{\rm{e}}^{ – 0.2x}}}}\) , sketch of graph with horizontal line at \(y = 95\)
\(x = 34.3\) A1 N2
[2 marks]
upper bound of \(y\) is \(100\) (A1)
lower bound of \(y\) is \(0\) (A1)
range is \(0 < y < 100\) A1 N3
[3 marks]
METHOD 1
setting function ready to apply the chain rule (M1)
eg \(100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 1}}\)
evidence of correct differentiation (must be substituted into chain rule) (A1)(A1)
eg \(u’ = – 100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}\) , \(v’ = (50{{\rm{e}}^{ – 0.2x}})( – 0.2)\)
correct chain rule derivative A1
eg \(f'(x) = – 100{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}(50{{\rm{e}}^{ – 0.2x}})( – 0.2)\)
correct working clearly leading to the required answer A1
eg \(f'(x) = 1000{{\rm{e}}^{ – 0.2x}}{(1 + 50{{\rm{e}}^{ – 0.2x}})^{ – 2}}\)
\(f'(x) = \frac{{1000{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) AG N0
METHOD 2
attempt to apply the quotient rule (accept reversed numerator terms) (M1)
eg \(\frac{{vu’ – uv’}}{{{v^2}}}\) , \(\frac{{uv’ – vu’}}{{{v^2}}}\)
evidence of correct differentiation inside the quotient rule (A1)(A1)
eg \(f'(x) = \frac{{(1 + 50{{\rm{e}}^{ – 0.2x}})(0) – 100(50{{\rm{e}}^{ – 0.2x}} \times – 0.2)}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) , \(\frac{{100( – 10){{\rm{e}}^{ – 0.2x}} – 0}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
any correct expression for derivative (\(0\) may not be explicitly seen) (A1)
eg \(\frac{{ – 100(50{{\rm{e}}^{ – 0.2x}} \times – 0.2)}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
correct working clearly leading to the required answer A1
eg \(f'(x) = \frac{{0 – 100( – 10){{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) , \(\frac{{ – 100( – 10){{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\)
\(f'(x) = \frac{{{\rm{1000}}{{\rm{e}}^{ – 0.2x}}}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}}}\) AG N0
[5 marks]
METHOD 1
sketch of \(f'(x)\) (A1)
eg
recognizing maximum on \(f'(x)\) (M1)
eg dot on max of sketch
finding maximum on graph of \(f'(x)\) A1
eg (\(19.6\), \(5\)) , \(x = 19.560 \ldots \)
maximum rate of increase is \(5\) A1 N2
METHOD 2
recognizing \(f”(x) = 0\) (M1)
finding any correct expression for \(f”(x) = 0\) (A1)
eg \(\frac{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^2}( – 200{{\rm{e}}^{ – 0.2x}}) – (1000{{\rm{e}}^{ – 0.2x}})(2(1 + 50{{\rm{e}}^{ – 0.2x}})( – 10{{\rm{e}}^{ – 0.2x}}))}}{{{{(1 + 50{{\rm{e}}^{ – 0.2x}})}^4}}}\)
finding \(x = 19.560 \ldots \) A1
maximum rate of increase is \(5\) A1 N2
[4 marks]
Question
Let \(f(x) = {{\rm{e}}^{\frac{x}{4}}}\) and \(g(x) = mx\) , where \(m \ge 0\) , and \( – 5 \le x \le 5\) . Let \(R\) be the region enclosed by the \(y\)-axis, the graph of \(f\) , and the graph of \(g\) .
Let \(m = 1\).
(i) Sketch the graphs of \(f\) and \(g\) on the same axes.
(ii) Find the area of \(R\) .
Find the area of \(R\) .
Consider all values of \(m\) such that the graphs of \(f\) and \(g\) intersect. Find the value of \(m\) that gives the greatest value for the area of \(R\) .
Answer/Explanation
Markscheme
(i)
A1A1 N2
Notes: Award A1 for the graph of \(f\) positive, increasing and concave up.
Award A1 for graph of \(g\) increasing and linear with \(y\)-intercept of \(0\).
Penalize one mark if domain is not [\( – 5\), \(5\)] and/or if \(f\) and \(g\) do not intersect in the first quadrant.
[2 marks]
(ii)
attempt to find intersection of the graphs of \(f\) and \(g\) (M1)
eg \({{\rm{e}}^{\frac{x}{4}}} = x\)
\(x = 1.42961 \ldots \) A1
valid attempt to find area of \(R\) (M1)
eg \(\int {(x – {{\rm{e}}^{\frac{x}{4}}}} ){\rm{d}}x\) , \(\int_0^1 {(g – f)} \) , \(\int {(f – g)} \)
area \( = 0.697\) A2 N3
[5 marks]
attempt to find intersection of the graphs of \(f\) and \(g\) (M1)
eg \({{\rm{e}}^{\frac{x}{4}}} = x\)
\(x = 1.42961 \ldots \) A1
valid attempt to find area of \(R\) (M1)
eg \(\int {(x – {{\rm{e}}^{\frac{x}{4}}}} ){\rm{d}}x\) , \(\int_0^1 {(g – f)} \) , \(\int {(f – g)} \)
area \( = 0.697\) A2 N3
[5 marks]
recognize that area of \(R\) is a maximum at point of tangency (R1)
eg \(m = f'(x)\)
equating functions (M1)
eg \(f(x) = g(x)\) , \({{\rm{e}}^{\frac{x}{4}}} = mx\)
\(f'(x) = \frac{1}{4}{{\rm{e}}^{\frac{x}{4}}}\) (A1)
equating gradients (A1)
eg \(f'(x) = g'(x)\) , \(\frac{1}{4}{{\rm{e}}^{\frac{x}{4}}} = m\)
attempt to solve system of two equations for \(x\) (M1)
eg \(\frac{1}{4}{{\rm{e}}^{\frac{x}{4}}} \times x = {{\rm{e}}^{\frac{x}{4}}}\)
\(x = 4\) (A1)
attempt to find \(m\) (M1)
eg \(f'(4)\) , \(\frac{1}{4}{{\rm{e}}^{\frac{4}{4}}}\)
\(m = \frac{1}{4}e\) (exact), \(0.680\) A1 N3
[8 marks]
Question
Consider the graph of the semicircle given by \(f(x) = \sqrt {6x – {x^2}} \), for \(0 \leqslant x \leqslant 6\). A rectangle \(\rm{PQRS}\) is drawn with upper vertices \(\rm{R}\) and \(\rm{S}\) on the graph of \(f\), and \(\rm{PQ}\) on the \(x\)-axis, as shown in the following diagram.
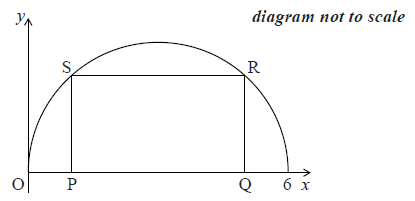
Let \({\text{OP}} = x\).
(i) Find \({\text{PQ}}\), giving your answer in terms of \(x\).
(ii) Hence, write down an expression for the area of the rectangle, giving your answer in terms of \(x\).
Find the rate of change of area when \(x = 2\).
The area is decreasing for \(a < x < b\). Find the value of \(a\) and of \(b\).
Answer/Explanation
Markscheme
(i) valid approach (may be seen on diagram) (M1)
eg \({\text{Q}}\) to \(6\) is \(x\)
\({\text{PQ}} = 6 – 2x\) A1 N2
(ii) \(A = (6 – 2x)\sqrt {6x – {x^2}} \) A1 N1
[3 marks]
recognising \(\frac{{{\text{d}}A}}{{{\text{d}}x}}\) at \(x = 2\) needed (must be the derivative of area) (M1)
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = – \frac{{7\sqrt 2 }}{2},{\text{ }} – 4.95\) A1 N2
[2 marks]
\(a = 0.879{\text{ }}b = 3\) A1A1 N2
[4 marks]
Question
The population of deer in an enclosed game reserve is modelled by the function \(P(t) = 210\sin (0.5t – 2.6) + 990\), where \(t\) is in months, and \(t = 1\) corresponds to 1 January 2014.
Find the number of deer in the reserve on 1 May 2014.
Find the rate of change of the deer population on 1 May 2014.
Interpret the answer to part (i) with reference to the deer population size on 1 May 2014.
Answer/Explanation
Markscheme
\(t = 5\) (A1)
correct substitution into formula (A1)
eg \(210\sin (0.5 \times 5 – 2.6) + 990,{\text{ }}P(5)\)
\(969.034982 \ldots \)
969 (deer) (must be an integer) A1 N3
[3 marks]
evidence of considering derivative (M1)
eg \(P’\)
\(104.475\)
\(104\) (deer per month) A1 N2
[2 marks]
(the deer population size is) increasing A1 N1
[1 mark]
Question
Let \(f(x) = \frac{{\ln (4x)}}{x}\) for \(0 < x \le 5\).
Points \({\text{P}}(0.25,{\text{ }}0)\) and \(Q\) are on the curve of \(f\). The tangent to the curve of \(f\) at \(P\) is perpendicular to the tangent at \(Q\). Find the coordinates of \(Q\).
Answer/Explanation
Markscheme
recognizing that the gradient of tangent is the derivative (M1)
eg\(\;\;\;f’\)
finding the gradient of \(f\) at \(P\) (A1)
eg\(\;\;\;f'(0.25) = 16\)
evidence of taking negative reciprocal of their gradient at \(P\) (M1)
eg\(\;\;\;\frac{{ – 1}}{m},{\text{ }} – \frac{1}{{f'(0.25)}}\)
equating derivatives M1
eg\(\;\;\;f'(x) = \frac{{ – 1}}{{16}},{\text{ }}f’ = – \frac{1}{m},{\text{ }}\frac{{x\left( {\frac{1}{x}} \right) – \ln (4x)}}{{{x^2}}} = 16\)
finding the \(x\)-coordinate of \(Q\), \(x = 0.700750\)
\(x = 0.701\) A1 N3
attempt to substitute their \(x\) into \(f\) to find the \(y\)-coordinate of \(Q\) (M1)
eg\(\;\;\;f(0.7)\)
\(y = 1.47083\)
\(y = 1.47\) A1 N2
[7 marks]
Question
Let \(f(x) = \frac{1}{{x – 1}} + 2\), for \(x > 1\).
Let \(g(x) = a{e^{ – x}} + b\), for \(x \geqslant 1\). The graphs of \(f\) and \(g\) have the same horizontal asymptote.
Write down the equation of the horizontal asymptote of the graph of \(f\).
Find \(f'(x)\).
Write down the value of \(b\).
Given that \(g'(1) = – e\), find the value of \(a\).
There is a value of \(x\), for \(1 < x < 4\), for which the graphs of \(f\) and \(g\) have the same gradient. Find this gradient.
Answer/Explanation
Markscheme
\(y = 2\) (correct equation only) A2 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\({(x – 1)^{ – 1}} + 2,{\text{ }}f'(x) = \frac{{0(x – 1) – 1}}{{{{(x – 1)}^2}}}\)
\( – {(x – 1)^{ – 2}},{\text{ }}f'(x) = \frac{{ – 1}}{{{{(x – 1)}^2}}}\) A1 N2
[2 marks]
correct equation for the asymptote of \(g\)
eg\(\,\,\,\,\,\)\(y = b\) (A1)
\(b = 2\) A1 N2
[2 marks]
correct derivative of g (seen anywhere) (A2)
eg\(\,\,\,\,\,\)\(g'(x) = – a{{\text{e}}^{ – x}}\)
correct equation (A1)
eg\(\,\,\,\,\,\)\( – {\text{e}} = – a{{\text{e}}^{ – 1}}\)
7.38905
\(a = {{\text{e}}^2}{\text{ }}({\text{exact}}),{\text{ }}7.39\) A1 N2
[4 marks]
attempt to equate their derivatives (M1)
eg\(\,\,\,\,\,\)\(f'(x) = g'(x),{\text{ }}\frac{{ – 1}}{{{{(x – 1)}^2}}} = – a{{\text{e}}^{ – x}}\)
valid attempt to solve their equation (M1)
eg\(\,\,\,\,\,\)correct value outside the domain of \(f\) such as 0.522 or 4.51,
correct solution (may be seen in sketch) (A1)
eg\(\,\,\,\,\,\)\(x = 2,{\text{ }}(2,{\text{ }} – 1)\)
gradient is \( – 1\) A1 N3
[4 marks]
Question
The following diagram shows the graph of \(f(x) = a\sin bx + c\), for \(0 \leqslant x \leqslant 12\).
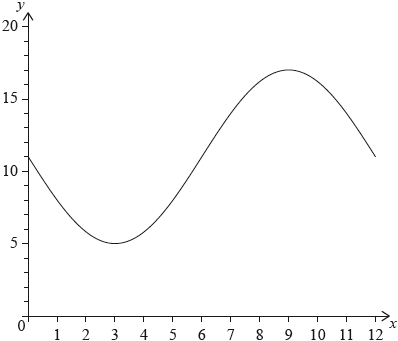
The graph of \(f\) has a minimum point at \((3,{\text{ }}5)\) and a maximum point at \((9,{\text{ }}17)\).
The graph of \(g\) is obtained from the graph of \(f\) by a translation of \(\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)\). The maximum point on the graph of \(g\) has coordinates \((11.5,{\text{ }}17)\).
The graph of \(g\) changes from concave-up to concave-down when \(x = w\).
(i) Find the value of \(c\).
(ii) Show that \(b = \frac{\pi }{6}\).
(iii) Find the value of \(a\).
(i) Write down the value of \(k\).
(ii) Find \(g(x)\).
(i) Find \(w\).
(ii) Hence or otherwise, find the maximum positive rate of change of \(g\).
Answer/Explanation
Markscheme
(i) valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{5 + 17}}{2}\)
\(c = 11\) A1 N2
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)period is 12, per \( = \frac{{2\pi }}{b},{\text{ }}9 – 3\)
\(b = \frac{{2\pi }}{{12}}\) A1
\(b = \frac{\pi }{6}\) AG N0
(iii) METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11\), substitution of points
\(a = – 6\) A1 N2
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{17 – 5}}{2}\), amplitude is 6
\(a = – 6\) A1 N2
[6 marks]
(i) \(k = 2.5\) A1 N1
(ii) \(g(x) = – 6\sin \left( {\frac{\pi }{6}(x – 2.5)} \right) + 11\) A2 N2
[3 marks]
(i) METHOD 1 Using \(g\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(g”(x) = 0\), sketch, coordinates of max/min on \({g’}\)
\(w = 8.5\) (exact) A1 N2
METHOD 2 Using \(f\)
recognizing that a point of inflexion is required M1
eg\(\,\,\,\,\,\)sketch, recognizing change in concavity
evidence of valid approach involving translation (M1)
eg\(\,\,\,\,\,\)\(x = w – k\), sketch, \(6 + 2.5\)
\(w = 8.5\) (exact) A1 N2
(ii) valid approach involving the derivative of \(g\) or \(f\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(g'(w),{\text{ }} – \pi \cos \left( {\frac{\pi }{6}x} \right)\), max on derivative, sketch of derivative
attempt to find max value on derivative M1
eg\(\,\,\,\,\,\)\( – \pi \cos \left( {\frac{\pi }{6}(8.5 – 2.5)} \right),{\text{ }}f'(6)\), dot on max of sketch
3.14159
max rate of change \( = \pi \) (exact), 3.14 A1 N2
[6 marks]
Question
Let \(f(x) = – 0.5{x^4} + 3{x^2} + 2x\). The following diagram shows part of the graph of \(f\).
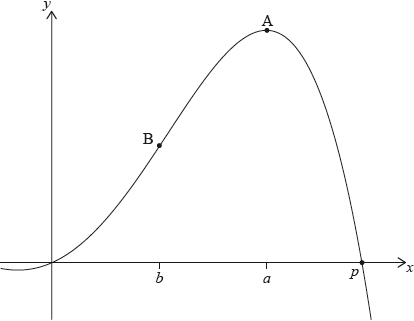
There are \(x\)-intercepts at \(x = 0\) and at \(x = p\). There is a maximum at A where \(x = a\), and a point of inflexion at B where \(x = b\).
Find the value of \(p\).
Write down the coordinates of A.
Write down the rate of change of \(f\) at A.
Find the coordinates of B.
Find the the rate of change of \(f\) at B.
Let \(R\) be the region enclosed by the graph of \(f\) , the \(x\)-axis, the line \(x = b\) and the line \(x = a\). The region \(R\) is rotated 360° about the \(x\)-axis. Find the volume of the solid formed.
Answer/Explanation
Markscheme
evidence of valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }}y = 0\)
2.73205
\(p = 2.73\) A1 N2
[2 marks]
1.87938, 8.11721
\((1.88,{\text{ }}8.12)\) A2 N2
[2 marks]
rate of change is 0 (do not accept decimals) A1 N1
[1 marks]
METHOD 1 (using GDC)
valid approach M1
eg\(\,\,\,\,\,\)\(f’’ = 0\), max/min on \(f’,{\text{ }}x = – 1\)
sketch of either \(f’\) or \(f’’\), with max/min or root (respectively) (A1)
\(x = 1\) A1 N1
Substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
METHOD 2 (analytical)
\(f’’ = – 6{x^2} + 6\) A1
setting \(f’’ = 0\) (M1)
\(x = 1\) A1 N1
substituting their \(x\) value into \(f\) (M1)
eg\(\,\,\,\,\,\)\(f(1)\)
\(y = 4.5\) A1 N1
[4 marks]
recognizing rate of change is \(f’\) (M1)
eg\(\,\,\,\,\,\)\(y’,{\text{ }}f’(1)\)
rate of change is 6 A1 N2
[3 marks]
attempt to substitute either limits or the function into formula (M1)
involving \({f^2}\) (accept absence of \(\pi \) and/or \({\text{d}}x\))
eg\(\,\,\,\,\,\)\(\pi \int {{{( – 0.5{x^4} + 3{x^2} + 2x)}^2}{\text{d}}x,{\text{ }}\int_1^{1.88} {{f^2}} } \)
128.890
\({\text{volume}} = 129\) A2 N3
[3 marks]
Question
Let \(f(x) = 4x – {{\rm{e}}^{x – 2}} – 3\) , for \(0 \le x \le 5\) .
Find the x-intercepts of the graph of f .
On the grid below, sketch the graph of f .
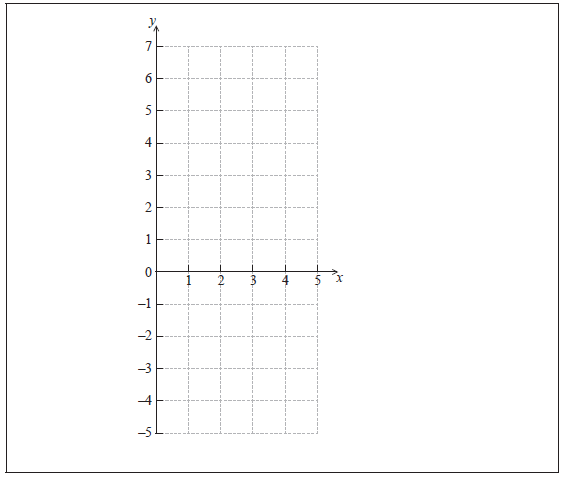
Write down the gradient of the graph of f at \(x = 3\) .
Answer/Explanation
Markscheme
intercepts when \(f(x) = 0\) M1
(0.827, 0) (4.78, 0) (accept \(x = 0.827\), \(x = 4.78\) ) A1A1 N3
[3 marks]
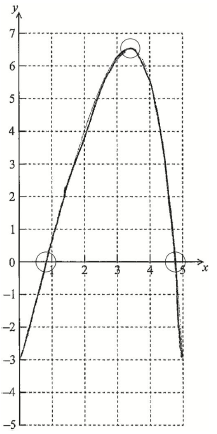A1A1A1 N3
Note: Award A1 for maximum point in circle, A1 for x-intercepts in circles, A1 for correct shape (y approximately greater than \( – 3.14\)).
[3 marks]
gradient is 1.28 A1 N1
[1 mark]