Question
Let \(f(x) = 1 + {{\text{e}}^{ – x}}\) and \(g(x) = 2x + b\), for \(x \in \mathbb{R}\), where \(b\) is a constant.
Find \((g \circ f)(x)\). [2]
Given that \(\mathop {\lim }\limits_{x \to + \infty } (g \circ f)(x) = – 3\), find the value of \(b\). [4]
Answer/Explanation
Markscheme
attempt to form composite (M1)
eg\(\,\,\,\,\,\)\(g(1 + {{\text{e}}^{ – x}})\)
correct function A1 N2
eg\(\,\,\,\,\,\)\((g \circ f)(x) = 2 + b + 2{{\text{e}}^{ – x}},{\text{ }}2(1 + {{\text{e}}^{ – x}}) + b\)
[2 marks]
evidence of \(\mathop {\lim }\limits_{x \to \infty } (2 + b + 2{{\text{e}}^{ – x}}) = 2 + b + \mathop {\lim }\limits_{x \to \infty } (2{{\text{e}}^{ – x}})\) (M1)
eg\(\,\,\,\,\,\)\(2 + b + 2{{\text{e}}^{ – \infty }}\), graph with horizontal asymptote when \(x \to \infty \)
Note: Award M0 if candidate clearly has incorrect limit, such as \(x \to 0,{\text{ }}{{\text{e}}^\infty },{\text{ }}2{{\text{e}}^0}\).
evidence that \({{\text{e}}^{ – x}} \to 0\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\mathop {\lim }\limits_{x \to \infty } ({{\text{e}}^{ – x}}) = 0,{\text{ }}1 + {{\text{e}}^{ – x}} \to 1,{\text{ }}2(1) + b = – 3,{\text{ }}{{\text{e}}^{{\text{large negative number}}}} \to 0\), graph of \(y = {{\text{e}}^{ – x}}\) or
\(y = 2{{\text{e}}^{ – x}}\) with asymptote \(y = 0\), graph of composite function with asymptote \(y = – 3\)
correct working (A1)
eg\(\,\,\,\,\,\)\(2 + b = – 3\)
\(b = – 5\) A1 N2
[4 marks]
Question
The graph of the function \(f\) is shown below
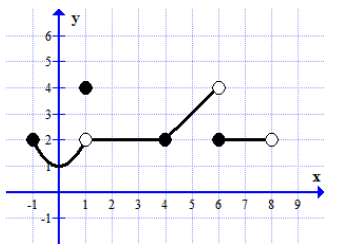
- Write down the domain and the range of the function.
Domain of \(f\) : Range of \(f \): - Complete the following table of values
\(f (-1)=\) \(f (1)=\) \(f (4)=\) \(f (6)=\) \(f (8)=\) - Complete the following table of limits (if there exist)
\(\lim_{x\rightarrow 1^{-}}f(x)=\) \(\lim_{x\rightarrow 1^{+}}f(x)=\) \(\lim_{x\rightarrow 1}f(x)=\) \(\lim_{x\rightarrow 4^{-}}f(x)=\) \(\lim_{x\rightarrow 4^{+}}f(x)=\) \(\lim_{x\rightarrow 4}f(x)=\) \(\lim_{x\rightarrow 6^{-}}f(x)=\) \(\lim_{x\rightarrow 6^{+}}f(x)=\) \(\lim_{x\rightarrow 6}f(x)=\) - Determine whether the functions is continuous at \(x = 4 , x =1, x= 6\) .
Is \(f\) continuous at \(x = 4\) YES, since \(\lim_{x\rightarrow 4}f(x)=2\) and \(f(4)=2\) Is \(f\) continuous at \(x = 1\) Is \(f\) continuous at \(x = 6\)
Answer/Explanation
Ans:
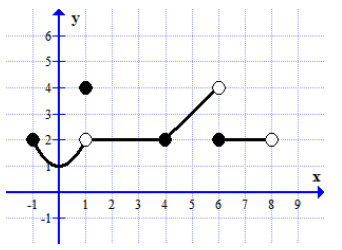
Domain of \(f\) : \(x \in [-1,8]\)
Range of \(f \): \(y \in [1,4]\) \(f (-1)=2\) \(f (1)=4\) \(f (4)=2\) \(f (6)=2\) \(f (8)=\) not defined - Complete the following table of limits (if there exist)
\(\lim_{x\rightarrow 1^{-}}f(x)=2\) \(\lim_{x\rightarrow 1^{+}}f(x)=2\) \(\lim_{x\rightarrow 1}f(x)=2\) \(\lim_{x\rightarrow 4^{-}}f(x)=2\) \(\lim_{x\rightarrow 4^{+}}f(x)=2\) \(\lim_{x\rightarrow 4}f(x)=2\) \(\lim_{x\rightarrow 6^{-}}f(x)=4\) \(\lim_{x\rightarrow 6^{+}}f(x)=2\) \(\lim_{x\rightarrow 6}f(x)\) does not exist. - Determine whether the functions is continuous at \(x = 4 , x =1, x= 6\) .
Is \(f\) continuous at \(x = 4\) YES, since \(\lim_{x\rightarrow 4}f(x)=2\) and \(f(4)=2\) Is \(f\) continuous at \(x = 1\) NO, since \(\lim_{x\rightarrow 1}f(x)=2\) and \(f(1)=4 \space 2 \ne 4.\) Is \(f\) continuous at \(x = 6\) NO, since \(\lim_{x\rightarrow 6}f(x)\) does not exist.
Question
- Write down the values of the following limits
\(\lim_{x\to 3} \frac{x+3}{x-2}=\) \(\lim_{x\to +\infty} \frac{x+3}{x-2}=\) \(\lim_{x\to -\infty} \frac{x+3}{x-2}=\) - Investigate whether each of the following side limits is \(+\infty\) or \(-\infty\)
\(\lim_{x\to 2^{+}} \frac{x+3}{x-2}=\) \(\lim_{x\to 2^{-}} \frac{x+3}{x-2}=\) \(\lim_{x\to 2^{+}} \frac{x-3}{x-2}=\) \(\lim_{x\to 2^{-}} \frac{x-3}{x-2}=\)
Answer/Explanation
Ans:
\(\lim_{x\to 3} \frac{x+3}{x-2}=6\) \(\lim_{x\to +\infty} \frac{x+3}{x-2}=1\) \(\lim_{x\to -\infty} \frac{x+3}{x-2}=-1\) \(\lim_{x\to 2^{+}} \frac{x+3}{x-2}=+\infty\) \(\lim_{x\to 2^{-}} \frac{x+3}{x-2}=-\infty\) \(\lim_{x\to 2^{+}} \frac{x-3}{x-2}=-\infty\) \(\lim_{x\to 2^{-}} \frac{x-3}{x-2}=+\infty\)
