Question
Consider the curve with equation \( y=(2x-1)e^{kx}, \) where \(x\in \mathbb{R} \) and \(k\in \mathbb{Q}\)
The tangent to the curve at the point where x = 1 is parallel to the line \(y=5e^kx\)
Find the value of k .
Answer/Explanation
Ans:

Question
Let y = \(\frac{Inx}{x^{4}}\) for x > 0.
(a) Show that \(\frac{dy}{dx}= \frac{1-4Inx}{x^{5}}\)
Consider the function defined by f (x) \(\frac{Inx}{x^{4}}\) = for x> 0 and its graph y = f (x) .
(b) The graph of f has a horizontal tangent at point P. Find the coordinates of P. [5]
(c) Given that f ” (x) = \(\frac{20Lnx-9}{x^{6}}\) show that P is a local maximum point. [3]
(d) Solve f (x) > 0 for x > 0. [2]
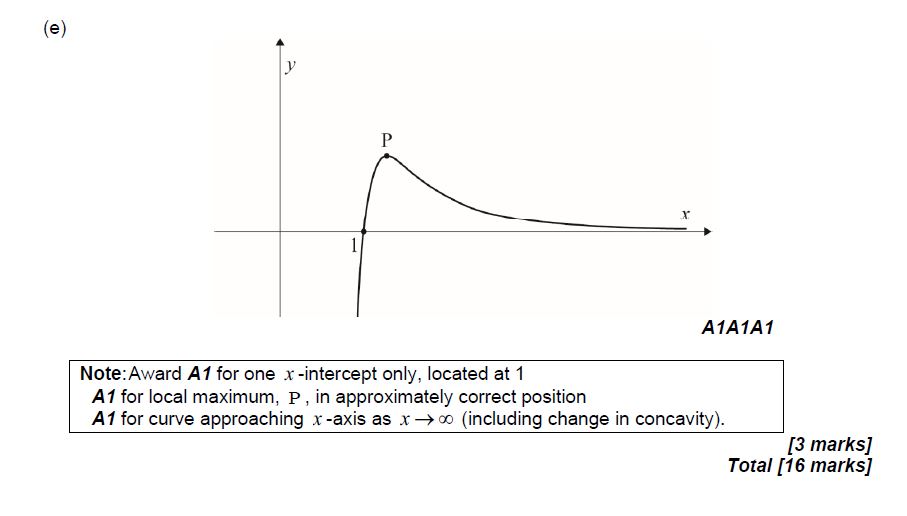
(e) Sketch the graph of f , showing clearly the value of the x-intercept and the approximate position of point P. [3]
Answer/Explanation
Ans



Question
Consider the functions f (x) = -(x – h)2 + 2k and g(x) = e x-2 + k where h , k ∈ R.
(a) Find f ′(x). [1]
The graphs of f and g have a common tangent at x = 3
(b) Show that h + = \(\frac{e+6}{2}\) [3]
(c) Hence, show that k = \(e+ \frac{e^{2}}{4}\) [3]
Answer/Explanation
Ans
(a) f ‘( x) = −2( x − h)
(b)
\(g'(x) = e^{x-2}\) or \(g'(3)=e^{3-2}= e\)
Now given that f and g has common tangent at x=3
Hence \(f'(3) =g'(3)\)
\(f'(x)= -2 (x-h)\) or
\(f'(3)=-2(3-h)\)
Hence
\(-2(3-h) =e\)
or
\(h = \frac{e+6}{2}\)
(c )
\(f(3)=g(3) \) as function has common tangent at \(x=3 \) , hence both function has common values as well
\(-(3-h)^2 +2k= e^{3-2}+k\)
putting the value of e from part (b)
\(-(3-\frac{e+6}{2})^2 + 2k = e+k\)
or
\(k = e+ \frac{e^{2}}{4}\)
Question
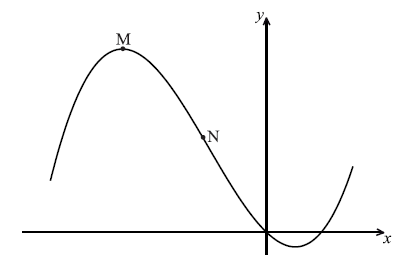
Consider \(f(x) = \frac{1}{3}{x^3} + 2{x^2} – 5x\) . Part of the graph of f is shown below. There is a maximum point at M, and a point of inflexion at N.
Find \(f'(x)\) .[3]
Find the x-coordinate of M.[4]
Find the x-coordinate of N.[3]
The line L is the tangent to the curve of f at \((3{\text{, }}12)\). Find the equation of L in the form \(y = ax + b\) .[4]
Answer/Explanation
Markscheme
\(f'(x) = {x^2} + 4x – 5\) A1A1A1 N3
[3 marks]
evidence of attempting to solve \(f'(x) = 0\) (M1)
evidence of correct working A1
e.g. \((x + 5)(x – 1)\) , \(\frac{{ – 4 \pm \sqrt {16 + 20} }}{2}\) , sketch
\(x = – 5\), \(x = 1\) (A1)
so \(x = – 5\) A1 N2
[4 marks]
METHOD 1
\(f”(x) = 2x + 4\) (may be seen later) A1
evidence of setting second derivative = 0 (M1)
e.g. \(2x + 4 = 0\)
\(x = – 2\) A1 N2
METHOD 2
evidence of use of symmetry (M1)
e.g. midpoint of max/min, reference to shape of cubic
correct calculation A1
e.g. \(\frac{{ – 5 + 1}}{2}\)
\(x = – 2\) A1 N2
[3 marks]
attempting to find the value of the derivative when \(x = 3\) (M1)
\(f'(3) = 16\) A1
valid approach to finding the equation of a line M1
e.g. \(y – 12 = 16(x – 3)\) , \(12 = 16 \times 3 + b\)
\(y = 16x – 36\) A1 N2
[4 marks]
Question
Let \(f(x) = \sqrt x \) . Line L is the normal to the graph of f at the point (4, 2) .
In the diagram below, the shaded region R is bounded by the x-axis, the graph of f and the line L .
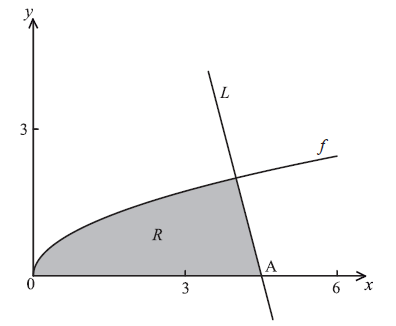
Show that the equation of L is \(y = – 4x + 18\) .
Point A is the x-intercept of L . Find the x-coordinate of A.
Find an expression for the area of R .
The region R is rotated \(360^\circ \) about the x-axis. Find the volume of the solid formed, giving your answer in terms of \(\pi \) .
Answer/Explanation
Markscheme
finding derivative (A1)
e.g. \(f'(x) = \frac{1}{2}{x^{\frac{1}{2}}},\frac{{1}}{{2\sqrt x }}\)
correct value of derivative or its negative reciprocal (seen anywhere) A1
e.g. \(\frac{1}{{2\sqrt 4 }}\) , \(\frac{1}{4}\)
gradient of normal = \(\frac{1}{{{\text{gradient of tangent}}}}\) (seen anywhere) A1
e.g. \( – \frac{1}{{f'(4)}} = – 4\) , \( – 2\sqrt x \)
substituting into equation of line (for normal) M1
e.g. \(y – 2 = – 4(x – 4)\)
\(y = – 4x + 18\) AG N0
[4 marks]
recognition that \(y = 0\) at A (M1)
e.g. \( – 4x + 18 = 0\)
\(x = \frac{{18}}{4}\) \(\left( { = \frac{9}{2}} \right)\) A1 N2
[2 marks]
splitting into two appropriate parts (areas and/or integrals) (M1)
correct expression for area of R A2 N3
e.g. area of R = \(\int_0^4 {\sqrt x } {\rm{d}}x + \int_4^{4.5} {( – 4x + 18){\rm{d}}x} \) , \(\int_0^4 {\sqrt x } {\rm{d}}x + \frac{1}{2} \times 0.5 \times 2\) (triangle)
Note: Award A1 if dx is missing.
[3 marks]
correct expression for the volume from \(x = 0\) to \(x = 4\) (A1)
e.g. \(V = \int_0^4 {\pi \left[ {f{{(x)}^2}} \right]} {\rm{d}}x\) , \({\int_0^4 {\pi \sqrt x } ^2}{\rm{d}}x\) , \(\int_0^4 {\pi x{\rm{d}}x} \)
\(V = \left[ {\frac{1}{2}\pi {x^2}} \right]_0^4\) A1
\(V = \pi \left( {\frac{1}{2} \times 16 – \frac{1}{2} \times 0} \right)\) (A1)
\(V = 8\pi \) A1
finding the volume from \(x = 4\) to \(x = 4.5\)
EITHER
recognizing a cone (M1)
e.g. \(V = \frac{1}{3}\pi {r^2}h\)
\(V = \frac{1}{3}\pi {(2)^2} \times \frac{1}{2}\) (A1)
\( = \frac{{2\pi }}{3}\) A1
total volume is \(8\pi + \frac{2}{3}\pi \) \(\left( { = \frac{{26}}{3}\pi } \right)\) A1 N4
OR
\(V = \pi \int_4^{4.5} {{{( – 4x + 18)}^2}{\rm{d}}x} \) (M1)
\( = \int_4^{4.5} {\pi (16{x^2} – 144x + 324){\rm{d}}x} \)
\( = \pi \left[ {\frac{{16}}{3}{x^3} – 72{x^2} + 324x} \right]_4^{4.5}\) A1
\( = \frac{{2\pi }}{3}\) A1
total volume is \(8\pi + \frac{2}{3}\pi \) \(\left( { = \frac{{26}}{3}\pi } \right)\) A1 N4
[8 marks]