Question
Let \(f(x) = {{\rm{e}}^x}(1 – {x^2})\) .
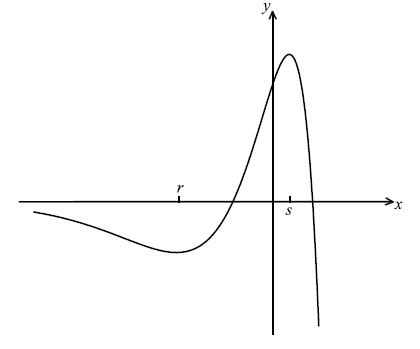
Part of the graph of \(y = f(x)\), for \( – 6 \le x \le 2\) , is shown below. The x-coordinates of the local minimum and maximum points are r and s respectively.
Show that \(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) .
Write down the equation of the horizontal asymptote.
Write down the value of r and of s.
Let L be the normal to the curve of f at \({\text{P}}(0{\text{, }}1)\) . Show that L has equation \(x + y = 1\) .
Let R be the region enclosed by the curve \(y = f(x)\) and the line L.
(i) Find an expression for the area of R.
(ii) Calculate the area of R.
Answer/Explanation
Markscheme
evidence of using the product rule M1
\(f'(x) = {{\rm{e}}^x}(1 – {x^2}) + {{\rm{e}}^x}( – 2x)\) A1A1
Note: Award A1 for \({{\rm{e}}^x}(1 – {x^2})\) , A1 for \({{\rm{e}}^x}( – 2x)\) .
\(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) AG N0
[3 marks]
\(y = 0\) A1 N1
[1 mark]
at the local maximum or minimum point
\(f'(x) = 0\) \(({{\rm{e}}^x}(1 – 2x – {x^2}) = 0)\) (M1)
\( \Rightarrow 1 – 2x – {x^2} = 0\) (M1)
\(r = – 2.41\) \(s = 0.414\) A1A1 N2N2
[4 marks]
\(f'(0) = 1\) A1
gradient of the normal \(= – 1\) A1
evidence of substituting into an equation for a straight line (M1)
correct substitution A1
e.g. \(y – 1 = – 1(x – 0)\) , \(y – 1 = – x\) , \(y = – x + 1\)
\(x + y = 1\) AG N0
[4 marks]
(i) intersection points at \(x = 0\) and \(x = 1\) (may be seen as the limits) (A1)
approach involving subtraction and integrals (M1)
fully correct expression A2 N4
e.g. \(\int_0^1 {\left( {{{\rm{e}}^x}(1 – {x^2}) – (1 – x)} \right)} {\rm{d}}x\) , \(\int_0^1 {f(x){\rm{d}}x – \int_0^1 {(1 – x){\rm{d}}x} } \)
(ii) area \(R = 0.5\) A1 N1
[5 marks]
Question
Let \(f(x) = {{\rm{e}}^{2x}}\cos x\) , \( – 1 \le x \le 2\) .
Show that \(f'(x) = {{\rm{e}}^{2x}}(2\cos x – \sin x)\) .
Let the line L be the normal to the curve of f at \(x = 0\) .
Find the equation of L .
The graph of f and the line L intersect at the point (0, 1) and at a second point P.
(i) Find the x-coordinate of P.
(ii) Find the area of the region enclosed by the graph of f and the line L .
Answer/Explanation
Markscheme
correctly finding the derivative of \({{\rm{e}}^{2x}}\) , i.e. \(2{{\rm{e}}^{2x}}\) A1
correctly finding the derivative of \(\cos x\) , i.e. \( – \sin x\) A1
evidence of using the product rule, seen anywhere M1
e.g. \(f'(x) = 2{{\rm{e}}^{2x}}\cos x – {{\rm{e}}^{2x}}\sin x\)
\(f'(x) = 2{{\rm{e}}^{2x}}(2\cos x – \sin x)\) AG N0
[3 marks]
evidence of finding \(f(0) = 1\) , seen anywhere A1
attempt to find the gradient of f (M1)
e.g. substituting \(x = 0\) into \(f'(x)\)
value of the gradient of f A1
e.g. \(f'(0) = 2\) , equation of tangent is \(y = 2x + 1\)
gradient of normal \( = – \frac{1}{2}\) (A1)
\(y – 1 = – \frac{1}{2}x\left( {y = – \frac{1}{2}x + 1} \right)\) A1 N3
[5 marks]
(i) evidence of equating correct functions M1
e.g. \({{\rm{e}}^{2x}}\cos x = – \frac{1}{2}x + 1\) , sketch showing intersection of graphs
\(x = 1.56\) A1 N1
(ii) evidence of approach involving subtraction of integrals/areas (M1)
e.g. \(\int {\left[ {f(x) – g(x)} \right]} {\rm{d}}x\) , \(\int {f(x)} {\rm{d}}x – {\text{area under trapezium}}\)
fully correct integral expression A2
e.g. \(\int_0^{1.56} {\left[ {{{\rm{e}}^{2x}}\cos x – \left( { – \frac{1}{2}x + 1} \right)} \right]} {\rm{d}}x\) , \(\int_0^{1.56} {{{\rm{e}}^{2x}}\cos x} {\rm{d}}x – 0.951 \ldots \)
\({\rm{area}} = 3.28\) A1 N2
[6 marks]
Question
Consider the curve \(y = \ln (3x – 1)\) . Let P be the point on the curve where \(x = 2\) .
Write down the gradient of the curve at P.
The normal to the curve at P cuts the x-axis at R. Find the coordinates of R.
Answer/Explanation
Markscheme
gradient is \(0.6\) A2 N2
[2 marks]
at R, \(y = 0\) (seen anywhere) A1
at \(x = 2\) , \(y = \ln 5\) \(( = 1.609 \ldots )\) (A1)
gradient of normal \( = – 1.6666 \ldots \) (A1)
evidence of finding correct equation of normal A1
e.g. \(y = \ln 5 = – \frac{5}{3}(x – 2)\) , \(y = – 1.67x + c\)
\(x = 2.97\) (accept 2.96) A1
coordinates of R are (2.97,0) N3
[5 marks]
Question
Consider the curve with equation \(f(x) = p{x^2} + qx\) , where p and q are constants. The point \({\text{A}}(1{\text{, }}3)\) lies on the curve. The tangent to the curve at A has gradient \(8\). Find the value of p and of q .
Answer/Explanation
Markscheme
substituting \(x = 1\) , \(y = 3\) into \(f(x)\) (M1)
\(3 = p + q\) A1
finding derivative (M1)
\(f'(x) = 2px + q\) A1
correct substitution, \(2p + q = 8\) A1
\(p = 5\) , \(q = – 2\) A1A1 N2N2
[7 marks]
Question
Let \(f(x) = \frac{{g(x)}}{{h(x)}}\), where \(g(2) = 18,{\text{ }}h(2) = 6,{\text{ }}g'(2) = 5\), and \(h'(2) = 2\). Find the equation of the normal to the graph of \(f\) at \(x = 2\).
Answer/Explanation
Markscheme
recognizing need to find \(f(2)\) or \(f'(2)\) (R1)
\(f(2) = \frac{{18}}{6}\) (seen anywhere) (A1)
correct substitution into the quotient rule (A1)
eg \(\frac{{6(5) – 18(2)}}{{{6^2}}}\)
\(f'(2) = – \frac{6}{{36}}\) A1
gradient of normal is 6 (A1)
attempt to use the point and gradient to find equation of straight line (M1)
eg \(y – f(2) = – \frac{1}{{f'(2)}}(x – 2)\)
correct equation in any form A1 N4
eg \(y – 3 = 6(x – 2),{\text{ }}y = 6x – 9\)
[7 marks]
Question
Let \(f(x) = 0.225{x^3} – 2.7x\), for \( – 3 \leqslant x \leqslant 3\). There is a local minimum point at A.
On the following grid,
Find the coordinates of A.
(i) sketch the graph of \(f\), clearly indicating the point A;
(ii) sketch the tangent to the graph of \(f\) at A.
Answer/Explanation
Markscheme
\({\text{A }}(2,{\text{ }}-3.6)\) A1A1 N2
[2 marks]
(i) (ii) 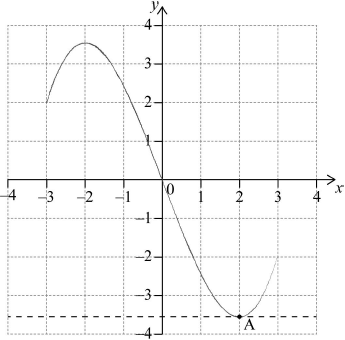 A1
A1
A1A1A1 N4
A1 N1
Notes: (i) Award A1 for correct cubic shape with correct curvature.
Only if this A1 is awarded, award the following:
A1 for passing through their point A and the origin,
A1 for endpoints,
A1 for maximum.
(ii) Award A1 for horizontal line through their A.
[5 marks]

