Question
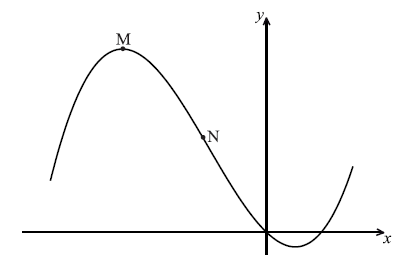
Consider \(f(x) = \frac{1}{3}{x^3} + 2{x^2} – 5x\) . Part of the graph of f is shown below. There is a maximum point at M, and a point of inflexion at N.
Find \(f'(x)\) .
Find the x-coordinate of M.
Find the x-coordinate of N.
The line L is the tangent to the curve of f at \((3{\text{, }}12)\). Find the equation of L in the form \(y = ax + b\) .
Answer/Explanation
Markscheme
\(f'(x) = {x^2} + 4x – 5\) A1A1A1 N3
[3 marks]
evidence of attempting to solve \(f'(x) = 0\) (M1)
evidence of correct working A1
e.g. \((x + 5)(x – 1)\) , \(\frac{{ – 4 \pm \sqrt {16 + 20} }}{2}\) , sketch
\(x = – 5\), \(x = 1\) (A1)
so \(x = – 5\) A1 N2
[4 marks]
METHOD 1
\(f”(x) = 2x + 4\) (may be seen later) A1
evidence of setting second derivative = 0 (M1)
e.g. \(2x + 4 = 0\)
\(x = – 2\) A1 N2
METHOD 2
evidence of use of symmetry (M1)
e.g. midpoint of max/min, reference to shape of cubic
correct calculation A1
e.g. \(\frac{{ – 5 + 1}}{2}\)
\(x = – 2\) A1 N2
[3 marks]
attempting to find the value of the derivative when \(x = 3\) (M1)
\(f'(3) = 16\) A1
valid approach to finding the equation of a line M1
e.g. \(y – 12 = 16(x – 3)\) , \(12 = 16 \times 3 + b\)
\(y = 16x – 36\) A1 N2
[4 marks]
Question
Consider \(f(x) = {x^2} + \frac{p}{x}\) , \(x \ne 0\) , where p is a constant.
Find \(f'(x)\) .
There is a minimum value of \(f(x)\) when \(x = – 2\) . Find the value of \(p\) .
Answer/Explanation
Markscheme
\(f'(x) = 2x – \frac{p}{{{x^2}}}\) A1A1 N2
Note: Award A1 for \(2x\) , A1 for \( – \frac{p}{{{x^2}}}\) .
[2 marks]
evidence of equating derivative to 0 (seen anywhere) (M1)
evidence of finding \(f'( – 2)\) (seen anywhere) (M1)
correct equation A1
e.g. \( – 4 – \frac{p}{4} = 0\) , \( – 16 – p = 0\)
\(p = – 16\) A1 N3
[4 marks]
Question
Let \(f(x) = p{x^3} + p{x^2} + qx\).
Find \(f'(x)\).
Given that \(f'(x) \geqslant 0\), show that \({p^2} \leqslant 3pq\).
Answer/Explanation
Markscheme
\(f'(x) = 3p{x^2} + 2px + q\) A2 N2
Note: Award A1 if only 1 error.
[2 marks]
evidence of discriminant (must be seen explicitly, not in quadratic formula) (M1)
eg \({b^2} – 4ac\)
correct substitution into discriminant (may be seen in inequality) A1
eg \({(2p)^2} – 4 \times 3p \times q,{\text{ }}4{p^2} – 12pq\)
\(f'(x) \geqslant 0\) then \(f’\) has two equal roots or no roots (R1)
recognizing discriminant less or equal than zero R1
eg \(\Delta \leqslant 0,{\text{ }}4{p^2} – 12pq \leqslant 0\)
correct working that clearly leads to the required answer A1
eg \({p^2} – 3pq \leqslant 0,{\text{ }}4{p^2} \leqslant 12pq\)
\({p^2} \leqslant 3pq\) AG N0
[5 marks]